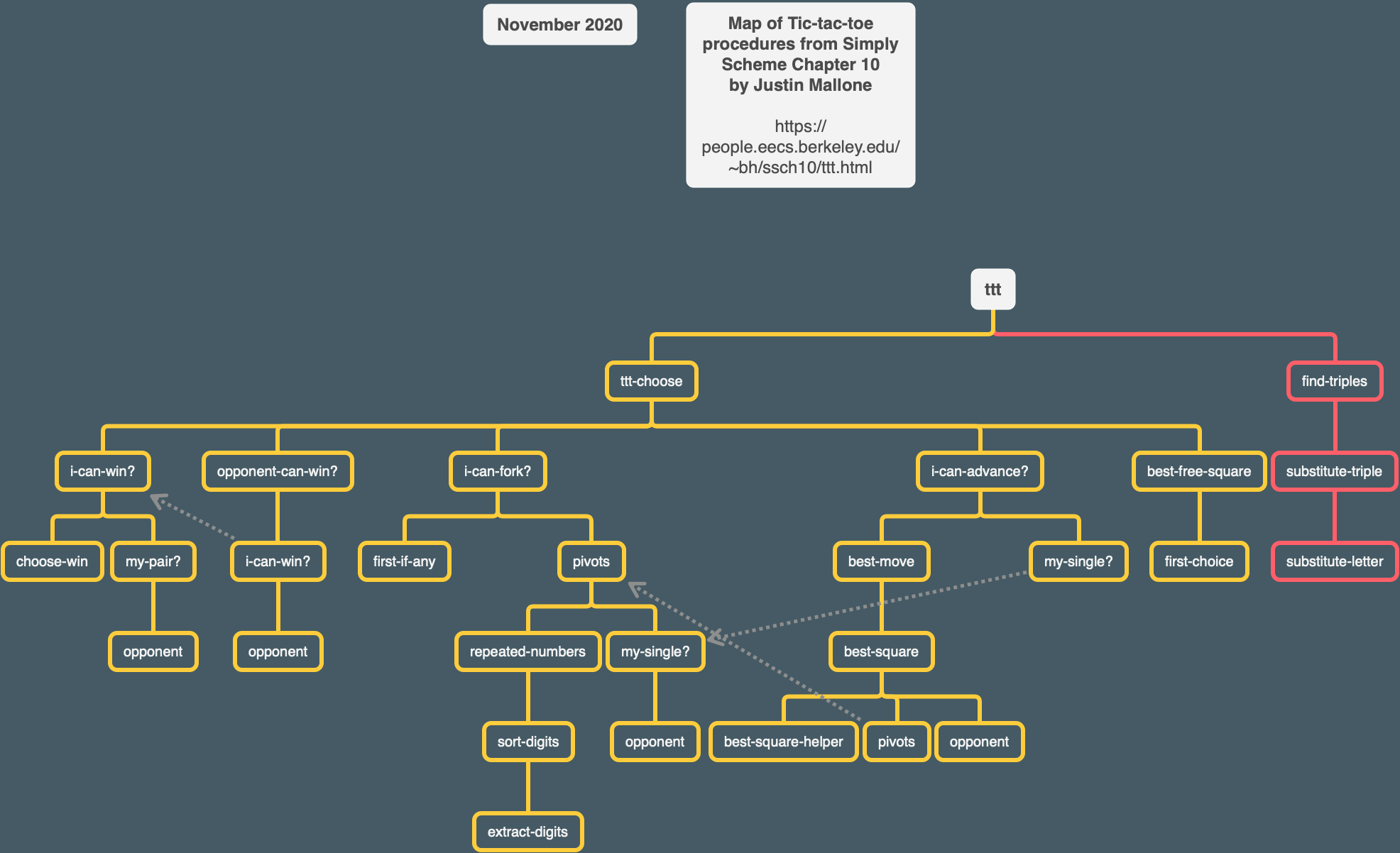
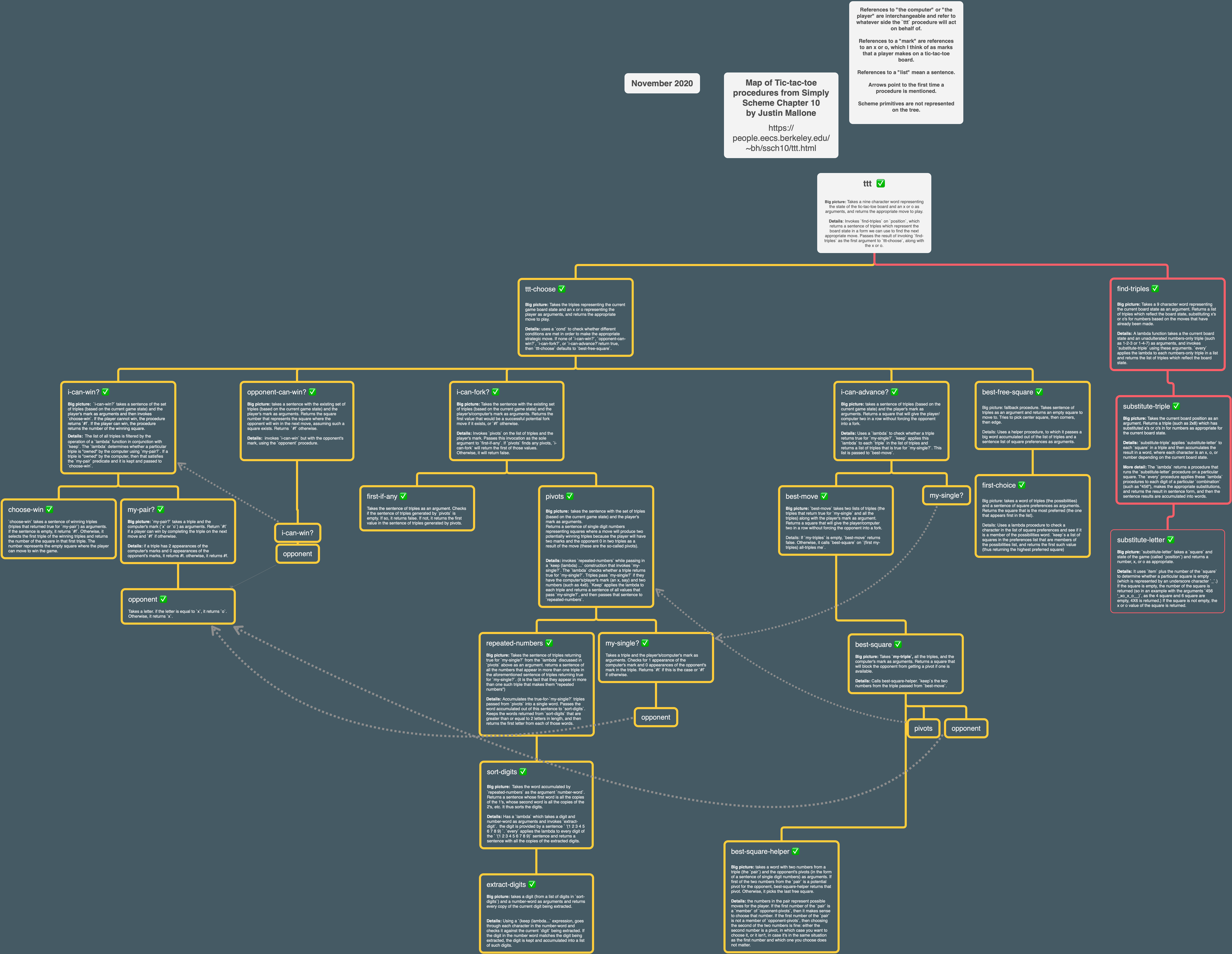
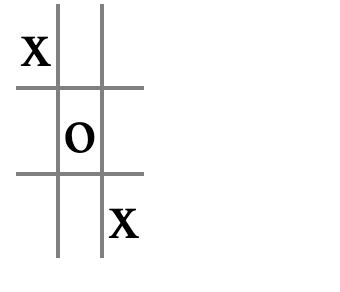Note: References to “the computer” or “the player” are interchangeable and refer to whatever side the ttt procedure will act on behalf of. References to a “mark” are references to an x or o, which I think of as marks that a player makes on a tic-tac-toe board.
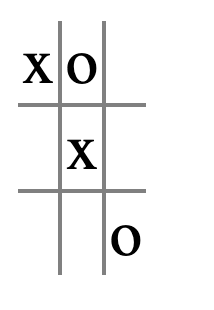
For this chapter we’re loading ttt.scm. It’s a Tic-Tac-Toe program that takes the following arguments: the current game board state (in the form of a word like '__o_xox_x, where each character corresponds to a position on the game board) and whether the computer is playing x or o.
For this chapter I quoted heavily and made comments on the quoted material as I went along.
Here’s how the board locations are numbered:
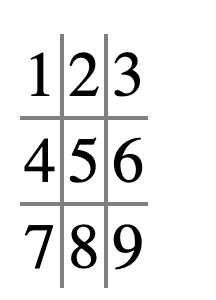
When referring to “triples” like 1-5-9 below, I’m using this numbering of the spaces.
Here’s the board state that '__o_xox_x corresponds to:
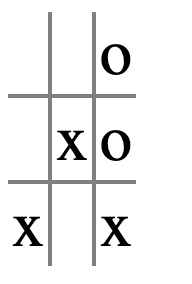
Strategy
The focus of the chapter is on strategy. Tic-tac-toe is a fairly simple game strategically – perfect play is easily doable. The book lays out the following first draft implementation of strategy:
|
1
2
3
4
5
6
7
8
9
|
(define (ttt position me) ;; first version
(cond ((i-can-win?)
(choose-winning-move))
((opponent-can-win?)
(block-opponent-win))
((i-can-win-next-time?)
(prepare-win))
(else (whatever))))
|
This lacks a bunch of detail like arguments, and is more in the vein of a pseudo-code roadmap for what we want to do.
Triples
You win tic-tac-toe by getting three of the same value (x’s or o’s) in a row, so these triples (1-5-9, 3-5-7, 1-2-3, 4-5-6, 7-8-9, 1-4-7, 2-5-8, 3-6-9) are key.
So we want to a list of triples and the current board position and put that information together somehow so that we can determine what the next move should be.
Our program will start with this sentence of all the winning combinations:
|
1
2
|
(123 456 789 147 258 369 159 357)
|
and a position word such as
_xo_x_o__; it will return a sentence of triples such as
|
1
2
|
(1xo 4x6 o89 14o xx8 o69 1x9 oxo)
|
All that’s necessary is to replace some of the numbers with
xs andos. This kind of word-by-word translation in a sentence is a good job forevery.
|
1
2
3
|
(define (find-triples position) ;; first version
(every substitute-triple '(123 456 789 147 258 369 159 357)))
|
substitute-triple, which we haven’t written yet, will take 3 digits from our list of triples and make the appropriate substitutions with the information from position. (Note that substitute-triple isn’t currently being passed position as an argument).
substitute-triple will have a procedure called substitute-letter which does the actual substitution of the letters:
|
1
2
3
|
(define (substitute-triple combination) ;; first version
(every substitute-letter combination))
|
We want triples to be words, not sentences like (2 x 8), so substitute-triple should return words:
|
1
2
3
|
(define (substitute-triple combination) ;; second version
(accumulate word (every substitute-letter combination)))
|
(This process of iterating on a program to get it closer to what we want to do is fun).
Substitute-letterknows that letter number 3 of the word that represents the board corresponds to the contents of square 3 of the board.
Hmm not currently sure how it knows that.
This means that it can just call
itemwith the given square number and the board to find out what’s in that square. If it’s empty, we return the square number itself; otherwise we return the contents of the square.
|
1
2
3
4
5
|
(define (substitute-letter square) ;; first version
(if (equal? '_ (item square position))
square
(item square position)))
|
Whoops! Do you see the problem?
|
1
2
3
|
> (substitute-letter 5)
ERROR: Variable POSITION is unbound.
|
This is the same issue I was worrying about earlier.
Using Every with Two-Argument Procedures
Our procedure only takes one argument,
square, but it needs to know the position so it can find out what’s in the given square. So here’s the realsubstitute-letter:
|
1
2
3
4
5
6
7
8
9
10
11
|
(define (substitute-letter square position)
(if (equal? '_ (item square position))
square
(item square position)))
> (substitute-letter 5 '_xo_x_o__)
X
> (substitute-letter 8 '_xo_x_o__)
8
|
Now
substitute-lettercan do its job, since it has access to the position. But we’ll have to modifysubstitute-tripleto invokesubstitute-letterwith two arguments.
Right. This is the thing I was wondering about earlier. Since substitute-triple calls substitute-letter, we’ve got to give substitute-triple access to position. Are we gonna use a lambda or let or something perhaps?
This is a little tricky. Let’s look again at the way we’re using
substitute-letterinsidesubstitute-triple:
|
1
2
3
|
(define (substitute-triple combination) ;; second version again
(accumulate word (every substitute-letter combination)))
|
By giving
substitute-letteranother argument, we have made this formerly correct procedure incorrect. The first argument toeverymust be a function of one argument, not two. This is exactly the kind of situation in whichlambdacan help us: We have a function of two arguments, and we need a function of one argument that does the same thing, but with one of the arguments fixed.
🤔 I’m not 100% sure I follow this part. Is substitute-letter only a function of one argument in the lambda below? It seems like it’s still taking two arguments.
The procedure returned by
|
1
2
|
(lambda (square) (substitute-letter square position))
|
does exactly the right thing; it takes a square as its argument and returns the contents of the position at that square.
Here’s the final version ofsubstitute-triple:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
|
(define (substitute-triple combination position)
(accumulate word
(every (lambda (square) (substitute-letter square position)) combination)))
> (substitute-triple 456 '_xo_x_o__)
"4X6"
> (substitute-triple 147 '_xo_x_o__)
"14O"
> (substitute-triple 357 '_xo_x_o__)
OXO
|
Ok so summing up in my own words so far:
substitute-letter takes a square and state of the game (called position). It uses item plus the number of the square to determine whether a particular square is empty (which is represented by an underscore character _.) If the square is empty, the number of the square is returned (so in the example with the arguments 456 '_xo_x_o__), as the 4 square is empty, 4X6 is returned.) If the square is not empty, the x or o value of the square is returned.
substitute-triple applies substitute-letter to each square in a triple and then accumulates the result in a word. The lambda returns a procedure that runs the substitute-letter procedure on a particular square. The every procedure applies these lambda procedures to each digit of a particular combination (such as “456”), and returns the result in sentence form, and then the sentence results are accumulated into words.
We’ve fixed the
substitute-letterproblem by givingsubstitute-triplean extra argument, so we’re going to have to go through the same process withfind-triples. Here’s the right version:
|
1
2
3
4
|
(define (find-triples position)
(every (lambda (comb) (substitute-triple comb position))
'(123 456 789 147 258 369 159 357)))
|
It’s the same trick.
Substitute-tripleis a procedure of two arguments. We uselambdato transform it into a procedure of one argument for use withevery.
Thinking about this issue some more…position is fixed but comb varies. Like the every will provide the lambda here with 123 as the comb and 456 and so on. And the lambda only has one formal parameter defined. I’m not sure which of those is the critical decisive factor in terms of what lets us say that the lambda is now a one-argument function but I can maybe see the idea a bit.
Wait…I was looking at how the unnamed procedure is defined (in terms of another procedure) and looking at the number of arguments the procedure inside the lambda took, rather than thinking about what arguments the lambda was taking (namely, the one parameter defined for each lambda)
We’ve now finished
find-triples, one of the most important procedures in the game.
|
1
2
3
4
|
> (find-triples '_xo_x_o__)("1XO" "4X6" O89 "14O" XX8 O69 "1X9" OXO)
> (find-triples 'x_____oxo)(X23 456 OXO X4O "25X" "36O" X5O "35O")
|
Can the Computer Win on This Move?
Finally, the computer can win if it owns any of the triples:
|
1
2
3
4
5
6
|
(define (i-can-win? triples me) ;; firstversion (not (empty? (keep (lambda (triple) (my-pair? triple me)) triples))))
> (i-can-win? '("1xo" "4x6" o89 "14o" xx8 o69 "1x9" oxo) 'x)
#T
> (i-can-win? '("1xo" "4x6" o89 "14o" xx8 o69 "1x9" oxo) 'o)
#F
|
the not (empty? part causes the procedure to return true if there are any triples the computer “owns”.
If So, in Which Square?
Suppose
i-can-win?returns#t. We then have to find the particular square that will win the game for us. This will involve a repetition of some of the same work we’ve already done:
This would keep the number from a triple that can be won on the next move. Since the number represents the fact that a square is not occupied by an x or o, then that number represents the square where a winning move can be made.
We again use
keepto find the triples with two of the computer’s letter, but this time we extract the number from the first such winning triple.
Right.
We’d like to avoid this inefficiency. As it turns out, generations of Lisp programmers have been in just this bind in the past, and so they’ve invented a kludge to get around it.
Remember we told you that everything other than#fcounts as true? We’ll take advantage of that by having a single procedure that returns the number of a winning square if one is available, or#fotherwise.
Ok that makes sense as a solution.
In Chapter 6 we called such a procedure a “semipredicate.” The kludgy part is that
condaccepts a clause containing a single expression instead of the usual two expressions; if the expression has any true value, thencondreturns that value. So we can say
where each
condclause invokes a semipredicate.
I was unclear on this point so I wound up trying to explain it at length.
So normally a cond expression looks something like this
|
1
2
3
4
5
6
7
8
9
10
|
(define (roman-value letter)
(cond (equal? letter 'i) 1)
(equal? letter 'v) 5)
(equal? letter 'x) 10)
(equal? letter 'l) 50)
(equal? letter 'c) 100)
(equal? letter 'd) 500)
(equal? letter 'm) 1000)
else 'huh?))
|
in this we see two distinct expressions – for example, (equal? letter 'i) and 1. The second expression is returned if the condition in the first expression is met.
However, earlier, in chapter 6, the book authors did give us the following warning:
Don’t get into bad habits of thinking about the appearance of
condclauses in terms of “two parentheses in a row.” That’s often the case, but not always. For example, here is a procedure that translates Scheme true or false values (#tand#f) into more human-readable wordstrueandfalse.
|
1
2
3
4
5
6
7
8
9
|
(define (truefalse value)
(cond (value 'true)
(else 'false)))
> (truefalse (= 2 (+ 1 1)))
TRUE
> (truefalse (= 5 (+ 2 2)))
FALSE
|
The meaning of (value 'true) is basically “If value is #t, return 'true.” Because Scheme defaults to treating stuff as true unless it’s false, then if value has any non-false value, truefalse will return #t. And this is accomplished inside a single set of parentheses. However, even with truefalse, there is still a separation between the thing being evaluated and the thing being returned. In other words, value is the thing that is getting evaluated for its truth value, and 'true is the thing being returned if the evaluation of value is #t.
With the proposed changes to our tic-tac-toe program, (i-can-win? triples me) will return a single value that will 1) provide the truth value that is evaluated as true or false for the purposes of the cond expression and 2) provide additional information (besides merely being true or false) when returning a true value (namely, it will return the number of the square that provides the winning move).
We then modify
i-can-win?to have the desired behavior:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
|
(define (i-can-win? triples me)
(choose-win (keep (lambda (triple) (my-pair? triple me)) triples)))
(define (choose-win winning-triples)
(if (empty? winning-triples)
#f
(keep number? (first winning-triples))))
> (i-can-win? '("1xo" "4x6" o89 "14o" xx8 o69 "1x9" oxo) 'x)
8
> (i-can-win? '("1xo" "4x6" o89 "14o" xx8 o69 "1x9" oxo) 'o)
#F
|
my-pair? takes a triple and the computer’s mark (x or o) as arguments and then determines whether a triple has 2 appearances of the computer’s marks and 0 appearances of the opponent’s marks.
i-can-win? takes the existing set of triples (based on the current game state) and the computer’s mark as arguments and then invokes choose-win. The list of all triples is filtered by the operation of a lambda function in conjunction with keep. The lambda determines whether a particular triple is “owned” by the computer using my-pair?. If a triple is “owned” by the computer, then that satisfied the my-pair predicate and it is kept and passed to choose-win.
choose-win takes a list of winning triples as arguments. If the list is empty, it returns #f. Otherwise, it keeps and returns the number that is present in the first winning triple.
Second Verse, Same as the First
Now it’s time to deal with the second possible strategy case: The computer can’t win on this move, but the opponent can win unless we block a triple right now.
(What if the computer and the opponent both have immediate winning triples? In that case, we’ve already noticed the computer’s win, and by winning the game we avoid having to think about blocking the opponent.)
Once again, we have to go through the complicated business of finding triples that have two of the opponent’s letter and none of the computer’s letter-but it’s already done!
|
1
2
3
4
5
6
7
8
|
(define (opponent-can-win? triples me) (i-can-win? triples (opponent me)))
> (opponent-can-win? '("1xo" "4x6" o89 "14o" xx8 o69 "1x9" oxo)
'x)
#F
> (opponent-can-win? '("1xo" "4x6" o89 "14o" xx8 o69 "1x9" oxo) 'o)
8
|
Is that amazing or what?
the opponent procedure returns the other mark (x or o) from whatever the computer’s mark is, and a lot of our work can work fine with either side so that saves us a lot of work.
Finding the Pivots
Pivotsshould return a sentence containing the pivot numbers. Here’s the plan. We’ll start with the triples:
|
1
2
|
(xo3 4x6 78o x47 ox8 36o xxo 3x7)
|
We
keepthe ones that have anxand two numbers:
|
1
2
|
(4x6 x47 3x7)
|
Right, these are our candidates for potentially finding pivots. And we already dealt with the 2 x’s case earlier with i-can-win?.
We mash these into one huge word:
|
1
2
|
4x6x473x7
|
We sort the digits from this word into nine “buckets,” one for each digit:
|
1
2
|
("" "" 3 44 "" 6 77 "" "")
|
We see that there are no ones or twos, one three, two fours, and so on. Now we can easily see that four and seven are the pivot squares.
Right. The repeated appearance of a number in triples where our mark appearances once indicates a pivot.
Let’s write the procedures to carry out that plan.
Pivotshas to find all the triples with one computer-owned square and two free squares, and then it has to extract the square numbers that appear in more than one triple.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
|
(define (pivots triples me)
(repeated-numbers
(keep (lambda (triple) (my-single? triple me)) triples)))
(define (my-single? triple me)
(and (= (appearances me triple) 1)
(= (appearances (opponent me) triple) 0)))
> (my-single? "4x6" 'x)
#T
> (my-single? 'xo3 'x)
#F
> (keep (lambda (triple) (my-single? triple 'x))(find-triples 'xo__x___o))
("4X6" X47 "3X7")
|
My-single?is just likemy-pair?except that it looks for one appearance of the letter instead of two.
Makes sense. And then the lambda in pivots checks if a particular triple is returns true for my-single?, and a list of triples that meet that criteria is returned to repeated-numbers for further processing.
Repeated-numberstakes a sentence of triples as its argument and has to return a sentence of all the numbers that appear in more than one triple.
|
1
2
3
4
|
(define (repeated-numbers sent)
(every first
(keep (lambda (wd) (>= (count wd) 2)) (sort-digits (accumulate word sent)))))
|
We’re going to read this procedure inside-out, starting with the
accumulateand working outward.
Why is it okay toaccumulate wordthe sentence? Suppose that a number appears in two triples. All we need to know is that number, not the particular triples through which we found it.
Right that makes sense.
Therefore, instead of writing a program to look through several triples separately, we can just as well combine the triples into one long word, keep only the digits of that word, and simply look for the ones that appear more than once.
|
1
2
3
|
> (accumulate word '("4x6" x47 "3x7"))
"4X6X473X7"
|
We now have one long word, and we’re looking for repeated digits. Since this is a hard problem, let’s start with the subproblem of finding all the copies of a particular digit.
Seems like maybe you could use appearances somehow perhaps?
|
1
2
3
4
5
6
7
8
|
(define (extract-digit desired-digit wd)
(keep (lambda (wd-digit) (equal? wd-digit desired-digit)) wd))
> (extract-digit 7 "4x6x473x7")
77
> (extract-digit 2 "4x6x473x7")
""
|
Ok so what this appears to do is check the word with the digits for the presence of a desired digit. Specifically, the lambda checks to see if a digit is in the digit-word is equaled to the desired digit. If so, it returns all instances of that digit.
Now we want a sentence where the first word is all the
1s, the second word is all the2s, etc. We could do it like this:
|
1
2
|
(se (extract-digit 1 "4x6x473x7") (extract-digit 2 "4x6x473x7")(extract-digit 3 "4x6x473x7")…)
|
that looks inelegant!
but that wouldn’t be taking advantage of the power of computers to do that sort of repetitious work for us. Instead, we’ll use
every:
|
1
2
3
4
|
(define (sort-digits number-word)
(every (lambda (digit) (extract-digit digit number-word))
'(1 2 3 4 5 6 7 8 9)))
|
So this program has a lambda which takes a digit and number-word and returns the digit the same number of times it appears in number-word. number-word is an argument from sort-digits and the digit is provided by the '(1 2 3 4 5 6 7 8 9) sentence. every applies the lambda to every digit of the '(1 2 3 4 5 6 7 8 9) sentence and returns a sentence with all the copies of the extracted digits.
Sort-digitstakes a word full of numbers and returns a sentence whose first word is all the ones, second word is all the twos, etc.[2]
|
1
2
3
4
5
|
> (sort-digits 123456789147258369159357)
(111 22 333 44 5555 66 777 88 999)
> (sort-digits "4x6x473x7")
("" "" 3 44 "" 6 77 "" "")
|
what’s with the 5 ""‘s? I thought maybe it was related to the x‘s but there are only 3 of those.
Let’s look at
repeated-numbersagain:
|
1
2
3
4
5
6
7
8
9
10
11
|
(define (repeated-numbers sent)
(every first
(keep (lambda (wd) (>= (count wd) 2)) (sort-digits (accumulate word sent)))))
> (repeated-numbers '("4x6" x47 "3x7"))
(4 7)
> (keep (lambda (wd) (>= (count wd) 2))'("" "" 3 44 "" 6 77 "" ""))
(44 77)
> (every first '(44 77))
(4 7)
|
So repeated-numbers takes a sentence of triples. It has to return a sentence of all the numbers that appear in more than one triple.
sort-digits accumulates a word from the triples and then sorts the numbers and groups instances of the same number that appear more than once together as words within a sentence.
The keep (lambda (wd)... bit keeps all the words within the sentence created by sort-digits that appear at least twice (which indicates a pivot)
Then every-first returns only the first digit of each pivot-word.
This concludes the explanation of
pivots. Remember thati-can-fork?chooses the first pivot, if any, as the computer’s move.
Taking the Offensive
Here’s the final version of
ttt-choosewith all the clauses shown:
|
1
2
3
4
5
6
7
|
(define (ttt-choose triples me)
(cond ((i-can-win? triples me))
((opponent-can-win? triples me))
((i-can-fork? triples me))
((i-can-advance? triples me))
(else (best-free-square triples))))
|
You already know about the first three possibilities.
Just as the second possibility was the “mirror image” of the first (blocking an opponent’s move of the same sort the computer just attempted), it would make sense for the fourth possibility to be blocking the creation of a fork by the opponent. That would be easy to do:
|
1
2
3
|
(define (opponent-can-fork? triples me) ;; not really part of game
(i-can-fork? triples (opponent me)))
|
Unfortunately, although the programming works, the strategy doesn’t. Maybe the opponent has two potential forks;
🤔 What would two potential forks look like?
we can block only one of them. (Why isn’t that a concern when blocking the opponent’s wins? It is a concern, but if we’ve allowed the situation to reach the point where there are two ways the opponent can win on the next move, it’s too late to do anything about it.)
Instead, our strategy is to go on the offensive. If we can get two in a row on this move, then our opponent will be forced to block on the next move, instead of making a fork. However, we want to make sure that we don’t accidentally force the opponent into making a fork.
Ok, so there are two steps: get two in row, but make sure that doing so doesn’t force the opponent into making a fork. If you get two in a row, and then the opponent blocks you with a move that makes a fork, then that’s a kinda pyrrhic victory. The opponent will block you so you won’t win, and then you won’t be able to stop the opponent from winning. So you can’t just look at the game next moves from your point of view but need to look at them from the opponent’s point of view.
Let’s look at this board position again, but from
o‘s point of view:
The board position here is ‘xo__x___o
X‘s pivots are 4 and 7, as we discussed earlier;ocouldn’t take both those squares. Instead, look at the triples369and789, both of which are singles that belong too. Sooshould move in one of the squares 3, 6, 7, or 8, forcingxto block instead of setting up the fork. Butoshouldn’t move in square 8, like this:
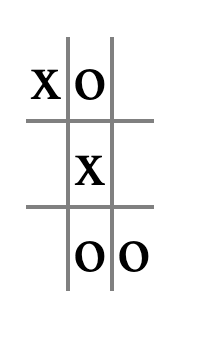
because that would force
xto block in square 7, setting up a fork!
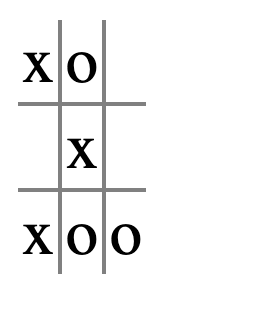
So o wants to make sure that a move doesn’t put x in an i-can-fork? position.
The structure of the algorithm is much like that of the other strategy possibilities. We use
keepto find the appropriate triples, take the first such triple if any, and then decide which of the two empty squares in that triple to move into.
|
1
2
3
|
(define (i-can-advance? triples me)
(best-move (keep (lambda (triple) (my-single? triple me)) triples) triples me))
|
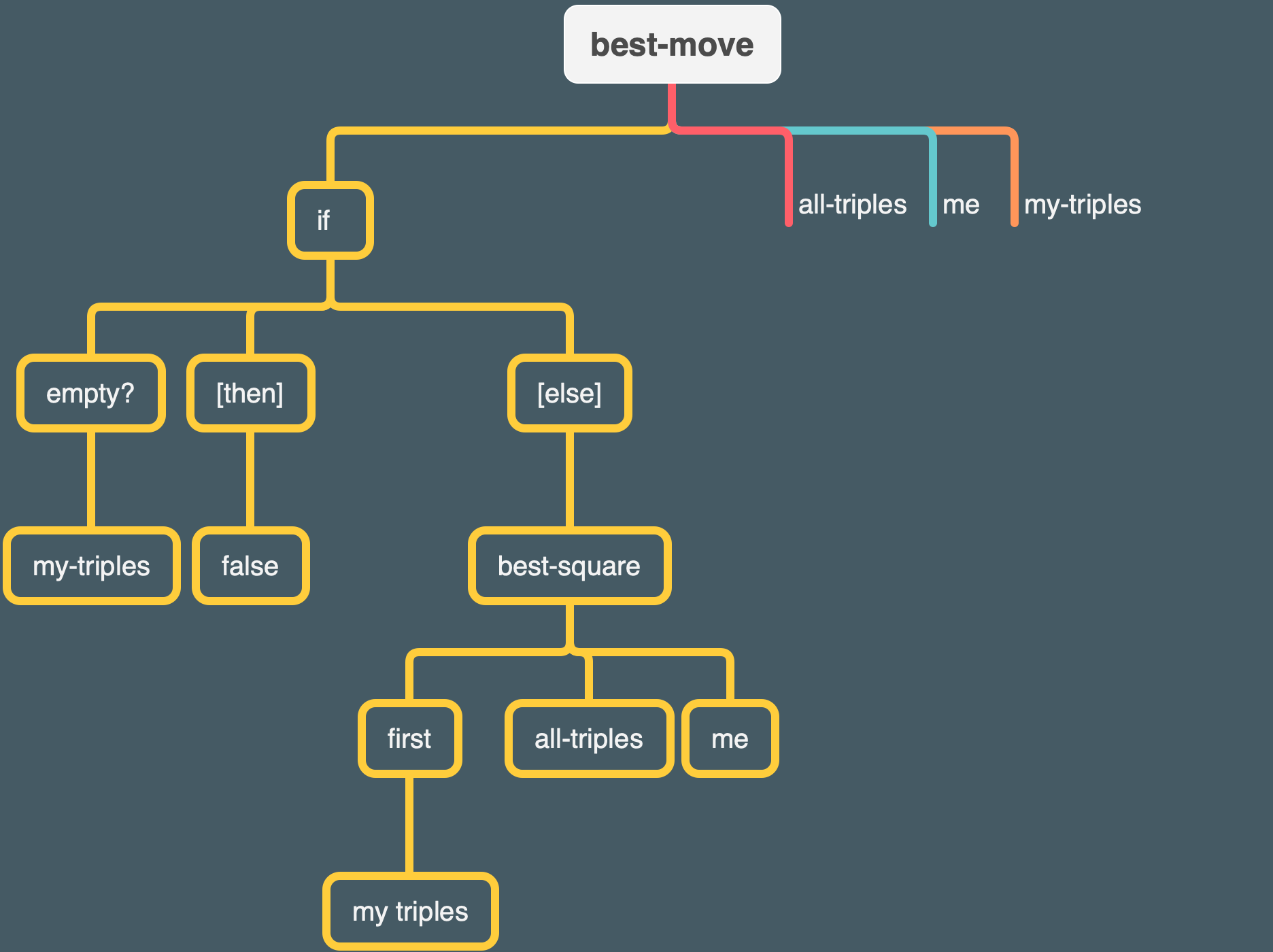
getting a little overwhelmed by all the procedures so I’m making trees to help me understand them.
For the board state 'xo__x___o mentioned above, for the following input:
|
1
2
|
(i-can-advance? (find-triples 'xo__x___o) 'o)
|
the value returned is 7 (note that I used find-triples so I could test this part of the procedure separately.)
|
1
2
3
4
|
(define (best-move my-triples all-triples me)
(if (empty? my-triples) #f
(best-square (first my-triples) all-triples me)))
|
Best-movedoes the same job asfirst-if-any, which we saw earlier, except that it also invokesbest-squareon the first triple if there is one.
Since we’ve already chosen the relevant triples before we get tobest-move, you may be wondering why it needs all the triples as an additional argument. The answer is thatbest-squareis going to look at the board position from the opponent’s point of view to look for forks.
Right okay. The triples that are relevant from our side’s perspective don’t address the issue of what potential moves the other player might make.
|
1
2
3
4
5
6
7
8
9
|
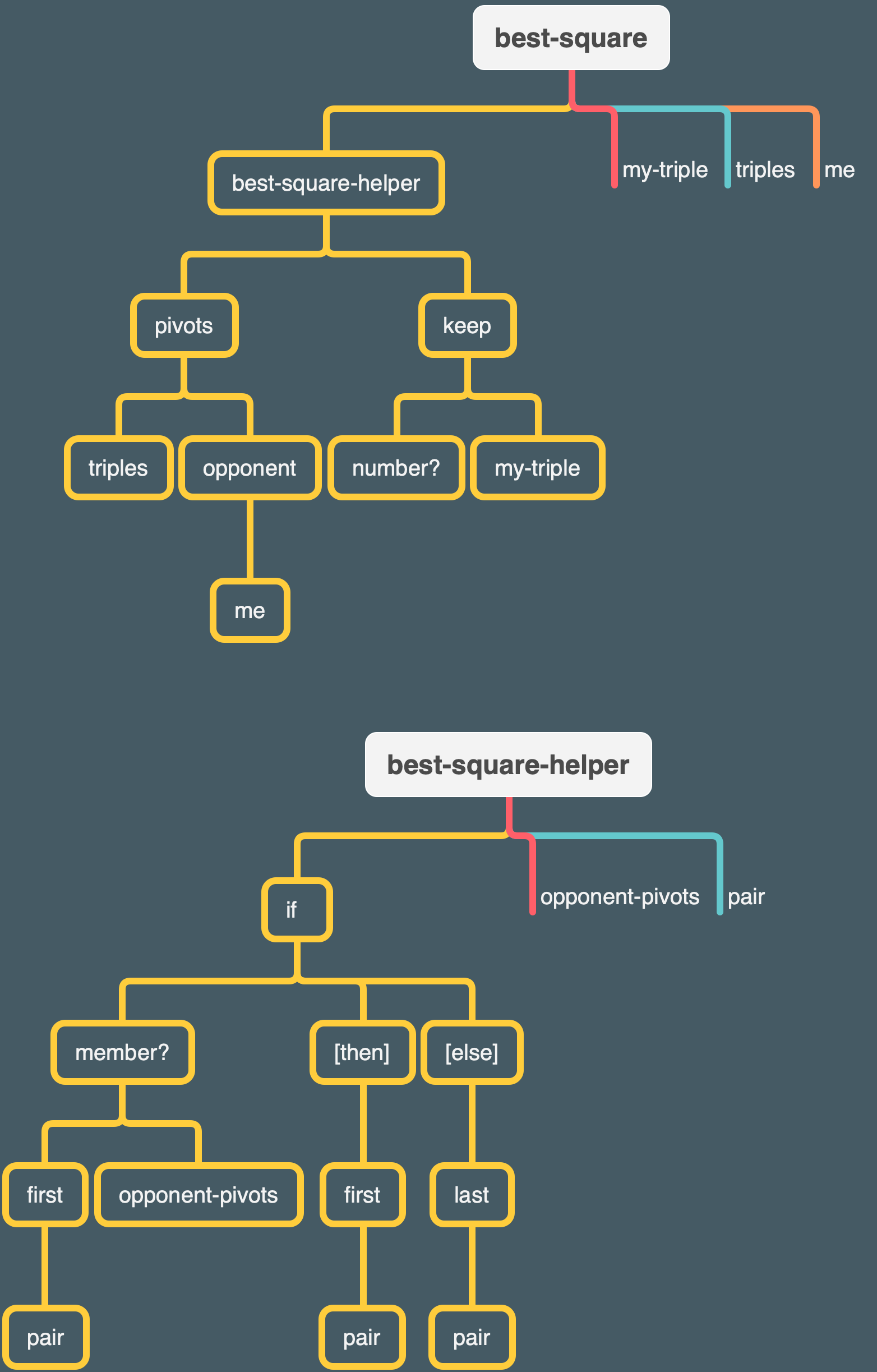
(define (best-square my-triple triples me)
(best-square-helper (pivots triples (opponent me)) (keep number? my-triple)))
(define (best-square-helper opponent-pivots pair)
(if (member? (first pair) opponent-pivots)
(first pair)
(last pair)))
|
We
keepthe two numbers of the triple that we’ve already selected. We also select the opponent’s possible pivots from among all the triples. If one of our two possible moves is a potential pivot for the opponent, that’s the one we should move into, to block the fork.
Right okay, and that’s what (if (member? (first pair) opponent-pivots) is doing – checking the two numbers of our triple against the opponent’s pivots.
Otherwise, we arbitrarily pick the second (
last) free square.
|
1
2
|
> (best-square "78o" (find-triples 'xo__x___o) 'o)7> (best-square "36o" (find-triples 'xo__x___o) 'o)6> (best-move '("78o" "36o") (find-triples 'xo__x___o) 'o)7> (i-can-advance? (find-triples 'xo__x___o) 'o)7
|
What if both of the candidate squares are pivots for the opponent? In that case, we’ve picked a bad triple; moving in either square will make us lose. As it turns out, this can occur only in a situation like the following:
If we chose the triple
3o7, then either move will force the opponent to set up a fork, so that we lose two moves later. Luckily, though, we can instead choose a triple like2o8. We can move in either of those squares and the game will end up a tie.
In principle, we should analyze a candidate triple to see if both free squares create forks for the opponent. But since we happen to know that this situation arises only on the diagonals, we can be lazier. We just list the diagonals last in the procedurefind-triples. Since we take the first available triple, this ensures that we won’t take a diagonal if there are any other choices.
Ah that’s clever.
Exercises
❌ Exercise 10.1
The
tttprocedure assumes that nobody has won the game yet. What happens if you invoketttwith a board position in which some player has already won? Try to figure it out by looking through the program before you run it.
So I think looking through the main cond in ttt-choose is a reasonable way to organize my answer to this:
|
1
2
3
4
5
6
7
|
(define (ttt-choose triples me)
(cond ((i-can-win? triples me))
((opponent-can-win? triples me))
((i-can-fork? triples me))
((i-can-advance? triples me))
(else (best-free-square triples)) ))
|
i-can-win?‘s helper procedure my-pair? looks for triples where the number of appearances of the computer’s marks is exactly 2. So I don’t think i-can-win would “catch” a winning board position.
i-can-fork?‘s helper procedure my-single? triples with 1 appearance of the opponent’s marks, so likewise it won’t “catch” the 3 case.
i-can-advance? also relies on my-single?, so the same logic applies.
So I think maybe ttt-choose would default to using best-free-square. I’m low-confidence on this though.
UPDATE: I tried playing with it some and it seemed to just recommend that I make moves without acknowledging that victory had occurred. By the way, I realized that depending on the game board, the program might actually find triples that meet the criteria of the strategy other than the “winning” triple. So basically my updated guess is that the program would analyze the game state as normal without taking into account the fact that there was a winner.
SECOND UPDATE: I missed the fact mentioned by AnneB that the program will return an error if there are no empty square
A complete tic-tac-toe program would need to stop when one of the two players wins. Write a predicate
already-won?that takes a board position and a letter (xoro) as its arguments and returns#tif that player has already won.
I used modifications of existing stuff in ttt and built on top of the existing program some. So note, this is intended to be run as an addition to the ttt program. It particular relies on find-triples, substitute-triple, and substitute-letter and can be run just with those parts.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
|
(define (already-won? position me)
(i-have-won (find-triples position) me))
(define (my-win? triple me)
(and (= (appearances me triple) 3)))
(define (i-have-won triples me)
(return-true-if-winner
(keep (lambda (triple) (my-win? triple me))
triples)))
(define (return-true-if-winner winning-triples)
(if (not (empty? winning-triples))
#t #f))
|
already-won? invokes i-have-won and generates the triples using find-triples.
i-have-won invokes choose-winner and uses my-win? to filter the triples for winning triples.
my-win? looks for triples where there are 3 appearances of the computer’s mark. There’s no checking for the opponent’s mark, because if there are actually 3 of the computer’s mark then you know the opponent’s mark number is 0.
return-true-if-winner returns #true if there are any winning triples (meaning triples where we’ve already won).
This program appears to work:
Ok so solves the problem but is wildly overcomplicated. Here’s buntine’s effort for comparison:
|
1
2
3
4
|
(define (already-won? position letter)
(member? (word letter letter letter)
(find-triples position)))
|
So this checks whether a word consisting of the letter three times is a member of the list of triples generated by (find-triples position). Very easy!
Here’s AnneB’s:
|
1
2
3
4
5
|
(define (already-won? position me)
(not (empty?
(keep (lambda (triple)
(equal? (word me me me) triple)) (find-triples position)))) )
|
I’m going to go through Anne’s procedure and then compare my procedure and Anne’s procedure.
Anne’s procedure works as follows:
The lambda checks whether a particular triple is equal to three instances of the computer’s mark me. This would indicate a winning triple. keep tests each triple generated by find-triples for whether it is true for (equal? (word me me me), and if the list of triples generated by keep is not empty? (indicating that there is at least one winning triple) then the whole procedure returns as true.
my my-win? procedure somewhat parallels the functionality of Anne’s (equal? (word me me me) in that the point is to check for three instances of the me letter.
My return-true-if-winner somewhat parallels the (not (empty? part of Anne’s procedure, although Anne returns the truth values directly using not rather than needing to use an if statement.
My i-have-won procedure parallels the part of Anne’s procedure starting at the keep. This seems like the part of my procedure that would be easiest to turn into something more elegant.
✅❌ Exercise 10.2
The program also doesn’t notice when the game has ended in a tie, that is, when all nine squares are already filled. What happens now if you ask it to move in this situation?
❌ (forgot to answer this part of the question at first): You get an error.

Write a procedure
tie-game?that returns#tin this case.
Here’s one solution (which makes use of the opponent procedure from ttt, although you could also just specify x and o)
|
1
2
3
4
|
(define (tie-game? position letter)
(equal? (+ (appearances letter position)(appearances (opponent letter) position))
9))
|
It checks if the number of appearances of the computer’s letter and the opponent’s letter total to 9.

Here’s another solution (from buntine), which doesn’t make use of letter:
|
1
2
3
|
(define (tie-game2? position)
(not (member? '_ position)))
|

AnneB’s solution, which actually incorporates an already-won? check, is better:
|
1
2
3
4
5
|
(define (tie-game? position)
(and (not (already-won? position ‘x))
(not (already-won? position ‘o))
(full-squares? position) ))
|
Exercise 10.3
A real human playing tic-tac-toe would look at a board like this:
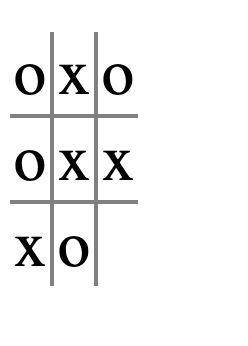
and notice that it’s a tie, rather than moving in square
9. Modifytie-game?from Exercise 10.2 to notice this situation and return#t.
Ok. A situation like the above always involves the following two things:
- There is exactly one space free
- The triples involving that space (in the above, 1-4-9, 3-6-9, and 7-8-9) have one x and one o respectively (so that neither side can actually win). If there was only one space free but one of the triples with that space had 2 appearances of the same letter, then that would mean we had a potentially winning move on our hands and not a tie.
So let’s think about this in terms of tie-game?. We want tie-game? to notice that there’s only one free space left. We also want it to notice that nobody can win by occupying that free space. So those are two separate requirements for tie-game?. The one free space one seems easiest, so we’ll start with that one:
|
1
2
3
|
(define (tie-game? position letter)
(equal? (appearances '_ position) 1))
|
One way to approach this problem is to create and compare filtered lists of triples. We can use one function, free-space-is-present?, to generate a list of all the triples in which the free space is present. We can use another function, triple-is-tie?, to generate a list of all the triples which fit the criteria for being a tie. If the board situation is truly one where a tie is inevitable, then the number of triples fitting both criteria should be identical. If one or another of the lists weren’t identical, that might indicate e.g. that there was a triple which included the free space and which did not fit the criteria for a tie (in other words, a potentially winning move).
We can say that a particular triple indicates a tie when all of the following conditions are met:
- We know there is only one free space left in the board
- A triple generated by
find-tripleshas a number value and not just x’s or o’s (this indicates that that particular triple has the free space), and - A triple generated by
find-tripleshas no more than one appearance of the computer’s mark (if it had 2, that would indicate a potentially winning move that the computer could make. If there’s only one free space left, then the opponent’s number of marks in a triple with the free space doesn’t matter)
A triple meeting 2 and 3 while 1 is true means that the free space in the triple can no longer be used to win by either side.
Since I want to ensure that 1 is true, I restructure (equal? (appearances '_ position) 1)) within an if. If (equal? (appearances '_ position) 1)), then the other stuff will be analyzed (and possibly return true or false). Otherwise the procedure will return false.
I also want to still cover the case where all there are no free spaces.
So I nest my more complex analysis as the alternative within an if statement that first checks whether 0 spaces are free:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
|
(define (tie-game? position letter)
(if (not (member? '_ position)) #t
(if (equal? (appearances '_ position) 1)
(equal?
(count
(keep
(lambda (triple)
(free-space-is-present? triple letter))
(find-triples position)))
(count
(keep
(lambda (triple)
(triple-is-tie? triple letter))
(find-triples position))))
#f)))
|
After doing the problems above, I refactored my program as follows and added testing for already-won?:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
|
; newer version
(define (already-won? position letter)
(member? (word letter letter letter)
(find-triples position)))
(define (tie-game? position letter)
(and (not (already-won? position letter))
(not (already-won? position (opponent letter)))
(equal?
(count
(keep
(lambda (triple)
(free-space-is-present? triple letter))
(find-triples position)))
(count
(keep
(lambda (triple)
(triple-is-tie? triple letter))
(find-triples position))))))
|
Here are some tests I ran:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
|
(tie-game? 'xoxoxoxo_ 'x)
;f - x won
;xox
;oxo
;xo_
(tie-game? 'xoxoxoo__ 'x)
;#f - x can win
;xox
;oxo
;o__
(tie-game? 'xoxxooox_ 'o)
;t - o can't win
;xox
;xoo
;ox_
(tie-game? 'oxoxoxxo_ 'o)
;f - o can win
;oxo
;xox
;xo_
(tie-game? 'oxoxoxoxo 'o)
;#f - o won
;oxo
;xox
;oxo
(tie-game? 'xoxoxoxo_ 'o)
;#f - opponent x won
;xox
;oxo
;xo_
|
For the first four tests, both versions produce the same result. For the final two tests, only the newer version produces the correct output. For the fifth test, I think that the new version of the procedure finds that the 1-5-9 triple has won and so (not (already-won? position letter)) correctly fails. For the sixth test, I think that the newer verison of the procedure correctly finds that the (not (already-won? position (opponent letter))) test fails due to x having won with triple 3-5-7.
(Can you improve the program’s ability to recognize ties even further? What about boards with two free squares?)
Let’s look at a scenario where there’s a tie. Assume the following board state, and o is going to move next:
‘xoxoox_x_ ‘o
xox
oox
_x_
o has no winning moves and can block x from winning by placing a square at 9. So this game has already deadlocked and should return true.
Here’s another case:
‘_oxxxoox_ ‘o
_ox
xxo
ox_
x can’t win if o moves in any of the remaining free spaces. o can’t win either.
One thing we haven’t done is figure out a way to update position based on a move, which I think would be essential for implementing this approach. So let’s try seeing if we can do that.
We want a procedure that can take a board position and player’s mark, figure out what move to make, and then update position.
So basically it would run ttt, take the value from that, and update the position based on the value. Whatever player’s mark was, it would replace that value in position.
Here’s my solution to this problem:
|
1
2
3
4
5
|
(define (position-updater position me)
(accumulate word (every (lambda (digit)
(if (equal? digit (ttt position me)) me (item digit position)))
'(1 2 3 4 5 6 7 8 9))))
|
I am borrowing heavily from the structure of the sort-digits procedure here. My procedure has a lambda which checks if a digit from a list of 1 through 9 is equal to the square returned by calling ttt on the current board state and with the player’s mark (x or o). If so, the player’s mark is returned. If not, a character representing the current board state (x, o, or _ indicating empty) is returned. every does this for 9 digits, representing 9 squares of the board, and returns a sentence. This sentence is then accumulated into a word in order to be in the original form of position.
I realized when I was working on this problem that my previous iteration of tie-game had an issue. For the two cases of facing a tie game two moves out that I mentioned above, 'xoxoox_x_ 'o and '_oxxxoox_ 'o respectively, my current tie-game? procedure returns #t. I want it to return #t ultimately after I make certain adjustments to handle the two-spaces-out case, but it shouldn’t be returning #t yet. So let’s see if we can fix that before we add further layers of complexity.
|
1
2
3
4
5
6
7
8
9
10
11
12
|
(define (tie-game? position letter)
(and (not (already-won? position letter))
(not (already-won? position (opponent letter)))
(and (equal? (appearances '_ position) 1)
(equal?
(count (keep (lambda (triple)
(free-space-is-present? triple letter))
(find-triples position)))
(count (keep (lambda (triple)
(triple-is-tie? triple letter))
(find-triples position)))))))
|
I’ve added (and (equal? (appearances '_ position) 1) and that flips my two new test cases to false, as desired.
I’m also wondering if there is some way to simplify the program here along the lines I figured out already when trying to have the program handle two free spaces.
Oh. So if there is one free space, and the player can’t win, and the opponent has not already won, then that’s a tie. We’re already always checking for whether the opponent has already won, because we want to know whether either player has won regardless of whether there’s 4 free moves left or 0. So I think in the case where there is one free space left, we just need to check for whether the player will have already won after making the best move!
|
1
2
3
4
5
6
|
(define (tie-game? position letter)
(and (not (already-won? position letter))
(not (already-won? position (opponent letter)))
(and (equal? (appearances '_ position) 1)
(not (already-won? (position-updater position letter) letter)))))
|
Ok, now we’ve got the 0 and 1 free space cases handled more elegantly!
Now to go to two spaces. Wait, first, I think since we’re handling more cases, we might want to go to a cond expression. Let me translate what I have into that first.
Let’s think about this. So if someone’s already won, that’s always going to be a not-tie situation, so that can go first, and we want to return false for tie-game? in that case.
|
1
2
3
4
|
(define (tie-game? position me)
(cond (or ((already-won? position me)
(already-won? position (opponent me))) #f)...
|
Next, I think we want to test the two free spaces case. My intuition is that if the program can see that the game is a tie two spaces out, we don’t need to worry about testing the one free space case. The one free space case is like a subset of the two free spaces case. So we can just stop there and return false.
So one way to think of the two free spaces case is in terms of the following questions:
1. Can the player win?
2. Supposing that the player makes the best move regardless of whether they can win or not, can the opponent win?
So what you’d want to do to check for a tie-game two spaces out is to first see if the player can win, which is something we can already ask using our existing tools. Then look at the game from the opponent’s perspective but with the assumption that the player has made the best possible move in their next move, and then ask if the opponent can win. If the player can win, or the opponent can win, then the game is not tied, and this part of the procedure should return #f.
|
1
2
3
4
5
6
7
|
(define (tie-game? position me)
(cond ((or (already-won? position me)
(already-won? position (opponent me))) #f)
((and (equal? (appearances '_ position) 2)
(or (i-can-win? (find-triples position) me)
(opponent-can-win? (find-triples (position-updater position me)) me))) #f)...
|
A thought occurs to me. Since we have something that can “look ahead” and judge ties with two free spaces, do we need to address 1 free space case specifically?
Another way of asking this question: are ties with one free space left a perfect subset of ties with two free spaces left?
I think one free space ties are not a perfect subset of two-space ties, and so we do need to test the 1 free space case separately. Why? Because one of the assumptions we make for the player’s move when testing whether there is a tie two free spaces out is that they make the best possible move. However, it is possible that the player fails to make the best possible move, and that that creates a tie-game situation due to the error of the player. So I think we want to test for that possibility.
I also realized a better way to test for this case. Just ask: is it true that the number of free spaces is equal to 1 and that player can win? If so, that’s not a tie-game, so return false. Since we’ve already asked if opponent has already won, we just need to know whether player 1 can win.
|
1
2
3
4
5
6
7
8
9
|
(define (tie-game? position me)
(cond ((or (already-won? position me)
(already-won? position (opponent me))) #f)
((and (equal? (appearances '_ position) 2)
(or (i-can-win? (find-triples position) me)
(opponent-can-win? (find-triples (position-updater position me)) me))) #f)
((and (equal? (appearances '_ position) 1) (i-can-win? (find-triples position) me)) #f)
(else #t)))
|
After glancing at buntine’s answer, I added a let statement to clean things up a bit:
|
1
2
3
4
5
6
7
8
9
10
11
|
(define (tie-game? position me)
(let ((underscores (appearances '_ position)))
(cond ((or (already-won? position me)
(already-won? position (opponent me))) #f)
((and (= underscores 2)
(or (i-can-win? (find-triples position) me)
(opponent-can-win? (find-triples (position-updater position me)) me))) #f)
((and (= underscores 1) (i-can-win? (find-triples position) me)) #f)
(else #t))))
|
I also noticed that neither buntine nor AnneB specified which player was making the next move for their versions of tie-game. I’m not quite sure if I made a mistake in doing so/if that was unnecessary to do on my part.
In the way I’ve currently structured the program, except for the check for whether either side has already won, the information about who the next player to move is going to be seemed necessary. But then I read Anne’s solution a bit and realized that if there’s two spaces left and only two possible moves in each space, that’s only two possibilities to check.
Here’s a modification dropping the use of me for the already-won? case:
|
1
2
3
4
5
6
7
8
9
10
11
|
(define (tie-game? position me)
(let ((underscores (appearances '_ position)))
(cond
((or (already-won? position 'x)
(already-won? position 'o)) #f)
((and (= underscores 2)
(or (i-can-win? (find-triples position) me)
(opponent-can-win? (find-triples (position-updater position me)) me))) #f)
((and (= underscores 1) (i-can-win? (find-triples position) me)) #f)
(else #t))))
|
Exercise 10.4
Here are some possible changes to the rules of tic-tac-toe:
What if you could win a game by having three squares forming an L shape in a corner, such as squares 1, 2, and 4?
Answer the following questions for each of these modifications separately:
What would happen if we tried to implement the change merely by changing the quoted sentence of potential winning combinations infind-triples?
Would the program successfully follow the rules as modified?
I ran some tests and it appears to. I made the following modification find-triples:
|
1
2
3
4
|
(define (find-triples position)
(every (lambda (comb) (substitute-triple comb position))
'(123 456 789 147 258 369 159 357 124 236 478 698)))
|
and ran the following tests:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
|
(ttt 'ox_xoxoxo 'x)
3
;ox_
;xox
;oxo
(ttt 'xoo___x_x 'o)
;6
;xoo
;___
;x_x
(ttt 'x_o__ox_x 'o)
2
;(and not 8 to block, since 2 is a winning move)
;x_o
;__o
;x_x
|
(the comments in semi-colons represent a graphical depiction of the tic-tac-toe board state, since it’s easier for me to understand the board state that way).
I guess based on the program design this makes sense. find-triples is generated earlier on and then those triples are fed by ttt into the strategy procedure ttt-choose. So the triples list “flows down” into every portion of the program. So because the triples list is the reference point for whether a pair is winning, changing it can allow the program to adapt to different rules, at least if the rule change still involves a triple. The idea of trying to get a particular set of three values in order to win is hardcoded into the math of procedures like my-pair?. So this particular change works, but if you wanted to move to a system where you need like, an L shape to win (like 1-2-3-4, for example) then I don’t think the existing program would be able to handle that. You’d need to make more changes to handle that case.
Going into more detail: suppose you have something like the following board state:
|
1
2
3
4
5
|
(ttt 'xoo___x_x 'o)
;xoo
;___
;x_x
|
Under the normal rules of tic-tac-toe, if you were o and making the next move here, you’d want to occupy square 8 in order to block x from winning and also to build a potential 2-5-8 triple. And indeed, the normal tic-tac-toe program returns 8 for this.
But with a “corners win” modification, you want to return 6 in order to win. And with the modification above, the procedure my-pair? will see that 2-3-6 is a potentially winning triple, and then return 6 according, which it does.
What if the diagonals didn’t win?
What would happen if we tried to implement the change merely by changing the quoted sentence of potential winning combinations in
find-triples?
Would the program successfully follow the rules as modified?
I think this change would work based on the reasoning above.
The change would be reflected in the following code, which has removed the diagonal triples:
|
1
2
3
4
|
(define (find-triples position)
(every (lambda (comb) (substitute-triple comb position))
'(123 456 789 147 258 369)))
|
So for the following board state:
|
1
2
3
4
5
|
(ttt 'xo__xo___ 'x)
;xo_
;_xo
;___
|
I would expect the unaltered ttt program to return a 9 (in order to win) and the modified program to return a 4 or an 7 (to try to build a 1-4-7 triple)
Both programs performed as expected.
What if you could win by having four squares in a corner, such as 1, 2, 4, and 5?
What would happen if we tried to implement the change merely by changing the quoted sentence of potential winning combinations in
find-triples?
Would the program successfully follow the rules as modified?
I would expect this change to fail if implemented by editing find-triples, for the reason stated above. To recap, the idea of trying to get a particular set of three values in order to win is hardcoded into the math of procedures like my-pair?. So if you wanted to move to a system where you need like, an L shape to win (like 1-2-3-4, for example) then I don’t think the existing program would be able to handle that just by modifying find-triples. You’d need to make more substantial changes.
I changed the code as follows to test this:
|
1
2
3
4
|
(define (find-triples position)
(every (lambda (comb) (substitute-triple comb position))
'(123 456 789 147 258 369 159 357 1245 2356 4578 5689)))
|
Now consider the following board state:
|
1
2
3
4
5
|
(ttt 'xxox_oo__ 'x)
xxo
x_o
o__
|
I’d expect the standard ttt program to attempt to block the computer from winning at 9. I’d expect the modified procedure to do the same.
My prediction was correct.
Exercise 10.5
Modify ttt to play chess.
Sounds hard, especially since I don’t know anything about chess. I’m going to skip this one for now.
Trees
After reviewing her work on this chapter, I tried making some trees like AnneB did, to see the overall structure of the whole program.
Initially I thought the more detailed tree AnneB made looked overwhelming, but then I realized that I’d already some of the work in terms of describing what each part of the program did. Filling in the gaps and elaborating was a significant amount of additional work though.
Making the more detailed tree had a concrete benefit for me: I did not actually understand in detail the operation of opponent-can-win? or the various subprocedures within pivots or i-can-advance? previously. I had a sort of vague idea but making the tree gave me a more solid appreciation. I mention this as a reminder to myself of the value of making the tree, since I seem to still be somewhat skeptical and do such things in an inconsistent manner.
Things to Improve
Some of it is stuff I’ve mentioned before:
- Use trees more (like, I could have made a tree of the whole program).
- Do more thorough testing.
- Integrate past solutions into future steps (like Anne did with integrating already-won? into tie-game).
- (specific to this chapter) A failure to represent the tic-tac-toe board pictorially caused me some confusion about the board game state when coming up with tests. I fixed this as I went along.
Not sure if I’m overreaching or just failing to consistently apply best practices or something, but I found this chapter pretty difficult to work through. Possibly my standards are still not high enough in some way. I think part of the difficulty may have been that I’d worked through a lot of the material for the previous chapters in the past, but I might have skipped over most of this chapter previously, so it was kind of like totally new material. Since the next chapter looks to be stuff I’ve worked through before, I think I should go through it with some sort of checklist in order to use those (hopefully relatively easier problems) as an opportunity to work on developing some skills. Here are some things I’m thinking of having on my checklist:
- Make trees of procedures.
- Describe what each part of a procedure does in detail. Domain, range, big picture role, detailed steps.
- Figure out tests, including tests that try to go at least a bit beyond the scope of what the text says and make sense in terms of input someone might give an actual program (like – can the program handle erroneous input?)
- Ensure that I represent important information to myself in a way that’s easy for me to check for errors and issues (this came up with my initial failure in Chapter 10 to represent my tic-tac-toe test cases pictorially, which wasted some time)
- Integrate past solutions to problems into future steps in order to make procedures I write more robust/able to handle more cases (instead of treating each procedure as its own thing).
- Consider whether parameter names are reasonable.
- Consider whether there is redundant or unnecessary functionality. Consider especially whether
ifstatements are needed. - Carefully check each line of a program for parentheses issues when I’m done writing.
- Don’t rush to artificial deadlines. Focus on mastery not speed.