This post is fairly short, as much of my attention for chapter 9 was spent on trying to just understand the Y-Combinator material in Chapter 9. My YouTube video has lots of content on this point.
Some stuff I looked at while making my video and writing this post:
https://catonmat.net/derivation-of-ycombinator
https://mvanier.livejournal.com/2897.html
https://github.com/ggandor/y-combinator-tutorial
https://www.youtube.com/watch?v=9T8A89jgeTI
https://www.macadie.net/2020/02/02/chapter-9-of-the-little-schemer/
https://wyounas.medium.com/deriving-y-combinator-in-scheme-dd68a02973f9
Selected Portions of Dialogues
I decided to refer to these as dialogues since the book doesn’t really have exercises per se.
looking & keep-looking

My tentative initial guess about how all this works is that the procedures involved use the numbers that appear as the elements of the list to figure out which elements of the lat to check as being possible matches for a.
Ok I think I figured it out. looking first checks the initial element of the list. If that element is a match for a. looking returns true. If it’s a word that’s not a match for a, looking returns false. If it’s a number, looking uses that number and then checks the element of the list that corresponds to that number (starting from 1), and then runs the same checks.
At this point, I tried writing keep-looking:
|
1
2
3
4
5
6
7
8
9
10
11
12
|
(define looking
(lambda (a lat)
(keep-looking a (pick 1 lat) lat)))
(define keep-looking
(lambda (a sel lat)
(cond
((equal? a sel) #t)
((number? sel)
(keep-looking a (pick sel lat) lat))
(else #f))))
|
It seems to work 🙂
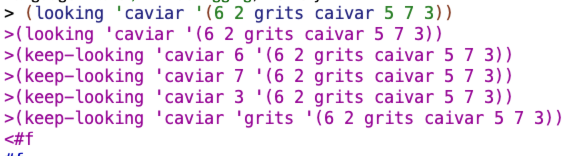

After looking at their version, I realized mine was overly complicated:

Their structure is basically: if you know it’s a number, continue on with a recursive call, but if you know it’s not, just check whether a is equal to sorn (their sel). That else is gonna be true or false, so it covers both cases.
Shift



A pair is a list with only two s-expressions.
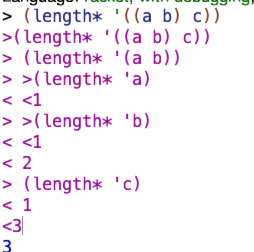
length*
needed the book’s help on this one

Why does it work? Seems worth analyzing a brief example since I couldn’t write the procedure on my own.
for a pora of ‘((a b) c)), the atom? test fails, so the procedure recursively calls length\* twice – once on (a b) and once on c. c is an atom so that branch returns 1. (a b) isn’t an atom and so it recursively gets passed to length*again as a and b respectively. These are atoms and so they get added up to 2, and then that 2 is added to the 1 from c and we get 3.
weight*
I did not really understand the rationale for the weight* procedure. I did analyze it though. They want to “weigh” the first part of the argument given to align more heavily for some reason, and not just count the number of atoms.

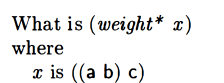
This is 7 because
- the a gets 2X as the first element of (a b)
- The (a b) gets 2X as the first element of the whole x
and then it’s just arithmetic
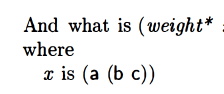
shuffle

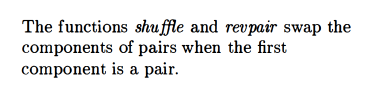
![]()
The function is partial. For the input ((a b)(c d)), it will loop endlessly, because it will keep reversing the order of the pairs and invoking shuffle on them.
will-stop?

They wind up guiding you towards logically proving that will-stop? can’t be defined for logical reasons. See the video above for details, as I found this part difficult to summarize.