Lambda
lambda lets us generate procedures without having to give them a name. This can lead to nicer program organization compared with the alternatives (such as making a helper function):
|
1
2
3
4
5
6
|
define (add-three-to-each sent)
(every (lambda (number) (+ number 3)) sent))
> (add-three-to-each '(1 9 9 2))
(4 12 12 5)
|
Another example, which uses lambda to provide a procedure to the higher order function accumulate:
|
1
2
3
4
5
6
|
> (accumulate (lambda (this that)
(if (> (count this) (count that)) this that))
'(wild honey pie))
HONEY
|
I think this is going through the words of 'wild honey pie one by one. If the first word is greater than the second word, it returns the first word. Otherwise, it returns the second word. Since it’s only returning one value each time and not actually combining anything, you only wind up with one word in the end.
Define & Let
define actually gives a name to values. lambda creates procedures. (define (square x) (* x x)) is short for (define square (lambda (x) (* x x))).
In this example, the job of
lambdais to create a procedure that multiplies its argument by itself; the job ofdefineis to name that proceduresquare.
In something like (* x x), the * has to be substituted just like the x does. But for * there’s a global definition that’s been predefined by define.
Just as the notation to define a procedure with parentheses around its name is an abbreviation for a
defineand alambda, theletnotation is an abbreviation for alambdaand an invocation.
When to Name Functions
Use names for procedures when you can give a meaningful name that will help clarify the program.
Use names for stuff that you’ll use often.
Shorter Notes
Don’t use the same formal parameter for both a procedure and a procedure inside a procedure.
Boring Exercises
✅❌ Exercise 9.1
What will Scheme print? Figure it out yourself before you try it on the computer.
|
1
2
|
> (lambda (x) (+ (* x 3) 4))
|
I predicted that this would return a procedure which takes a value, multiplies it by 3, and adds 4.
❌ I was correct in my description but a bit non-responsive to the question. I should have said “it will print something indicating that scheme is returning a procedure”.
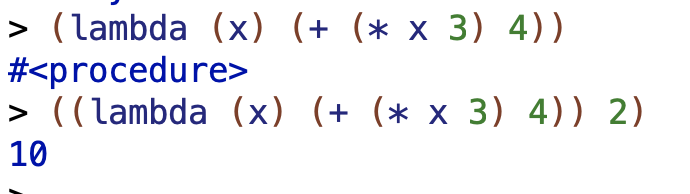
|
1
2
|
((lambda (x) (+ (* x 3) 4)) 10)
|
✅ I correctly predicted that this would print 34.
|
1
2
3
4
|
(every (lambda (wd) (word (last wd) (bl wd)))
'(any time at all))
|
✅ I correctly predicted that this would print'(yan etim ta lal). The lambda will create a word that starts with the last character of each word and then combines that with all but the last characters of each word, and then every will return a sentence full of such words (one for each word in the sentence).
|
1
2
|
((lambda (x) (+ x 3)) 10 15)
|
This seems to have too many arguments for the lambda. I predict an error message about too many arguments.
✅ Yup.

✅ Exercise 9.2
Rewrite the following definitions so as to make the implicit lambda explicit.
|
1
2
3
|
(define (second stuff)
(first (bf stuff)))
|
rewrite:
|
1
2
3
|
(define second (lambda (stuff)
(first (bf stuff))))
|
|
1
2
3
|
(define (make-adder num)
(lambda (x) (+ num x)))
|
Rewrite:
|
1
2
3
|
(define make-adder (lambda (num)
(lambda (x) (+ num x))))
|
✅ Exercise 9.3
What does this procedure do?
|
1
2
3
|
(define (let-it-be sent)
(accumulate (lambda (x y) y) sent))
|
The lambda defines two formal parameters, x and y. The lambda always returns y. accumulate typically operates by applying a procedure to two variables that combines them in some way. There is no combining going on here, however. So the ultimate result, I think, will be that what gets returned is the last word of a sentence.
✅ Yup. It also returns the last letter of a word.
Real Exercises
✅ Exercise 9.4
The following program doesn’t work. Why not? Fix it.
|
1
2
3
4
5
6
|
(define (who sent)
(every describe '(pete roger john keith)))
(define (describe person)
(se person sent))
|
It’s supposed to work like this:
|
1
2
3
|
> (who '(sells out))
(pete sells out roger sells out john sells out keith sells out)
|
What we want in the spot where describe is is something that returns a procedure that can take the input sent and apply it to the '(pete roger john keith)) sentence.
The describe program seems to assume it can take sent as an argument, but sent is never provided to describe.
We can make this work with lambda
|
1
2
3
|
(define (who sent)
(every (lambda (person) (se person sent)) '(pete roger john keith)))
|
In each of the following exercises, write the procedure in terms of lambda and higher-order functions. Do not use named helper procedures. If you’ve read Part IV, don’t use recursion, either.
✅ Exercise 9.5
Write prepend-every:
|
1
2
3
4
5
6
|
> (prepend-every 's '(he aid he aid))
(SHE SAID SHE SAID)
> (prepend-every 'anti '(dote pasto gone body))
(ANTIDOTE ANTIPASTO ANTIGONE ANTIBODY)
|
Answer:
|
1
2
3
4
|
(define (prepend-every prefix sent)
(every (lambda (wd) (word prefix wd)) sent))
|
✅ Exercise 9.6 – Note about lambda and program structure
Write a procedure
sentence-versionthat takes a function f as its argument and returns a function g. f should take a single word as argument. g should take a sentence as argument and return the sentence formed by applying f to each word of that argument.
|
1
2
3
4
5
6
|
> ((sentence-version first) '(if i fell))
(I I F)
> ((sentence-version square) '(8 2 4 6))
(64 4 16 36)
|
Answer:
|
1
2
3
4
|
(define (sentence-version func)
(lambda (sent)
(every (lambda (wd) (func wd)) sent)))
|
NOTE: My answer works but is unnecessarily complicated. I recreated some of the functionality of every unnecessarily. every can already apply a function to each word of a sentence. AnneB’s version is more elegant:
|
1
2
3
|
(define (sentence-version f)
(lambda (sent) (every f sent)) )
|
This problem illustrates an important distinction in the text:
For example, here is a procedure to keep the words of a sentence that contain the letter
h. The domain of the function is sentences, and its range is also sentences. (That is, it takes a sentence as argument and returns a sentence as its value.)
|
1
2
3
|
(define (keep-h sent)
(keep (lambda (wd) (member? 'h wd)) sent))
|
By contrast, here is a function of a letter that returns a procedure to keep words containing that letter.
|
1
2
3
|
(define (keeper letter)
(lambda (sent)(keep (lambda (wd) (member? letter wd)) sent)))
|
The procedure
keeperhas letters as its domain and procedures as its range. The procedure returned bykeeperhas sentences as its domain and as its range, just askeep-hdoes.
In keep-h, the lambda returns a procedure which looks to see if h is part of a word, but that procedure is returned to the keep and is used directly on the input to keep-h. The lambda isn’t the highest level thing in the procedure, so the procedure it returns is used by the higher-order function keep.
OTOH with keeper, the lambda is the highest level thing in the keeper. It’d be the root of a tree of the function. So the lambda has nothing within the program to return a procedure to. Therefore, the overall procedure returns a procedure.
✅ Exercise 9.7
Write a procedure called
letterwordsthat takes as its arguments a letter and a sentence. It returns a sentence containing only those words from the argument sentence that contain the argument letter:
|
1
2
|
> (letterwords 'o '(got to get you into my life))(GOT TO YOU INTO)
|
Answer:
|
1
2
3
|
(define (letterwords letter sent)
(keep (lambda (wd) (if (member? letter wd) #t #f)) sent))
|
The lambda returns a predicate procedure which checks if the value for letter is present in a word. If this is so, the lambda procedure returns true; otherwise, it returns false. keep applies the procedure returned by lambda to each of the words in the sent, and keeps the ones for which the value of the lambda procedure is true.
NOTE: again, my program is a bit inelegant. The if is unnecessary. keep can work just fine with a lambda procedure that checks if letter is a member of a word in a more straightforward way. AnneB’s version:
|
1
2
3
4
5
6
|
> (define (letterwords letter sent)
(keep (lambda (w) (member? letter w)) sent) )
> (letterwords ‘o ‘(got to get you into my life))
(got to you into)
|
Since the (member? letter w) returns true or false, it’s an appropriate predicate for keep without needing to toss an if statement in there.
✅🤔 Exercise 9.8
Suppose we’re writing a program to play hangman. In this game one player has to guess a secret word chosen by the other player, one letter at a time. You’re going to write just one small part of this program: a procedure that takes as arguments the secret word and the letters guessed so far, returning the word in which the guessing progress is displayed by including all the guessed letters along with underscores for the not-yet-guessed ones:
|
1
2
|
> (hang 'potsticker 'etaoi)_OT_TI__E_
|
Hint: You’ll find it helpful to use the following procedure that determines how to display a single letter:
|
1
2
3
|
(define (hang-letter letter guesses)
(if (member? letter guesses) letter '_))
|
This question is ambiguous. I initially thought they wanted us to use the hang-letter procedure directly. I based this on the statement:
You’ll find it helpful to use the following procedure that determines how to display a single letter:
They said use, not “look at” or “draw inspiration from” or something like that.
OTOH, after exercise 9.4 there is the following instruction:
In each of the following exercises, write the procedure in terms of lambda and higher-order functions. Do not use named helper procedures. If you’ve read Part IV, don’t use recursion, either.
I read this as applying to all the remaining exercises, since it says “each”. I read 9.8 as being an exception to that instruction (it’s like how in law, a more specific rule in a subset of X tends to control versus a more general rule at a higher level of X, unless there’s something that says “this rule trumps other stuff”.)
So anyways I read what we were supposed to do one way. buntine appears to agree with my reading. So I solved it my way, but then started to read AnneB’s answer in which she took the helper procedure as more of a hint for making a procedure with no helper procedures. At that point I stopped reading AnneB’s answer to try to figure something similar to her approach by myself.
An issue with my initial solution (before reading AnneB’s stuff) is that I didn’t return the correct thing …. I wanted a word and not a sentence.
Initial Answer:
|
1
2
3
4
|
(define (hang wd guesses)
(every (lambda (letter) (hang-letter letter guesses)) wd))
|
Corrected initial answer:
|
1
2
3
|
(define (hang wd guesses)
(accumulate word (every (lambda (letter) (hang-letter letter guesses)) wd)))
|
Description: the lambda procedure returns a letter if the letter matches a word containing the existing guesses, and returns an underscore if the letter does not match the guesses. every applies the lambda procedure to each letter of a word and returns the results as a sentence.
Okay so let’s try rewriting the procedure without a separate hang-letter.
|
1
2
3
4
5
|
(define (hang wd guesses)
(accumulate word (every (lambda (letter) (if (member? letter guesses)
letter
'_)) wd)))
|
This version has a lambda that checks if a letter is a member of the list of existing guesses. If so, it returns that letter. Otherwise, it returns an underscore. every applies this lambda procedure to each letter in the list of existing guesses and returns a sentence. accumulate word takes this sentence and transforms it into a word.
I checked and my second version is basically the same as AnneB’s aside from the fact that mine returns a word.
✅ Exercise 9.9
Write a procedure
common-wordsthat takes two sentences as arguments and returns a sentence containing only those words that appear both in the first sentence and in the second sentence.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
|
(define (common-words sent1 sent2)
(keep (lambda (sent1-wd) (member? sent1-wd sent2)) sent1))
(common-words '(potato ninja hatface) '(tomato hockeypuck ninja))
;'(ninja)
(common-words '(kirby pokemon soccer wrestling laserswords)
'(knights dalinar potato kirby wrestling fencing))
;'(kirby wrestling)
|
The lambda checks a word in sent1 and sees if it’s a member of sent2. keep applies this lambda procedure to each word in sent1, so that each word in sent1 is checked for its membership in sent2, and words that return true as members are kept and returned by common-words.
✅ Exercise 9.10
In Chapter 2 we used a function called
appearancesthat returns the number of times its first argument appears as a member of its second argument. Implementappearances.
Answer:
|
1
2
3
|
(define (appearances2 arg1 arg2)
(accumulate + (every (lambda (arg2-element) (if (equal? arg1 arg2-element) 1 0)) arg2)))
|
I checked to make sure that the values returned were the same as the version of appearances I’d played around with earlier:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
|
(appearances2 7 'potato7potato7potato7)
; 3
(appearances2 34 'potato34potato34potato34potato3)
;0
(appearances2 9 89989)
; 3
(appearances2 'p 'pppp)
;4
(appearances2 'd '(d d))
;2
(appearances2 'd '(dd d))
; 1
|
AnneB’s version is more elegant since she used count and keep whereas I used accumulate and returning number values:
|
1
2
3
|
(define (appearances2 item longer-thing)
(count (keep (lambda (member) (equal? member item)) longer-thing)))
|
✅ Exercise 9.11
Write a procedure
unabbrevthat takes two sentences as arguments. It should return a sentence that’s the same as the first sentence, except that any numbers in the original sentence should be replaced with words from the second sentence. A number2in the first sentence should be replaced with the second word of the second sentence, a6with the sixth word, and so on.
|
1
2
3
4
5
6
7
8
|
> (unabbrev '(john 1 wayne fred 4) '(bill hank kermit joey))
(JOHN BILL WAYNE FRED JOEY)
> (unabbrev '(i 3 4 tell 2) '(do you want to know a secret?))
(I WANT TO TELL YOU)
|
Answer:
|
1
2
3
|
(define (unabbrev sent1 sent2)
(every (lambda (sent1-wd) (if (number? sent1-wd) (item sent1-wd sent2) sent1-wd)) sent1))
|
Here is AnneB’s for comparison:
|
1
2
3
4
5
6
7
8
|
(define (unabbrev sentence1 sentence2)
(every
(lambda (word1)
(if (number? word1)
(first ((repeated butfirst (- word1 1)) sentence2))
word1))
sentence1))
|
I think this time my solution is more elegant, cuz I think using item to pull the appropriate word is more elegant than doing the (first ((repeated butfirst (- word1 1)) sentence2)) thing.
✅ Exercise 9.12
Write a procedure
first-lastwhose argument will be a sentence. It should return a sentence containing only those words in the argument sentence whose first and last letters are the same:
|
1
2
3
|
> (first-last '(california ohio nebraska alabama alaska massachusetts))
(OHIO ALABAMA ALASKA)
|
answer:
|
1
2
3
|
(define (first-last sent)
(keep (lambda (wd) (if (equal? (first wd)(last wd)) #t #f)) sent))
|
another example of inelegance. you can just return the truth value provided by equal? to keep directly, like AnneB does:
|
1
2
3
|
> (define (first-last sentence-list)
(keep (lambda (wd) (equal? (first wd) (last wd))) sentence-list))
|
✅ Exercise 9.13
Write a procedure
composethat takes two functions f and g as arguments. It should return a new function, the composition of its input functions, which computes f(g(x)) when passed the argument x.
|
1
2
3
4
5
6
7
8
|
> ((compose sqrt abs) -25)
5
> (define second (compose first bf))
> (second '(higher order function))
ORDER
|
Answer:
|
1
2
3
|
(define (compose f g)
(lambda (arg) (f (g arg))))
|
✅ Exercise 9.14
Write a procedure
substitutethat takes three arguments, two words and a sentence. It should return a version of the sentence, but with every instance of the second word replaced with the first word:
|
1
2
|
> (substitute 'maybe 'yeah '(she loves you yeah yeah yeah))(SHE LOVES YOU MAYBE MAYBE MAYBE)
|
My initial answer:
|
1
2
3
|
(define (substitute wd1 wd2 sent)
(every (lambda (sent-wd) (if (equal? sent-wd wd2) wd1 sent-wd)) sent))
|
the lambda checks if a word in the sentence sent-wd is equal to the second word wd2. If so, it returns wd1, which effectively replaces wd2 with wd1. Otherwise, it returns sent-wd, which leaves the word from the sentence in place. every applies this to each word of sent and returns a sentence with the result.
✅ Exercise 9.15
Many functions are applicable only to arguments in a certain domain and result in error messages if given arguments outside that domain. For example,
sqrtmay require a nonnegative argument in a version of Scheme that doesn’t include complex numbers. (In any version of Scheme,sqrtwill complain if its argument isn’t a number at all!) Once a program gets an error message, it’s impossible for that program to continue the computation.
Write a proceduretype-checkthat takes as arguments a one-argument procedurefand a one-argument predicate procedurepred.Type-checkshould return a one-argument procedure that first appliespredto its argument; if that result is true, the procedure should return the value computed by applyingfto the argument; ifpredreturns false, the new procedure should also return#f:
answer:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
|
(define (type-check f pred)
(lambda (arg) (if (pred arg) (f arg) #f)))
(define safe-sqrt (type-check sqrt number?))
(safe-sqrt 16)
;4
(safe-sqrt 'sarsaparilla)
;#F
|
✅ Exercise 9.16
In the language APL, most arithmetic functions can be applied either to a number, with the usual result, or to a vector-the APL name for a sentence of numbers-in which case the result is a new vector in which each element is the result of applying the function to the corresponding element of the argument. For example, the function
sqrtapplied to16returns4as in Scheme, butsqrtcan also be applied to a sentence such as(16 49)and it returns(4 7).
Write a procedureaplizethat takes as its argument a one-argument procedure whose domain is numbers or words. It should return an APLized procedure that also accepts sentences:
|
1
2
3
4
5
6
7
8
|
> (define apl-sqrt (aplize sqrt))
> (apl-sqrt 36)
6
> (apl-sqrt '(1 100 25 16))
(1 10 5 4)
|
My initial answer (which I revised):
|
1
2
3
|
(define (aplize func)
(lambda (arg) (if (number? arg) (func arg) (every func arg))))
|
My second attempt at an answer (to cover the word case):
|
1
2
3
|
(define (aplize func)
(lambda (arg) (if (or (number? arg)(word? arg)) (func arg) (every func arg))))
|
This produces the desired output for apl-sqrt. i also made a procedure that appends the letter e to a single word and tested that as well. I got the expected results:
|
1
2
3
4
5
6
7
8
9
10
11
|
(define (append-e wd)
(word wd 'e))
(define apl-append-e (aplize append-e))
(apl-append-e '(ab c def g ta))
'(abe ce defe ge tae)
(apl-append-e 'potato)
'potatoe
|
AnneB’s solution is a bit more elegant. It relies on the fact that numbers return #t to word?. Anne’s version therefore doesn’t do two separate checks for both word? and number? like my version does:
|
1
2
3
4
5
6
|
(define (aplize f)
(lambda (word-or-sentence)
(if (word? word-or-sentence)
(f word-or-sentence)
(every f word-or-sentence)) ) )
|
buntine’s solution is similar to Anne’s except that buntine has the if check for whether something is a sentence:
|
1
2
3
4
5
6
|
(define (aplize f)
(lambda (n)
(if (sentence? n)
(every f n)
(f n))))
|
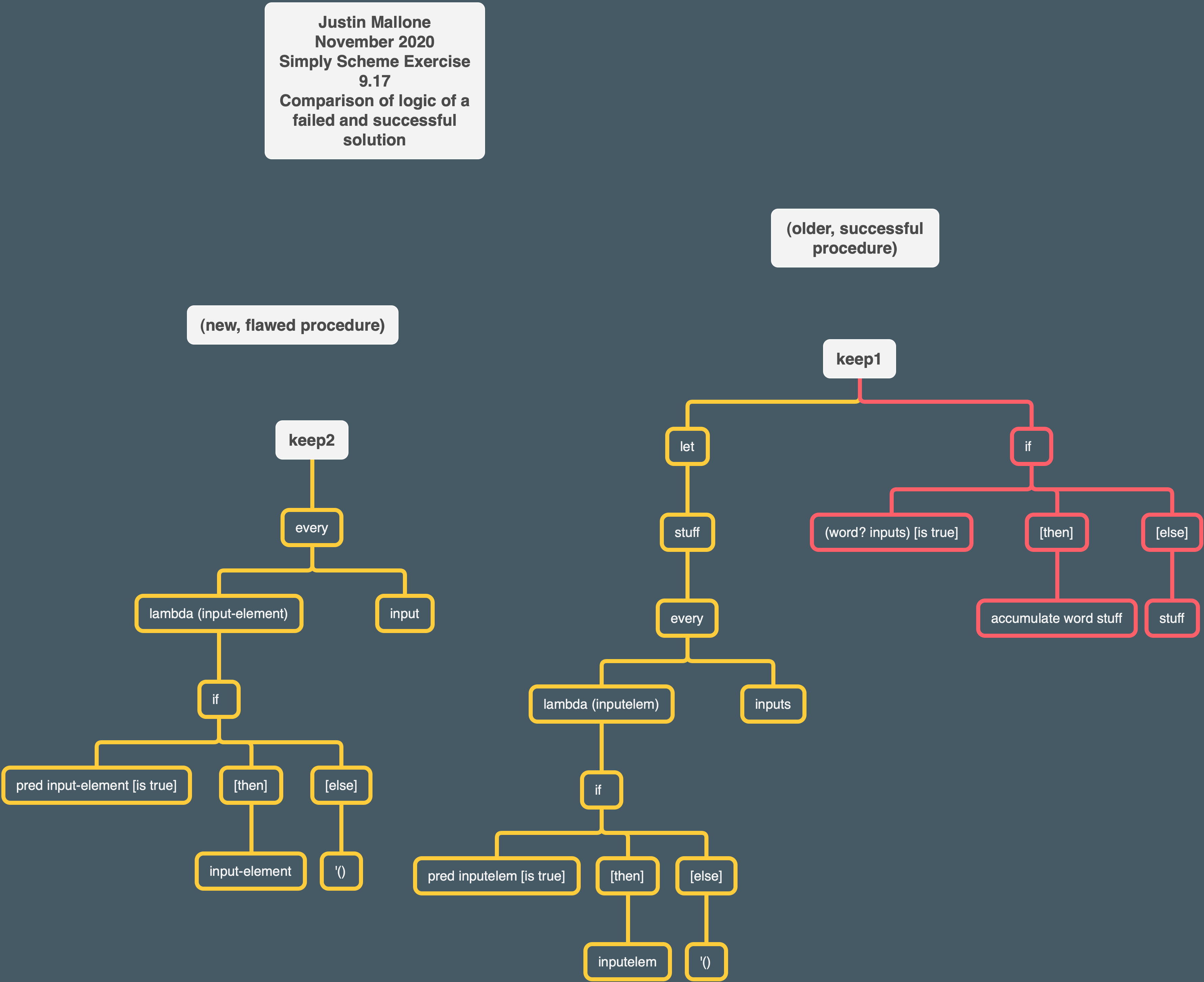
❌ Exercise 9.17
Write
keepin terms ofeveryandaccumulate
I figured out a partial solutions to this one but got a bit stuck.
|
1
2
3
|
(define (keep2 pred input)
(every (lambda (input-element) (if (pred input-element) input-element '())) input))
|
Normal keep returns the word 239 for the following input:
|
1
2
3
|
(keep number? 'zonk23hey9)
239
|
but my keep2 procedure returns '(2 3 9)
The basic way keep2 works is that the lambda takes an element and checks if the predicate procedure provided to keep is true. If so, it returns that element. If not, it returns an empty sentence. every applies this lambda procedure to each element in the input sentence. the empty sentences don’t actually appear in the final sentence produced by every.
Since I was feeling a bit stuck, I looked at an old solution of mine from a prior run through the book:
|
1
2
3
4
5
6
|
(define (keep1 pred inputs)
(let ((stuff
(every (lambda (inputelem) (if (pred inputelem) inputelem '()
)) inputs)))
(if (word? inputs) (accumulate word stuff) stuff)))
|
the lambda part is pretty similar to what I wrote above.
This program uses let to define the value of stuff as the big (every (lambda (inputelem) (if (pred inputelem) inputelem '())) inputs))) statement. It then tests whether inputs is a word. If so, it runs accumulate word on stuff. So basically, stuff has produced a sentence, and then that sentence gets accumulated into a word. Alternatively, if inputs is not a word, then stuff gets returned as a sentence.
I think I partially had trouble thinking about this solution again because I don’t have a good handle on using let yet. So maybe that is something to work on.
The functional keep1 procedure having the proper range (sentences AND words) is really important. keep2 only had sentences in its range.
Here is a tree I made comparing my flawed program with my working one: