The Little Schemer Chapter 6

Commandments

Selected Portions of Exercises

numbered?

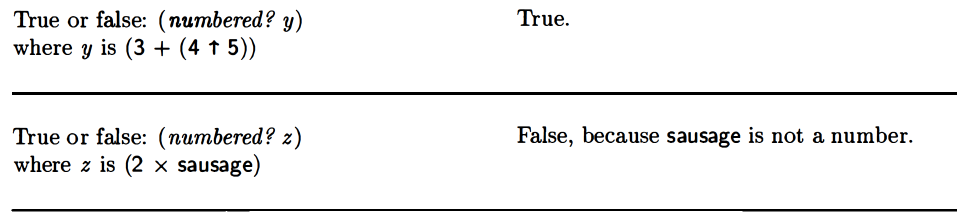
Here was my first attempt at writing numbered?

Whoops.
I’m not sure I understand. Shouldn’t we be checking for whether numbered? has any values left?

Ok so i solved this in an entirely different way than they did, lol. I can see them not using member?, I guess. member has been introduced but they haven’t really used it in solving problems, or at least not much.
Ok so … first they’re checking if aexp is an arithmetic expression, which they define as:

Note that they’re not checking if car aexp is an arithmetic expression, but if aexp is. I’m not sure I understand this check yet.
Anyways then they check whether (car (cdr aexp)) is equal to + (as an atom and not as an operator). I guess this is how they’re checking for operators. Note this check is checking the first value of the rest of the list.
I’m guessing there will be similar checks for multiplication and exponents.



Ooooh. They’re talking about abstract data types here. They’re asking questions based on the abstract data type “arithmetic expression”. I was thinking about stuff in terms of being a list.

I saw a hint from another question by accident. The hint was basically that we want to check if the atom is a number. Anyways, if aexp is down to one atom, I think we want to see if that atom is a number. The way we’ve defined an arithmetic expression, the last value for a valid arithmetic expression should be a number, since we are using infix notation here. If the last value for a would-be arithmetic expression is not a number, then we know it’s not a valid arithmetic expression.

BTW I just had the thought that, given that the data type we’re talking about uses infix expressions, that would be why the eq? checks for the operators check the first value of the rest of the list…they’re looking past the number and to the next value.

I’m still not sure of something though…it seems like we’re not addressing a key case, where we’ve got something like (potato + 4). If you run atom? on that whole thing, you’ll get false. If you check for what the second value is, everything looks okay as far as arithmetic expressions go because we’ve got a + there. But what’s going to check the value of the first thing?

Let’s look at their answer:

Ok now that I think about it I guess there has to be an else clause that covers the case I’m worried about that they have not revealed yet.

Is this new test going to be the else line? Or will this be our way of completing the eq? lines somehow?

If we assume a well-formed arithmetic expression is offered as input to numbered?, then it’s got to have an odd number of elements – either a single value like 4 or (4 + 3) which has an odd number when you count the operator.

Ok I think I’m starting to get more of the idea of how this procedure works now.

The base case is where the arithmetic expression consists of a single atom. If that’s the case, we check whether the atom is a number, returning true if it is and false otherwise.

Otherwise, we look for whether one of our operators is the second value. If we find such an operator, we recursively call numbered? twice: first, with the first value of aexp, and second, with the remainder of aexp starting with the third value of aexp (we skip over the first operator value, which is the second value). The first recursive call to numbered? for a well-formed arithmetic expression should be a single value – a number, specifically – and should return true for atom? and numbered?. The second recursive call could involve a long list and might involve more steps.

I’m a bit not sure what they’re getting at here. Let’s review a bit. numbered? was described as:

and arithmetic expressions are:

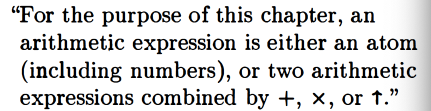
Also:

So do they want us to assume that the operators are in place and just check for numbers, or what?

Something like:

Yes that’s what they want.

value

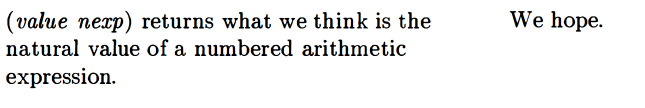
They say value asks four questions.
Here’s their first attempt at writing value:

It looks like we’re back to looking for operators here.

If we’re trying to evaluate expressions, we’re going to need to do some operations.

Well, you could deal with the (3 x 4) part separately first. Once you found it with…

…you could do (* (car nexp) (car (cdr (cdr nexp)))). Then add it up with the 1. Their answer:

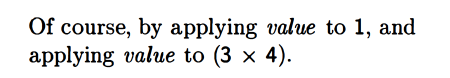
Alright so this was my attempt:

And this was their solution:

So I was sort of on the right track. One error was for the second recursive calls. Further up, I correctly said you’d want to do grab (car (cdr (cdr nexp)))) as the second value, but here I just did cdr (cdr nexp). So we’ll need to fix that.

Also, I had else be false, whereas they actually make the exponential case their else. Assuming a correct nexp as input, I think this makes sense – if we assume a correctly formed numbered expression, we just need to worry about calculating it.

I played with their version some. It handles this case correctly:

But messes up this case:

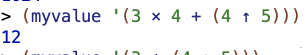
However it handles this fine:

Next subproblem:

I think the beginning would be something like this:

Let’s peek and see if I’ve got the pattern right.

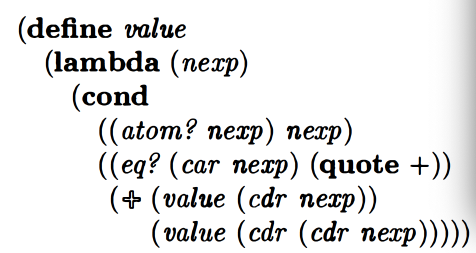
Whoops. Okay so what went wrong here.
So first I misunderstood where the
I’m not sure I see how this would work. E.g. if you give the procedure (+ 3 4) as an argument, then (cdr nexp) is (3 4) but with no operator:

Whereas with my solution you get:

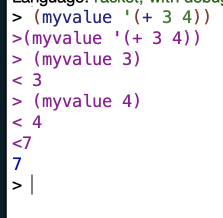
Am I misunderstanding what these expressions are supposed to look like?
Or maybe there is something later in their version of the procedure that addresses this concern.
Let’s look at the whole thing:

This is actually wrong, and my initial approach was correct. With the use of some helper procedures, here’s where the procedure winds up:

(note: an earlier version of this post neglected to include the recursive calls to myvalue within this procedure)

different representations of numbers

They want to represent numbers using groups of empty lists as numbers (so '(()()) represents 2, () represents zero, (()()()) represents 3, and so on). I covered this more in the video.

Here’s how I did addition.