Quotes from here or elsewhere in Simply Scheme unless otherwise specified. Refers to “the book” or “SS’ are to Simply Scheme.
Sometimes I show past solutions from previous attempts through the book. Those are for comparison only – I’m not really testing those like I am my current solutions.
Predicates
Boolean values in scheme are #t for true and #f for false (and #true and #false also seem to work).
A function that returns either true or false is a predicate. Some examples:
– equal?– checks if args are equal (works on numbers, sentences, procedures, words, booleans).
– member? – checks if a letter is in a word or a word is in a sentence.
– = – checks if numbers are equal.
– > – checks if one number is greater than another. Similar functions are <, >=, and <=.
– empty? – checks if for an empty sentence '() or string ""
– number? – checks if an argument is a number.
– boolean? – checks if an argument is a boolean.
– word? – checks if an argument is a word.
– sentence? – checks if an argument is a sentence.
You can also define your own predicates e.g.
|
1
2
3
4
5
6
|
(define (vowel? letter)
(member? letter 'aeiou))
(define (positive? number)
(> number 0))
|
The and, or, and not procedures, along with if, are useful to use in conjunction with predicates. The book gives some examples.
Special Forms
if, and, and or are special forms.
if doesn’t evaluate all its arguments. It only evaluates the one it needs to based on whether the first argument returns #t or not.
The rule is that if always evaluates its first argument. If the value of that argument is true, then if evaluates its second argument and returns its value. If the value of the first argument is false, then if evaluates its third argument and returns that value.
|
1
2
3
4
|
(if (= 3 3)
'sure
(factorial 1000))
|
So in the above example, if evaluates the first argument, which is (= 3 3). If and only if that returns true does it evaluate and return the second argument 'sure. If and only if the first argument returns false does it evaluate (factorial 1000).
and and or are also special forms which evaluate their arguments from left to right. or stops and returns a true value as soon as it hits a true argument, and and stops and returns false as soon as it hits a false argument.
Semipredicates
SS says every value is considered true except #f. This fact allows us to have semipredicates. The book doesn’t actually formally define what a semipredicate is in this chapter. But I think that predicates are procedures that return either true or false, and semipredicates seem to be procedures that can return either false or a true value other than just#t or #true.
🤔 Integer-quotient and Some Confusion
There was a passage that I had some trouble understanding. This might be a bit rambly so maybe skip it if you’re just quickly skimming.
#Tisn’t the only true value. In fact, every value is considered true except for#f.
|
1
2
3
4
|
> (if (+ 3 4) 'yes 'no)
YES
|
This allows us to have semipredicates that give slightly more information than just true or false. For example, we can write an integer quotient procedure. That is to say, our procedure will divide its first argument by the second, but only if the first is evenly divisible by the second. If not, our procedure will return
#f.
SS then gives the following example (i’ve added the divisible procedure below, which was defined earlier in the chapter, as necessary context)
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
|
(define (divisible? big small)
(= (remainder big small) 0))
(define (integer-quotient big little)
(if (divisible? big little)
(/ big little)
#f))
> (integer-quotient 27 3)
9
> (integer-quotient 12 5)
#F
|
So backing up, I thought that, in the part that says…
This allows us to have semipredicates that give slightly more information than just true or false.
…that the “this” referred to the fact that…
every value is considered true except for
#f
…which I will refer to herein as the Truth-Fact. Based on that interpretation, I expected the Truth-Fact to be a necessary part of how the first version of integer-quotient works. I now think that maybe they were actually referring to the Truth-Fact being necessary for the revised version that they describe later in the section, though, but I’m not sure.
I read the procedure above this way: divisible is a necessary helper procedure. It relies on the = procedure, which returns #t if the remainder is 0 and #f if the remainder is something other than 0. The divisible? procedure called within the first argument of the if will return #t if the remainder of the first argument passed into integer-quotient is 0 when divided by the second argument. In that case, the check by the if procedure that its first argument is true will succeed, and the second argument will be evaluated and the quotient returned. If divisible? returns false, however, then the third argument to the if – the #f – will be returned.
With that description of the procedure in mind, I don’t see how the Truth-Fact plays a role in the version of integer-quotient above. I get that integer-quotient meets what I laid out as my definition of a semipredicate, but whether something is a semipredicate seems different than whether it relies on the Truth-Fact for its operation.
and and or also semipredicates. The book mentions that or will return the first true result:
|
1
2
3
|
> (or #f 3 #f 4)
3
|
3 has a truth value of #t. or doesn’t return that #t, but the value itself.
and works the following way:
|
1
2
3
|
> (and 1 2 3 4 5)
5
|
If all the arguments given to and are true, it returns the value of the last argument.
Of the fact that and returns the value of the last argument when all the arguments given to and are true, the book says the following:
As an example in which this behavior is useful, we can rewrite integer-quotient more tersely:
|
1
2
3
4
|
(define (integer-quotient big little) ;; alternate version
(and (divisible? big little)
(/ big little)))
|
With this example, I can easily see how the Truth-Fact is necessary to how it works. Specifically, the programmer is relying on the fact that the numeric value of (/ big little) will return as true (for the and) and return as the value that the procedure outputs. When the first argument to the and (the (divisible? big little)) is returned as true, the programmer wants the second argument to be the value that is returned by invocation the procedure. and will return the final value when both arguments are true, and so the number returned by (/ big little) being true is necessary for this function to work in the way the programmer wants it to.
Cond
cond provides a concise way of handling situations where you have to choose from among multiple possibilities.
|
1
2
3
4
5
6
7
8
9
10
|
(define (roman-value letter)
(cond ((equal? letter 'i) 1)
((equal? letter 'v) 5)
((equal? letter 'x) 10)
((equal? letter 'l) 50)
((equal? letter 'c) 100)
((equal? letter 'd) 500)
((equal? letter 'm) 1000)
(else 'huh?)))
|
To take one example, for ((equal? letter 'i) 1), (equal? letter 'i) is the condition that gets tested, and 1 is the thing that gets returned if the condition is true. So each cond clause like this is analogous to the first two arguments after an if clause. But with cond you get to have a whole series of alternatives rather than just specifying one like you can in if, and each alternative can have its own condition, unlike in if where you’re just testing the first argument.
cond is a special form and doesn’t evaluate arguments until it needs to.
Re: else:
By convention, the last argument always starts with the word
elseinstead of an expression. You can think of this as representing a true value, butelsedoesn’t mean true in any other context; you’re only allowed to use it as the condition of the last clause of acond.
The book emphasizes that one should put the most restrictive test first in a cond statement. Pasting this as images cuz of a formatting issue on the web page:

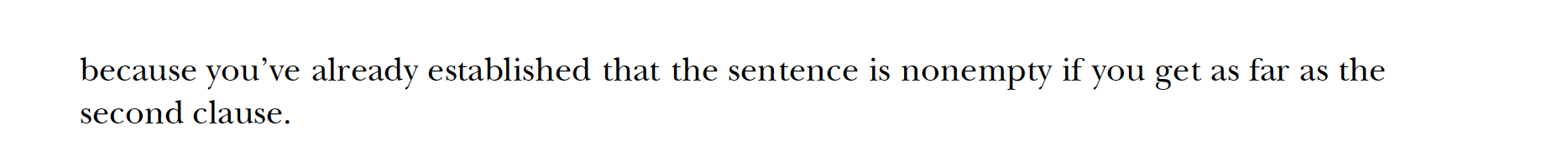
Why is (empty? sent) more restrictive than (number? (first sent))? I think because (empty? sent) will only return true on an empty sentence, whereas (number? (first sent)) will return true on infinitely many potential sentences. So (empty? sent) rules out all sentences but one, whereas (number? (first sent)) will return true for many sentences. Another way of saying it is that (empty? sent) is trying to find out whether we’re dealing with a sentence with content at all, whereas (number? (first sent))is trying to get some information about what sort of non-empty sentence we’re dealing in within the universe of non-empty sentences.
The book emphasizes that the values returned by if can be used as part of larger functions, consistent with Scheme’s overall approach. E.g. this works:
|
1
2
3
4
5
6
7
|
(define (greet name)
(se '(pleased to meet you)
(if (equal? (first name) 'professor)
(se 'professor (last name))
(first name))
'(- how are you?)))
|
Boring Exercises
Exercise 6.1
✅ Exercise 6.1.1
What values are printed when you type these expressions to Scheme? (Figure it out in your head before you try it on the computer.)
|
1
2
3
4
|
(cond ((= 3 4) '(this boy))
((< 2 5) '(nowhere man))
(else '(two of us)))
|
This returns '(nowhere man), as I expected.
❌ Exercise 6.1.2
|
1
2
3
4
|
(cond (empty? 3)
(square 7)
(else 9))
|
I misread how cond and this program work. I expected it to return 49 for some reason – I think that I thought the first line would have (empty?) evaluate 3 and return #f, and so then (square 7) would evaluate and return the true value 49. What actually happened was that the program returned 3.
The book actually has a relevant example. Let me reread that:
Don’t get into bad habits of thinking about the appearance of
condclauses in terms of “two parentheses in a row.” That’s often the case, but not always. For example, here is a procedure that translates Scheme true or false values (#tand#f) into more human-readable wordstrueandfalse.
|
1
2
3
4
5
6
7
8
9
10
|
(define (truefalse value)
(cond (value 'true)
(else 'false)))
> (truefalse (= 2 (+ 1 1)))
TRUE
> (truefalse (= 5 (+ 2 2)))
FALSE
|
So what is happening? In this example, when the value is something that evaluates to #t, the 'true is returned. The value, despite not being a complex expression like ((equal? letter 'i) 1), has a truth value, and so when cond sees that that value is true, it then proceeds to return the “consequent”, which in this case is the word 'true.
In all other cases, truefalse returns the wordfalse.
I think the point is thatcond can, but need not have, a sub-expression as the first value which gets checked for its truth value. It can be a simple expression like value above. Or a procedure like empty?! Since basically everything in Scheme is true, empty? has a truth value too..

So in the cond for this exercise, empty? gets evaluated as true, and so the consequent 3 gets returned as a result.
✅ Exercise 6.1.3
|
1
2
3
4
5
6
7
|
(define (third-person-singular verb)
(cond ((equal? verb 'be) 'is)
((equal? (last verb) 'o) (word verb 'es))
(else (word verb 's))))
(third-person-singular 'go)
|
This returns goes.
✅ Exercise 6.2
What values are printed when you type these expressions to Scheme? (Figure it out in your head before you try it on the computer.)
✅ Exercise 6.2.1
|
1
2
|
(or #f #f #f #t)
|
This returns #t.
✅ Exercise 6.2.2
|
1
2
|
(and #f #f #f #t)
|
This returns #f.
✅ Exercise 6.2.3
|
1
2
|
(or (= 2 3) (= 4 3))
|
✅ Exercise 6.2.4
|
1
2
|
(not #f)
|
This returns #t.
✅ Exercise 6.2.5
|
1
2
|
(or (not (= 2 3)) (= 4 3))
|
This returns #t.
✅ Exercise 6.2.6
|
1
2
|
(or (and (= 2 3) (= 3 3)) (and (< 2 3) (< 3 4)))
|
this returns #t.
✅ Exercise 6.3
Rewrite the following procedure using a
condinstead of theifs:
|
1
2
3
4
5
6
7
|
(define (sign number)
(if (< number 0)
'negative
(if (= number 0)
'zero
'positive)))
|
Answer:
|
1
2
3
4
5
|
(define (sign number)
(cond ((< number 0) 'negative)
((= number 0) 'zero)
(else 'positive)))
|
✅ Exercise 6.4
** Rewrite the following procedure using an
ifinstead of thecond:
|
1
2
3
4
|
(define (utensil meal)
(cond ((equal? meal 'chinese) 'chopsticks)
(else 'fork)))
|
Answer:
|
1
2
3
|
(define (utensil meal)
(if (equal? meal 'chinese) 'chopsticks 'fork))
|
Real Exercises
✅ Exercise 6.5
Write a procedure
european-timeto convert a time from American AM/PM notation into European 24-hour notation. Also writeamerican-time, which does the opposite:

Answer:
|
1
2
3
4
5
6
7
8
9
10
11
12
|
(define (european-time us-time)
(cond ((equal? us-time '(12 am)) '24)
((equal? us-time '(12 pm)) '12)
((equal? (first (bf us-time)) 'am) (first us-time))
(else (+ 12 (first us-time)))))
(define (american-time euro-time)
(cond ((= euro-time 24)'(12 AM))
((= euro-time 12)'(12 PM))
((< euro-time 12)(se euro-time 'AM))
(else (se (- euro-time 12) 'PM))))
|
NOTE: for ((equal? (first (bf us-time)) 'am) (first us-time)), replacing (first (bf with last, like AnneB does in her implementation, would be better…
Past Solution
Old answer, from a previous time I did the book:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
|
<br />(define (european-time americantime)
(cond ((and (equal? (first americantime)12)(member? 'a (last americantime)))'24)
((and (equal? (first americantime)12)(member? 'p (last americantime)))'12)
(else (+ (first americantime)
(if (member? 'p (last americantime))12 0)
))))
(define (american-time europeantime)
(cond ((= europeantime 24)'12am)
((> europeantime 12)(word (- europeantime 12)'pm))
((< europeantime 12)(word europeantime 'am))
(else (word europeantime 'pm))))
|
For european-time, I think checking for whether the entire input is equal? to the us-time for the special cases of 12am and 12pm makes way more sense and is much more elegant and readable than the stuff i did last time with member? etc.
✅ Exercise 6.6
Write a predicate
teen?that returns true if its argument is between 13 and 19.
Answer:
|
1
2
3
|
(define (teen? age)
(if (and (>= age 13)(<= age 19)) #t #f))
|
AnneB points out that the if statement is not necessary and this can be represented as:
|
1
2
3
|
(define (teen? age)
(and (> age 12) (> 20 age)))
|
Past Solution
Last time I went through Simply Scheme I did the following for this problem:
|
1
2
3
|
(define (teen? age)
(member? age '(13 14 15 16 17 18 19)))
|
This works but would scale up really badly if you wanted to do a similar sort of thing but with a larger range of numbers.
✅ Exercise 6.7 – Troubleshooting Scheme 🧐
Write a procedure
type-ofthat takes anything as its argument and returns one of the wordsword,sentence,number, orboolean:
|
1
2
3
4
5
6
7
8
9
|
> (type-of '(getting better))
SENTENCE
> (type-of 'revolution)
WORD
> (type-of (= 3 3))
BOOLEAN
|
For this program I had to change the Scheme file I was using. I had to do this cuz the sentence? procedure was returning erroneous results.
I had been using this file https://gist.github.com/alexgian/5b351f367169b40a4ad809f0bb718e1f
And I had been using this declaration at the beginning of my Scheme files:

(I kept the simply_redef.scm file in a definitions subfolder in each place where I was storing .scm files).
For this exercise, I switched to using this declaration:
![]()
This caused sentence? to perform as expected 🙂
So with that out of the way, my actual answer to the exercise:
|
1
2
3
4
5
6
7
|
(define (type-of input)
(cond ((number? input) 'NUMBER)
((sentence? input) 'SENTENCE)
((word? input) 'WORD)
((boolean? input) 'BOOLEAN)
(else '(WHAT ARE YOU?!))))
|
test inputs:
|
1
2
3
4
5
6
7
|
(type-of '(getting better))
(type-of 'revolution)
(type-of (= 3 3))
(type-of 5)
(type-of #t)
(type-of empty?)
|
outputs:
|
1
2
3
4
5
6
7
|
'SENTENCE
'WORD
'BOOLEAN
'NUMBER
'BOOLEAN
'(WHAT ARE YOU?!)
|
✅ Exercise 6.8
Write a procedure
indef-articlethat works like this:
|
1
2
3
4
5
6
|
> (indef-article 'beatle)
(A BEATLE)
> (indef-article 'album)
(AN ALBUM)
|
Don’t worry about silent initial consonants like the
hinhour.
Answer:
|
1
2
3
4
5
|
(define (vowel? x) (member? x '(a e i o u)))
(define (indef-article wd)
(if (vowel? (first wd)) (se 'an wd) (se 'a wd)))
|
✅ Exercise 6.9
Sometimes you must choose the singular or the plural of a word:
1 bookbut2 books. Write a procedurethismanythat takes two arguments, a number and a singular noun, and combines them appropriately:
|
1
2
3
4
5
6
|
> (thismany 1 'partridge)
(1 PARTRIDGE)
> (thismany 3 'french-hen)
(3 FRENCH-HENS)
|
In the court of doing this assignment, I greatly improved plural.
Answer. plural is where the interesting action is happening here. Note: some of the options in the upper-right of the code window may help with readability.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
|
(define (plural wd)
(cond
((equal? (word (last (bl wd))(last wd)) 'is)(word (bl (bl wd))'es)) ;words ending in is
((member? (word (last (bl wd))(last wd)) '(sh ch)) (word wd 'es)) ;words ending in sh or ch
((member? (word (last (bl wd))(last wd)) '(ay ey iy oy)) (word wd 's)) ;words ending in a vowel plus y, exlcuding uy, which is treated differently and covered under the general rule for words ending in y
((equal? (last wd) 'y) (word (bl wd) 'ies)) ;words ending in y
((member? (last wd) '(s x z)) (word wd 'es)) ; words ending in s, x, or z
(else (word wd 's))))
(define (thismany num wd)
(if (> num 1)
(se num (plural wd))
(se num wd)))
|
✅ Exercise 6.10
Write a procedure
sort2that takes as its argument a sentence containing two numbers. It should return a sentence containing the same two numbers, but in ascending order:
|
1
2
3
4
5
6
7
|
> (sort2 '(5 7))
(5 7)
> (sort2 '(7 5))
(5 7)
|
answer:
|
1
2
3
4
5
|
(define (sort2 num-sent)
(if (> (first num-sent)(first (bf num-sent)))
(se (first (bf num-sent))(first num-sent))
num-sent))
|
Again I weirdly don’t make use of last.
❌ Exercise 6.11
NOTE: caught an error in this program after posting and changed the ✅ to an ❌. I discuss the error here
Write a predicate
valid-date?that takes three numbers as arguments, representing a month, a day of the month, and a year. Your procedure should return#tif the numbers represent a valid date (e.g., it isn’t the 31st of September). February has 29 days if the year is divisible by 4, except that if the year is divisible by 100 it must also be divisible by 400.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
|
> (valid-date? 10 4 1949)
#T
> (valid-date? 20 4 1776)
#F
> (valid-date? 5 0 1992)
#F
> (valid-date? 2 29 1900)
#F
> (valid-date? 2 29 2000)
#T
|
I defined a program that looked for violations of the date rules and returned false if it found a violation, but returned true otherwise. I’ve included versions with both no comments and comments in case the commented version has readability issues. Note: some of the options in the upper-right of the code window may help with readability.
no comments:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
|
(define (divisible? big small)
(= (remainder big small) 0))
(define (valid-date? month day year)
(cond
((and (= month 2)
(or
(> day 29)
(and (= day 29)(divisible? year 100) (not (divisible? year 400)))
(and (= day 29)(not (divisible? year 4))
(and (> day 28)))))
#f)
((and (member? month '(4 6 9 11))(> day 30)) #f)
((not (and (>= day 1)(<= day 31))) #f)
((not (and (>= month 1)(<= month 12))) #f)
(else #t)))
|
with comments:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
|
(define (divisible? big small)
(= (remainder big small) 0))
(define (valid-date? month day year)
(cond
((and (= month 2) ; this first cond is February logic, which is the most complex. if month = 2...
(or ; ...and any of the following are true...
(> day 29) ; ... day > 29, which should never be the case, or...
(and (= day 29)(divisible? year 100) (not (divisible? year 400))) ; ...day = 29 AND year is divisible by 100 but NOT divisible by 400, which is a situation prohibited by a special leap year rule or....
(and (= day 29)(not (divisible? year 4)) ; ....day is = 29 and year is NOT divisible by 4, which is prohibited by the general leap year rule, or....
(and (> day 28))))) ; ....day > 28, which is prohibited by the rule for February in general
#f) ; ... then return false
((and (member? month '(4 6 9 11))(> day 30)) #f) ; if month is 4, 6, 9, or 11 AND day is greater than 30 return false.
((not (and (>= day 1)(<= day 31))) #f) ; day should always be greater than or equal to 1 and less than or equal to 31, regardless of month or year (some months are more restrictive on the number of days, but those are addressed above). If that is NOT the case, return false. This line imposes the limit of 31 days for the 31-day months.
((not (and (>= month 1)(<= month 12))) #f) ; month should always be greater than or equal to 1 and less than or equal to 12. If that is NOT the case, return false.
(else #t)))
|
AnneB addressed some issues related to year-validity that I didn’t.
Past Solution 1
Here’s an earlier attempt of mine at solving this problem.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
|
(define (divisible? num divisor)
(equal? (remainder num divisor)0))
(define (leap-check day year)
(if (divisible? year 100)
(if (divisible? year 400) #T #F)
(if (divisible? year 4) #T #F)))
(define (feb-checker day year)
(cond ((and (= day 29)(leap-check day year)))
((< day 29))
(else #f)))
(define (valid-date? month day year)
(cond ((< day 1)#F)
((< month 1)#F)
((< year 1)#F)
((equal? month 2) (feb-checker day year))
((and (member? month '(1 3 5 7 8 10 12))(< day 32)))
((and (member? month '(4 6 9 11))(< day 31)))
(else #f)))
|
The organization seems solid. I like how concise my current solution is though.
✅ Exercise 6.12
Make
pluralhandle correctly words that end inybut have a vowel before they, such asboy. Then teach it about words that end inx(box). What other special cases can you find?
I did this in an earlier problem.
I’ll do it clean here without the comments
|
1
2
3
4
5
6
7
8
9
|
(define (plural wd)
(cond
((equal? (word (last (bl wd))(last wd)) 'is)(word (bl (bl wd))'es))
((member? (word (last (bl wd))(last wd)) '(sh ch)) (word wd 'es))
((member? (word (last (bl wd))(last wd)) '(ay ey iy oy)) (word wd 's))
((equal? (last wd) 'y) (word (bl wd) 'ies))
((member? (last wd) '(s x z)) (word wd 'es))
(else (word wd 's))))
|
AnneB‘s does more cases than mine does!
✅ Exercise 6.13
Write a better
greetprocedure that understands as many different kinds of names as you can think of:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
|
> (greet '(john lennon))
(HELLO JOHN)
> (greet '(dr marie curie))
(HELLO DR CURIE)
> (greet '(dr martin luther king jr))
(HELLO DR KING)
> (greet '(queen elizabeth)
(HELLO YOUR MAJESTY)
> (greet '(david livingstone))
(DR LIVINGSTONE I PRESUME?)
|
Answer. My remove-post-nominal-letters procedure handles a bunch of cases like the
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
|
(define (remove-post-nominal-letters name)
(if (member? (last name)'(jr Jr Junior junior Sr sr Senior senior II ii III iii IV iv ESQ Esq esq PHD Phd phd))
(bl name)
name))
(define (greet name)
(cond
((equal? name '(david livingstone))'(dr livingstone i presume?))
((equal? name '(donald trump))'(Hello Mr President))
((equal? (first name) 'queen)'(Hello your majesty))
((member? (first name)'(dr doctor Doctor Dr Professor professor senator Senator governor Governor))
(se 'hello (first name) (last (remove-post-nominal-letters name))))
(else (se 'hello (first name)))))
|
Note: my previous work on this problem in past attempts didn’t deal with the MLK jr case at all.
I really like how buntine organized his solution here with the helper procedures.
✅ Exercise 6.14
Write a procedure
describe-timethat takes a number of seconds as its argument and returns a more useful description of that amount of time:
|
1
2
3
4
5
6
7
8
9
|
> (describe-time 45)
(45 SECONDS)
> (describe-time 930)
(15.5 MINUTES)
> (describe-time 30000000000)
(9.506426344208686 CENTURIES)
|
answer:
|
1
2
3
4
5
6
7
8
9
10
11
|
(define (describe-time seconds)
(cond ((> seconds 3153600000)(se (/ seconds 3153600000)'centuries))
((> seconds 315360000)(se (/ seconds 315360000)'decades))
((> seconds 31536000)(se (/ seconds 31536000)'years))
((> seconds 2592000)(se (/ seconds 2592000)'months))
((> seconds 604800)(se (/ seconds 604800)'weeks))
((> seconds 86400)(se (/ seconds 86400)'days))
((> seconds 3600)(se (/ seconds 3600)'hours))
((> seconds 60)(se (/ seconds 60)'minutes))
(else (se seconds 'seconds))))
|
Reflections
I should use the composability if if more to make stuff more concise.
I should consider using helper procedures more than I do.
I should think about whether procedures I’ve already built earlier in the chapter or elsewhere might be helpful with making later procedures (as AnneB did with exercise 6.14).

