How to Define a Procedure
Essential aspects of defining a procedure, with an example:
|
1
2
3
|
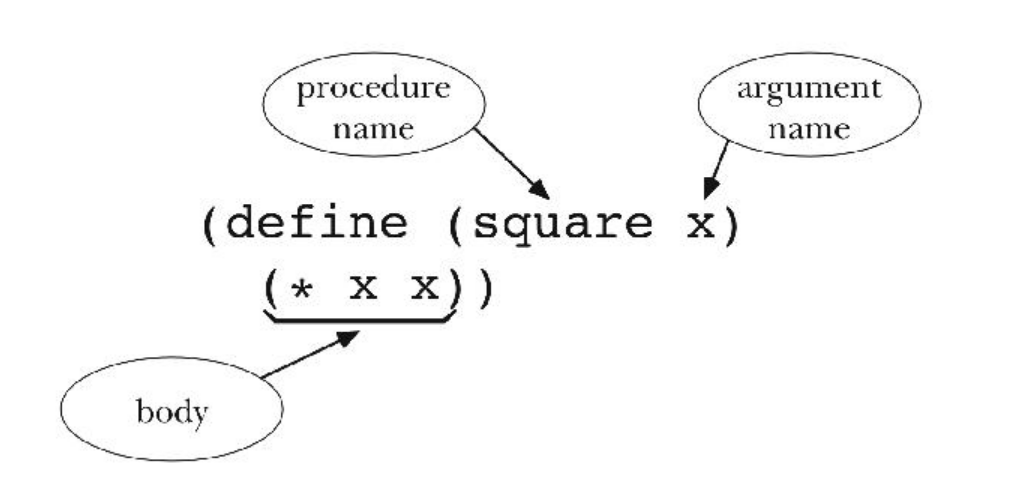
(define (square x)
(* x x))
|
- The word
define, which indicates that you are defining something. - The name you want to give the procedure.
- The name(s) you want to give its argument(s).
- Body: what the procedure actually does. “an expression whose value provides the function’s return value.”
Special Forms
define is an example of a special form. Special forms have their own evaluation rules. For define in our square example, none of the parts got evaluated, which is different than how Scheme normally treats expressions. Normally, Scheme evaluates sub-expressions and then evaluates the whole expression once the sub-expressions have been evaluated. But that wouldn’t make sense to do with define.
define isn’t actually a procedure at all in a technical sense. But as a simplification, the book discusses define as if it is a procedure, unless there is some important reason not to.
Functions and Procedures
Function — an association between the starting value(s) and the resulting value, no matter how that result is computed. The same function can be represented by different operations.
The book notes that there is a distinction between a function and a procedure, and that functions can be represented in different ways (such as a table that represents the relationship between US States and state capitals; I also came up with the example of coordinates that indicate a certain location on a map – the coordinates are the starting value, the specific location on a map is a return value, and the relationship between coordinates and locations is represented by the map, and might even be represented three-dimensionally by a globe).
Argument Names versus Argument Values
Formal parameter – what you call an argument as defined in a function. E.g. for…
|
1
2
3
|
(define (square x)
(* x x))
|
the formal parameter is x. It’s a placeholder value for an actual argument.
Actual argument expression – an expression that serves as the actual argument for a procedure.
Actual argument value – the specific value that a procedure receives in a case when it is invoked.
Example: for (square (+ 5 9)), (+ 5 9) is the actual argument expression, and the actual argument value is 14.
Substitution Model
Today’s story is about the substitution model. When a procedure is invoked, the goal is to carry out the computation described in its body. The problem is that the body is written in terms of the formal parameters, while the computation has to use the actual argument values. So what Scheme needs is a way to associate actual argument values with formal parameters. It does this by making a new copy of the body of the procedure, in which it substitutes the argument values for every appearance of the formal parameters, and then evaluating the resulting expression. So, if you’ve defined
squarewith
|
1
2
3
|
(define (square x)
(* x x))
|
then the body of
squareis(* x x). When you want to know the square of a particular number, as in(square 5), Scheme substitutes the 5 forxeverywhere in the body of square and evaluates the expression. In other words, Scheme takes
|
1
2
|
(* x x)
|
then does the substitution, getting
|
1
2
|
(* 5 5)
|
and then evaluates that expression, getting 25.
Shorter Points
Abstracting out a pattern and giving it a name is important. It lets you deal with certain problems without having to worry about the details.
Composition of functions is the basis for all Scheme programming.
Pitfalls
Functions can only have one return value. If you return multiple values, Scheme will ignore earlier ones and return the last one.
Don’t use the name of a procedure as a formal parameter. If you use the same name with two meanings within the same procedure (as e.g. parameter and procedure) it will cause a problem.
Similar issue as above: don’t use the name of a keyword (such as define) as some other kind of name.
Don’t try to write a procedure that has a complex expression as a formal parameter.
|
1
2
3
|
(define (f (+ 3 x) y) ;; wrong!
(* x y))
|
Questions
- In what important cases, if any, does
definenot being a “real” procedure make a difference?
Exercises
✅ Exercise 4.1
Show the substitution that occurs when you evaluate
|
1
2
3
4
5
6
7
8
9
|
(define (ho-hum 8 12) ; step 1
(+ 8 (* 2 12)))
(define (ho-hum 8 12) ; step 2
(+ 8 24))
(define (ho-hum 8 12) ; step 3
32)
|
✅🤔Exercise 4.2
Given the following procedure:
|
1
2
3
|
(define (yawn x)
(+ 3 (* x 2)))
|
list all the little people that are involved in evaluating
|
1
2
|
(yawn (/ 8 2))
|
Substituting the parameter in:
|
1
2
|
(+ 3 (* (/ 8 2) 2)))
|
(Give their names, their specialties, their arguments, who hires them, and what they do with their answers.)
There are three little people. I’ll give them names (like in a prior exercise) and say what they do.
- Adam is a
yawnspecialist and hires everyone else. Yawn takes the(/ 8 2)expression and substitutes it into the body ofyawn. He has nobody that he reports to. - Bob is an addition specialist. His arguments are 3 (given directly) and 8 (given by Charlie). The result is 11, and this is reported to Adam.
- Charlie is a multiplication specialist. His arguments are 4 (given by Donald) and 2 (given directly). The result is 8. This result is reported to Bob.
- Donald is a division specialist. His arguments are 8 and 2 (both given directly). The result is 4, and this resulted is reported to Charlie.
Note: AnneB talks about a “head boss” who hires the yawn specialist. This tracks how the book talked about this. I’m unclear whether this is an important detail or whether the book was just trying to be colorful with the hiring metaphor.
✅ Exercise 4.3
Here are some procedure definitions. For each one, describe the function in English, show a sample invocation, and show the result of that invocation.
Note: I edited some of these for a mistaken use of “parameter” in place of “argument”.
✅ 4.3.1
|
1
2
|
(define (f x y) (- y x))
|
This procedure finds the difference between the two arguments provided; specifically, it takes the second argument and subtracts the first argument from it.
A sample invocation:
|
1
2
3
|
> (f 5 8)
3
|
✅ 4.3.2
|
1
2
|
(define (identity x) x)
|
This procedure returns as a result whatever is provided as the argument. Sample invocations:
|
1
2
3
4
5
6
7
8
9
|
> (identity 'apple)
'apple
> (identity 'potato)
'potato
> (identity 12)
12
> (identity every)
#<procedure:every>
|
✅ 4.3.3
|
1
2
|
(define (three x) 3)
|
This procedure takes an argument but just returns 3, regardless of the argument provided.
|
1
2
3
4
5
6
7
|
> (three 'potato)
3
> (three every)
3
> (three 15)
3
|
✅ 4.3.4
|
1
2
|
(define (seven) 7)
|
This procedure does not take an argument. It merely defines the name seven as 7.
|
1
2
3
|
> (seven)
7
|
✅ 4.3.5
|
1
2
3
4
5
6
7
|
(define (magic n)
(- (/ (+ (+ (* 3 n)
13)
(- n 1))
4)
3))
|
This procedure takes a number argument and performs a series of arithmetical operations on the number which result in the same number being returned.
the number n is multiplied by 3, added to 13, added to the difference of itself and 1, divided by 4, and then has 3 subtracted.
So for example, 10 is multiplied by 3, producing 30.
It’s then added to 13, producing 43.
It’s added to (10 – 1), so now it’s 52.
It’s divided by 4, so it’s now 13.
Then 3 is subtracted, so it’s back to 10.
Sample invocation:
|
1
2
3
|
> (magic 10)
10
|
Note: AnneB actually did the math to make sure this function always returns the given argument. 👍
✅ Exercise 4.4
Each of the following procedure definitions has an error of some kind. Say what’s wrong and why, and fix it:
✅ 4.4.1
|
1
2
3
4
|
(define (sphere-volume r)
(* (/ 4 3) 3.141592654)
(* r r r))
|
As written, this expression is trying to return multiple values, and so the earlier value is getting ignored. What the programmer wants to do is multiply these values together. This can be accomplished by deleting the ) to the right of the 3.141592654. Fixed:
|
1
2
3
4
|
(define (sphere-volume r)
(* (/ 4 3) 3.141592654
(* r r r))
|
✅ 4.4.2
|
1
2
3
|
(define (next x)
(x + 1))
|
This one is using infix notation but Scheme uses prefix notation.
|
1
2
3
|
(define (next x)
(+ x 1))
|
✅ 4.4.3
|
1
2
3
|
(define (square)
(* x x))
|
This one forgot to give square a formal parameter.
|
1
2
3
|
(define (square x)
(* x x))
|
✅ 4.4.4
|
1
2
3
|
(define (triangle-area triangle)
(* 0.5 base height))
|
This doesn’t designate “base” or “height” as the formal parameters, but uses them in the body anyways. Thus these are just undefined terms and Scheme doesn’t know what to do with them. One possible fix:
|
1
2
3
|
(define (triangle-area base height)
(* 0.5 base height))
|
✅ 4.4.5
|
1
2
3
|
(define (sum-of-squares (square x) (square y))
(+ (square x) (square y)))
|
This is using complex expressions for the formal parameters. This is trying to do some of the job of the procedure invocation stage at the definition stage.
instead do this:
|
1
2
3
|
(define (sum-of-squares x y)
(+ (square x) (square y)))
|
and if you want to square the arguments, just do something like:
|
1
2
|
(sum-of-squares (square 4) (square 5))
|
✅ Exercise 4.5
Write a procedure to convert a temperature from Fahrenheit to Celsius, and another to convert in the other direction. The two formulas are F=9⁄5C+32 and C=5⁄9(F-32).
|
1
2
3
|
(define (fahrenheit-to-celsius fahrenheit-temp)
(* 5/9 (- fahrenheit-temp 32)))
|
|
1
2
3
|
(define (celsius-to-fahrenheit celsius-temp)
(+ 32 (* 9/5 celsius-temp)))
|
✅ Exercise 4.6
Define a procedure
fourththat computes the fourth power of its argument. Do this two ways, first using the multiplication function, and then usingsquareand not (directly) using multiplication.
Way 1:
|
1
2
3
|
(define (fourth number)
(* number (* number (* number (* number)))))
|
Note: AnneB’s solution is better, as she makes use of the fact that * takes multiple arguments, so the result is more elegant.
Way 2:
|
1
2
3
|
(define (fourth number)
(square (square number)))
|
✅ Exercise 4.7
Write a procedure that computes the absolute value of its argument by finding the square root of the square of the argument.
|
1
2
3
|
(define (absolute-value number)
(sqrt (square number)))
|
✅ Exercise 4.8
Note that I changed the formatting of the exponents cuz I don’t think Ulysses does superscript.
“Scientific notation” is a way to represent very small or very large numbers by combining a medium-sized number with a power of 10. For example, 5 x [10^7] represents the number 50000000, while 3.26×[10^-9] represents 0.00000000326 in scientific notation. Write a procedure
scientificthat takes two arguments, a number and an exponent of 10, and returns the corresponding value:
|
1
2
3
4
5
6
|
> (scientific 7 3)
7000
> (scientific 42 -5)
0.00042
|
Some versions of Scheme represent fractions in a/b form, and some use scientific notation, so you might see
21/50000or4.2E-4as the result of the last example instead of0.00042, but these are the same value.
Solution for scientific:
|
1
2
3
|
(define (scientific number power-of-ten)
(* number (expt 10 power-of-ten)))
|
❌ Harder Probem for Hotshots
(A harder problem for hotshots: Can you write procedures that go in the other direction? So you’d have
|
1
2
3
4
5
6
|
> (sci-coefficient 7000)
7
> (sci-exponent 7000)
3
|
You might find the primitive procedures
logandfloorhelpful.)
I could not figure out how to use log and floor effectively.
After trying for a while and writing the stuff about getting unstuck at the end of the post, I started reading Anne’s answer. I’m taking the approach I talk about later in the post of seeing “if it’s possible to do ‘partial spoilers’, like get a hint from someone or only read the beginning of an answer, so you can get unstuck while still figuring some things out.”
Anne says:
I wrote these as a first try:
(define (sci-exponent n)
(floor (log n)))(define (sci-coefficient n)
(/ n (expt 10 (sci-exponent n))))But I saw that in my program, log returns the natural log, not the base 10 log.
Yeah okay, I did get as far as noticing that.
I looked in the DrRacket documentation and saw that if you give a second argument to log then it’s supposed to use the second argument as a base.
Ah! I’m gonna add “check the documentation” to a list of things at the end of the post.
More AnneB:
That did not work in my version—it said it expected one argument and not two.
I searched some more and found this, which shows how to get a base 10 log:
Here’s the usual way to do that.
(define (log10 n) (/ (log n) (log 10)))
(log10 100)
2.0
Ah so that’s interesting. I came across something like this as well. I think I didn’t read it cuz I wanted to try to figure out the problem using the stuff I’d already learned from the book. That’s a bit silly though. After you’ve been stuck for a while, it’s worth trying out different things. It’s possible that if I’d checked the documentation like Anne did and had seen how log was supposed to work, I would have been more open to trying different things.
With the very big hint re: the log10 stuff and Anne’s other discussion so far, I was able to write procedures successfully:
|
1
2
3
4
5
6
7
8
9
10
|
(define (log10 n)
(/ (log n) (log 10)))
(define (sci-exponent number)
(floor (log10 number)))
(define (sci-coefficient number)
(/ number (expt 10 (sci-exponent number))))
|
Let me try to explain what each part is doing. Warning – I try to explain math stuff a bit so this might be a little muddled.
log10 is dividing the natural logarithm of the argument number by the natural logarithm of 10. In math, there is something called the change of base formula.

Suppose you want to evaluate the logarithm of a number in some base that isn’t on a calculator or that you don’t have a built-in programming language function for figuring out. The change of base formula lets you evaluate the logarithm of some number in whatever base you want. The first step is to find the logarithm of the number in whatever base you have access to a logarithm function for. Recall that log in Scheme finds the natural logarithm. Then we divide by the logarithm of the base we actually want to use(again, in whatever base we have access to, which for Scheme is the natural logarithm).
I found an example:


So for our case, mathematically, we want to find the natural logarithm of some number and then divide that by the natural logarithm of 10. That is what the log10 function accomplishes.
If we get call log10 on 7300, we get 3.8633228601204554. That is the power we would have to raise 10 to in order to get 7300. That makes sense, since raising 10 to 3 gets us 1000 and raising 10 to 4 gets us 10,000, so the value for 7300 has to be within 3 and 4.
3.8633228601204554 isn’t a great number for the purposes of sci-exponent though. The purpose of sci-exponent is to tell us what power of 10 we’d have to raise 10 to so that (10 raised to some power) multiplied by some coefficient will produce some number. We know that 10^3 is 1000 and 10^4 is 10,000. 3.8633228601204554 is a long number with a lot of stuff after the decimal cuz it needs to raise 10 to 7300. One way to think about things is that the 3 gets the 10 to 1000 and the .8633228601204554 gets us the rest of the way to 7300. But for the purposes of sci-exponent we’re just interested in the 3 (or whatever whole number exponent) and not interested in the stuff after the decimal. Think of the number 7300. One way of representing it is 7.3 x 1000. The coefficient part of scientific notation is the part on the left – the 7.3. The purpose of sci-exponent is to figure out the value on the right – and specifically to figure it out in exponential form (as in, 10 to what power produces the value on the right).
We know that scientific notation involves a coefficient and an exponent combining to concisely express a large or small number. If we took the log10 of some number and rounded up, and then tried to multiply the result from doing that with the coefficient, we’d get the incorrect answer. For example, if we rounded 3.8633228601204554 up to 4, and then multiplied that by 7.3, we’d get 73000. So for the purposes of figuring out sci-exponent, we want to always be rounding the log10 down. That is what floor accomplishes – it rounds down to the next integer.
sci-coefficient simply divides the number by 10 raised to the sci-exponent of the number. This produces the coefficient, as you would expect.
Some test cases and results:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
|
> (sci-coefficient 0.00042)
4.2
> (sci-coefficient 0.034)
3.4000000000000004
> (sci-coefficient 7300)
7.3
> (sci-coefficient 1.05)
1.05
> (sci-exponent 7000)
3.0
> (sci-exponent 7300)
3.0
> (sci-exponent 1.05)
0.0
> (sci-exponent 0.00042)
-4.0
|
✅ Exercise 4.9
Define a procedure discount that takes two arguments: an item’s initial price and a percentage discount. It should return the new price:
(discount 10 5)
9.50(discount 29.90 50)
14.95
|
1
2
3
|
(define (discount original-price percentage-reduction)
(- original-price (* original-price (/ percentage-reduction 100))))
|
Note: AnneB‘s version is more elegant because she just multiplied original-price, 0.01 and what i call percentage-reduction together, rather than doing more nesting and dividing by 100.
✅ Exercise 4.10
Write a procedure to compute the tip you should leave at a restaurant. It should take the total bill as its argument and return the amount of the tip. It should tip by 15%, but it should know to round up so that the total amount of money you leave (tip plus original bill) is a whole number of dollars. (Use the ceiling procedure to round up.)
(tip 19.98)
3.02(tip 29.23)
4.77(tip 7.54)
1.46
|
1
2
3
|
(define (tip bill)
(- (ceiling (* 1.15 bill)) bill))
|
One caveat: the (tip 19.98) test case produces some kind of rounding error that can be replicated doing other simple arithmetic operations like (- 23 20.98). AnneB had this issue as well.
Troubleshooting an Instance of Getting Stuck
I got stuck on the “harder problem for hotshots” from Exercise 4.8. I’m going to write some thoughts about that. I broke the thoughts up into two categories: 1) stuff that I think is more about how to approach getting stuck in general and 2) stuff that seems more specific to getting unstuck while doing programming.
Getting Unstuck in General
- Consider the time-based metric for overreaching. I went way over 15 minutes being stuck this time.
- when thinking of time-based metric for overreaching, consider setting an actual timer once you realize you are getting stuck. Give yourself e.g. 15 minutes to get unstuck, and if the timer goes off, just move on with other parts of the project/life. It’s very easy for me (and I bet for other people) to get caught in biased “I just need five more minutes to figure this out” loops, so external checks/alerts like a timer can help with that. (This is a bit like the gambler who thinks things will turn around on the next roll of the dice. The fact that sometimes things do turn around doesn’t make this approach any less of a bad strategy – you gotta think about things in terms of expected return instead of focusing on outlier outcomes).
- Consider alternate uses of time within the project – e.g. consider whether it is worth spending an hour being stuck when you could just read the answer and move on and actually learn more stuff.
- Consider alternate “meta” uses of time – e.g. it might be way more valuable to spend an hour writing learning methodology troubleshooting analysis like this rather than spend it on being stuck.
- Think about motivation for spending time on thing you’re getting stuck on – e.g. do I wanna solve the problem for “hotshots” cuz I want to be a “hotshot”? Second-handedness issue there maybe…
- Think about immediate importance of resolving issue – e.g. if it’s a problem for “hotshots” then that’s an indicator there might not be a strong expectation you can solve the problem right now, so you’re not “behind” or failing or anything, so you don’t need to worry about that.
- If it’s something with an “answer”, see if it’s possible to do “partial spoilers”, like get a hint from someone or only read the beginning of an answer, so you can get unstuck while still figuring some things out yourself.
- Review past thoughts/notes regarding learning methodology.
- Try to have a big picture perspective regarding how the project is going rather than focusing in on one part that you got stuck on and making that a major issue in your mind.
- Ask for help!
Programming Project Troubleshooting
- Specify in detail all your project requirements – e.g. what test cases are you expecting the program to have to solve?
- Specify in detail all assumptions, restrictions, limitations that seem important and relevant to what you are stuck on — e.g. I was trying to limit how I approached the problem I got stuck on by only using functions that had already been meaningfully introduced – so no recursion or
cond. That’s a big limitation that’s worth explicitly stating, at least. - If any of the information or advice from the problem seems unusable or irrelevant, at least say so and say what you did to try to figure out whether it was relevant or not — e.g. I couldn’t figure out how to use
floororlogin the problem I got stuck on, but didn’t really go into detail about what I had tried or thought of in terms of how I might use them. - Check the documentation – AnneB discovered that
logis supposed to work in a certain way by checking the docs. - Get super organized –
- make sure your attempted solutions are nicely formatted.
- do detailed commenting on what each part does.
- keep track of each problem solving attempt rather than deleting it. This will let people help you more effectively by showing them how you’re thinking about the problem.
- make sure your attempted solutions are nicely formatted.
Review of Past Learning Attempts
This is the first chapter I have some substantial work from the past to review.
Something worthy of note is that I basically did not get anywhere with sci-coefficient and sci-exponent the last time around, though I did figure out scientific. I seemed to have solve the other problems in a very similar manner.
Learning Methodology
I set a goal for this chapter to try to ask more explicit questions but wound up getting very side-tracked with the getting stuck thing. However, I thought I wrote some good thoughts about that topic, so that seems okay.
Regarding the Getting Unstuck in General section: Sometimes, especially with a math or programming problem, when I’m not getting anywhere, I put the problem aside and come back to it the next day. Often, I’ve thought of new approaches to try by then.