Tag: Simply Scheme

Follow-up On Simply Scheme Chapter 1 Notes

Learning Methodology Problems from Chapter 1 Notes

  • Lack of trees.
  • Lack of explicitly writing down enough questions.
    • Need to take every part of the program seriously – everything is there for a reason, presumably. What is the reason?
  • Lack of going step-by-step enough (did this somewhat but could do better).
  • Not taking advantage of the interactivity of the interactions window of DrRacket enough. Need to play with things more!
  • Moving forward while still being fuzzy on stuff.
  • Trying to go through stuff too quickly.

Things to focus on improving for this post:
1. Go step by step more
2. Test stuff more
3. Make a tree

Going More Step by Step on the Ice Cream Choices Example

Got stuck in my attempt to understand this one, so seemed worth doubling back.

If Statements

This procedure has an if statement. Can I actually write one of those on my own? Let me try it (using an expression from Roman history)

Here are some very simple examples of if from a Scheme guide which I’m bookmarking now 🙂:

it also describes the general form of the syntax:

Note that you don’t need to expressly introduce the alternative with an else or something like that.

Let me make my own if statement.

It actually took me a couple tries to get the syntax and parentheses correct. Probably a strong indicator that testing my understanding of writing if in Scheme was a good idea!

I get the expected output from this.

Let Contrasted with Define & Lambda

Earlier I said:

I got a little confused trying to figure out what let does and how it’s different than lambda. I don’t wanna get stuck in the mud by jumping the gun (intentional mixed metaphor 😉 ) so I won’t worry too much about this for now. It seems like let is kind of similar to lambda, except with lambda you don’t give the temporary function a name and with let you can (or have to? Not sure).

I found this article which contrasts let and define and I found the comparison helpful.

Following the advice on that page, I first used define in the interactions window.
Here’s what they showed should happen:

And here’s what happened for me:

Pretty close! I’m missing the line with #<unspecified> and just have a blank line there instead.

The article says

This shows that even once used, the variable x continues to exist, it is defined for all to see, use and (as we shall see later on) modify at will.

The value of the x as 2 persists once it is defined as 2.

They contrast let with this:

If I enter the following statement in the interactions window:

I get 8

But if I try to get the value of x again:

Notice here, how once the block of code has finished executing, the variables x and y are no longer accessible.

ERRONEOUS ❌: You also can’t just define something in a let and return the value.

ERRONEOUS ❌:let expects a procedure. If you evaluate (+) by itself, it returns zero, and so if you use it with just one number, it returns that number.

CORRECTION: let expects a procedure above because of the parentheses around the final x. You actually can define a let and just return a value:

Thanks to AnneB for pointing this mistake out!

So if we did want to just get the same value x value out of let for some reason in the above example, we could do:

Which gives us 2. I don’t know why one might want to do such a thing, but it could be done.

The article also contrasts the general form of the two expressions let and define:

In general, the form of a define statement for a variable is as follows:
(define <variable name> <variable value>)

…

In general, the form of a let statement is as follows:
(let ((var1 val1) ... (varn valn)) (<body>))

With let, you actually use the variables to perform some operation immediately and then the values of the variables are no longer available. Given that, it makes sense that you would have to say what that operation is immediately within the let statement. Whereas with define, because the assignment of a value to a variable persists, we can assign some variable a value and then use it whenever later on.

In my last post I said:

It seems like let is kind of similar to lambda, except with lambda you don’t give the temporary function a name and with let you can (or have to? Not sure).

With let, it does look like you have to assign something a value and then do something with it.

I was thinking of the difference between let, lambda, and define, and how to try to put the difference in an easy-to-grasp way. If this isn’t quite right then hopefully someone will say it’s wrong and I can correct it 🙂

With define, you give some value to a name and use it to do stuff later on. The value could be a word, a number, or a function. And you can refer back to that value with the name you gave it later cuz you’ve defined it in a lasting way.

❗️CLARIFICATION: You can actually use define in a non-lasting way that only works temporary within a function:

this program will print pizza if the program is called, but the variable bestfood is not accessible from outside the program. Thanks to AnneB for pointing this out.

With let, you give some name to a value in order to do stuff right now. You do your stuff within the let expression.

With lambda, you skip the whole naming part and just start immediately doing stuff (though you do have to specify what you’ll be doing stuff to.)

Map

In my previous post I said:

every applies a function that follows it to each word in a sentence. map applies a function that follows it to each item in a list.

Let’s see what this actually means in practice with a simple example.

This returns (5).

This returns '(5 7). This is the behavior I would expect so far.

Reduce

In my previous post I said:

reduce is similar to the accumulate function used in the Acronyms example. Accumulate “takes a procedure and a sentence as its arguments. It applies that procedure to two of the words of the sentence.” Chapter 17 of Simply Scheme says that “Reduce is just like accumulate except that it works only on lists, not on words.”

Therefore…

…returns 26, unsurprisingly.

and this:

returns 'lalalala. Note that if you just give (la la la la) to word, it does not work, because word doesn’t expect a list.

So you really need the reduce here.

Append

As I said in my last post, append append makes a list out of the elements of lists provided as arguments.

So:

produces '(New York New Jersey Connecticut) in a single, flattened list with no nested list structure.

What if the lists you are trying to append are double-nested?

this produces
'((New York) (New Jersey) (Connecticut)), where the elements are in a single list, but within that list, they are only nested once.

Car & Cdr

car selects the first element of a list. So for (car '(New York New Jersey Connecticut)) it returns 'New and for (car '((New York)(New Jersey)(Connecticut)))  it returns '(New York).

cdr selects all but the first elements in a list. So for (cdr '(New York New Jersey Connecticut)) it returns '(York New Jersey Connecticut) and for (cdr '((New York)(New Jersey)(Connecticut))) it returns '((New Jersey) (Connecticut)), as I would expect.

What happens if you cdr a list with only one element? For example, what happens when you cdr a list with only nested list?

You get an empty list.

Lambda

I think I should play around with lambda a bit more as well.

If we just do:

We get back a procedure object.

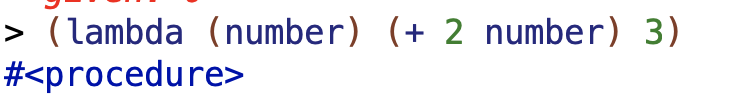
That’s because we haven’t actually applied the procedure to anything yet. If we want to actually apply the procedure to something, we need to give it some input to serve as the number:

Note the highlighting:

So what we’re doing in the above is generating our procedure object (with the lambda in the highlighted part), and them giving Scheme something to apply that object to (the 3).

Prepend-every – Combining Map & Lambda

Now I’ll start trying to combine the different parts I’ve talked about to build up to a larger procedure.

First let’s try map and lambda. Part of the choices program draws upon a helper function prepend-every, which uses map and lambda, so that seems like a good test case.

I talked about prepend-every a bit in my last post.

I saw that it prepends an item to each element of a list. For example:

So how does this function work, in detail?

Let’s look at a different version of the function first.

prepend-every-nomap has had the map removed and the parentheses adjusted accordingly. What value will this give us when we run it?

So rather than prepend apple to each element of the list, it prepends apple to the whole list. Why?

map is the thing in the original prepend-every procedure that tells the lambda of prepend-every to access each element of the list lst. Without map providing this instruction, prepend-every-nomap just treats the entire list lst as one unit and runs the lambda procedure on it. The lambda procedure takes the item and the lst and makes a sentence out of them. In the original prepend-every, I think that choice stands for the individual element of a list being selected at that moment by map for combination with the item in the lambda function. But in prepend-every-nomap, choice brings in the entire lst.

All this shows the role of map in the prepend-every function and how it can operate together with lambda. map can enable a lambda function to do a whole lot more than it might be able to otherwise.

Putting Things Together

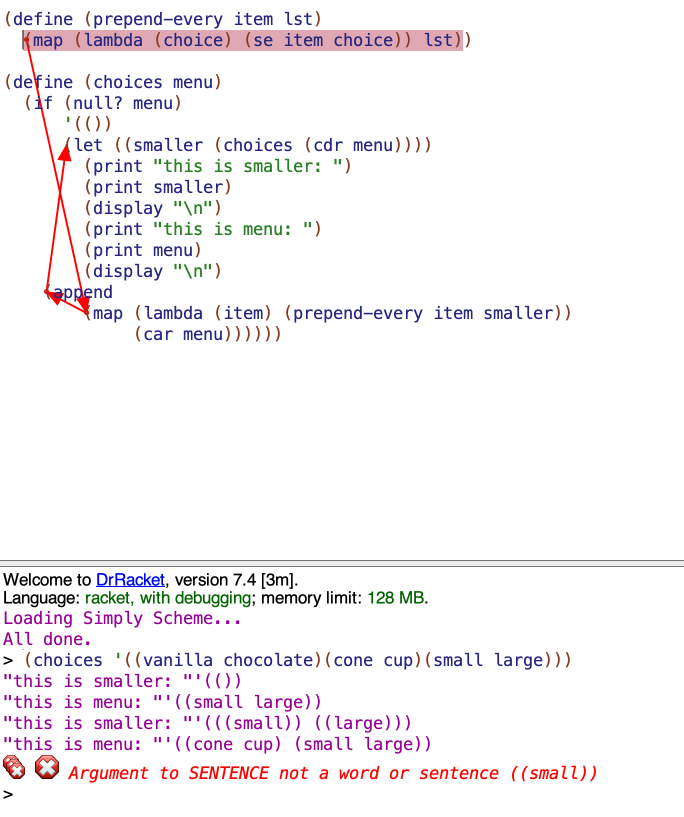
I made a version of the choices procedure with print statements for smaller and menu (and newlines to clean things up) in order to get a better idea of what was going on:

I ran the above with (choices '((vanilla chocolate)(cone cup)(small large))) as the input and got the following back:

So here is my attempt to explain this:

  • When the number of nested lists being provided as the menu gets down to 1, then when the (let ((smaller (choices (cdr menu)))) line tries to get the cdr of that menu, it will not return an entry but an empty list, as described in the Car & Cdr section above. We actually specify that the program return a nested empty list on (null? menu) and not just an empty list. I’m not 100% on the reasoning for that.
  • When we get to the point where (cdr menu) returns our empty nested list, we still have an entry in our menu list – in my example, we have '(small large). So I think what happens is that when we get down to the base case, smaller is an empty nested list (()). Then we go through the (map (lambda (item) (prepend-every item smaller))(car menu)))))) part of the program. The map goes through each element of (small large) – so small and large respectively – and applies the lambda function. The lambda function takes small as an item and then prepends small to the empty nested list that the let has given the name smaller. The lambda function then goes through next item provided by map, large, and does the same, prepending it to an empty nested list. The result of this process is this line:
  • The format of '((small) (large)) poses somewhat of a problem, because we’re not done processing the information from our choices list at this stage. We need to use the information from '((small) (large)) at a “higher level” of the sequence of recursive calls that the choices procedure makes. But here we run into a problem. I tried to demonstrate the problem by removing the reduce from the program full choices program:

  • So what exactly is going on here? prepend-every operates by combining some item with a list using the sentence-former se. Without reduce and append working together to flatten the structure of the lists generated by the running of the choices procedure, prepend-every ultimately winds up getting handed a nested list, ((small)), which it doesn’t know what to do with. reduce append serves to keep the lists from getting so nested that they cause a problem for prepend-every. This allows the program to function as a whole and generate our desired result.

Questions

  1. Is there a reason that we have the return on (null? menu) be a nested list? There must be, because if you change it to just an empty list, the program returns an empty list.

Learning Methodology Review

I accomplished the goals I wanted to in terms of learning methodology. I went step by step, tested out lots of stuff, and made a tree. I found the step by step and testing stuff out things very helpful. In particular, I think I made some gains in the skill of figuring out how to test stuff, which seems important. I think the print statements I used in the “Putting Things Together” section are a good example of this.

I also made a tree. I am not sure how much the tree helped. I think maybe it helped a bit with understanding the structure of the program, but I think testing out the individual parts of the program helped way more with that.

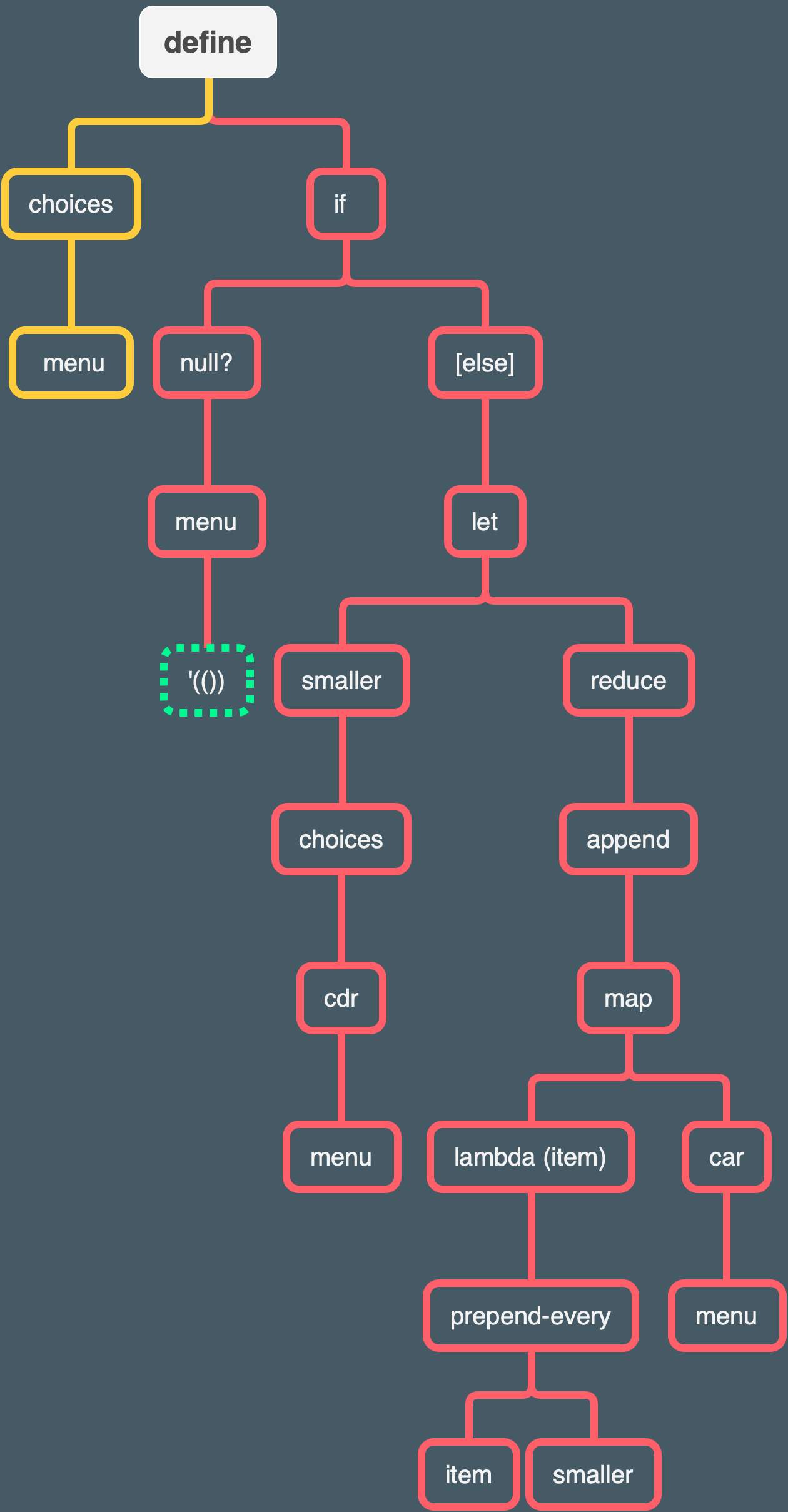
Tree

Here is my attempt at a tree for the choices procedure.