Commandments
Selected Portions of Exercises


rember-f

How do you write rember-f? My attempt:
|
1
2
3
4
5
6
7
8
9
|
(define myrember-f
(lambda (test? a l)
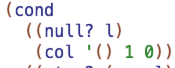
(cond
((null? l)'())
((test? (car l) a)
(cdr l))
(else (cons (car l)
(myrember-f test? a l))))))
|
They agreed.
lambdas

Some work I did to understand this:
This returns a procedure that checks whether an argument x is equal to “hat”:

And these pass the arguments “hat” and “cat” to that argument, respectively, returning the appropriate value:

rewriting rember-f

My answer:
|
1
2
3
4
5
6
7
8
9
10
|
(define myrember-f
(lambda (test?)
(lambda (a l)
(cond
((null? l)'())
((test? (car l) a)
(cdr l))
(else (cons (car l)
((myrember-f test?) a (cdr l))))))))
|
I had to think about the recursive case, and providing the test? argument to the recursive invocation.
insertL-f

This was insertL from a previous chapter:
|
1
2
3
4
5
6
7
8
9
10
11
12
|
(define insertL
(lambda (new old lat)
(cond
((null? lat) '())
(else
(cond
((eq? (car lat) old)
(cons new lat))
(else
(cons (car lat)
(insertL new old (cdr lat)))))))))
|
Here’s an intermediate version:
|
1
2
3
4
5
6
7
8
9
10
|
(define myinsertL-f
(lambda (test? new old lat)
(cond
((null? lat) '())
((test? (car lat) old)
(cons new lat))
(else
(cons (car lat)
(myinsertL-f test? new old (cdr lat)))))))
|
And here is the final version:
|
1
2
3
4
5
6
7
8
9
10
11
|
(define myinsertL-f
(lambda (test?)
(lambda (new old l)
(cond
((null? l) '())
((test? (car l) old)
(cons new l))
(else
(cons (car l)
((myinsertL-f test?) new old (cdr l))))))))
|
Note the two changes: test? is put in a separate lambda, and is also grouped with myinsertL-f in the recursive call.
Theirs is basically the same.
insertR-f
![]()
This was insertR from earlier:
|
1
2
3
4
5
6
7
8
9
10
|
(define insertR
(lambda (new old lat)
(cond ((null? lat) '())
(else
(cond
((eq? (car lat) old)
(cons old (cons new (cdr lat))))
(else (cons (car lat)
(insertR new old (cdr lat)))))))))
|
And this is my insertR-f:
|
1
2
3
4
5
6
7
8
9
10
|
(define myinsertR-f
(lambda (test?)
(lambda (new old l)
(cond
((null? l) '())
((test? (car l) old)
(cons old (cons new (cdr l))))
(else (cons (car l)
((myinsertR-f test?) new old (cdr l))))))))
|
They agreed.
insert-g

My initial attempt:
|
1
2
3
4
5
6
7
8
9
10
11
|
(define insert-g
(lambda (new old l insert)
(cond ((null? l) '())
((equal? (car l) old)
(cond
((eq? insert 'l)
(cons new (cons old (cdr l))))
(else (cons old (cons new (cdr l))))))
(else (cons (car l)
(insert-g new old (cdr l) insert))))))
|

This is what I attempted at this point before reading further:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
|
(define insertleft
(lambda (new old l)
(cons new (cons old (cdr l)))))
(define insertright
(lambda (new old l)
(cons old (cons new (cdr l)))))
(define myinsert-g
(lambda (new old l f)
(cond ((null? l) '())
((equal? (car l) old)
(f new old l))
(else (cons (car l)
(myinsert-g new old (cdr l) f))))))
|
They take a similar approach to my second one above:


You can solve insert-g the same with their seqL and seqR procedures, the only difference being that you pass in cdr l to the function instead of l directly:
|
1
2
3
4
5
6
7
8
|
(define theirinsert-g
(lambda (new old l f)
(cond ((null? l) '())
((equal? (car l) old)
(f new old (cdr l)))
(else (cons (car l)
(theirinsert-g new old (cdr l) f))))))
|
They wind up writing insert-g as an argument of one argument seq which is either seqL or seqR:

![]()
|
1
2
3
4
5
6
7
8
9
10
11
12
13
|
(define theirinsert-g
(lambda (f)
(lambda (new old l)
(cond ((null? l) '())
((equal? (car l) old)
(f new old (cdr l)))
(else (cons (car l)
((theirinsert-g f) new old (cdr l))))))))
(define mynewinsertL
(theirinsert-g seqL))
|
![]()
|
1
2
3
|
(define mynewinsertR
(theirinsert-g seqR))
|

We’re using a function-creating function to define arbitrary functions in terms of that function, which is something we haven’t done before.
Also, since our function-creating function returns a function that itself takes arguments, we don’t need to use a lambda in our definition.
They had a different point in mind:


|
1
2
3
|
(define mynewerinsertL
(theirinsert-g (lambda (new old l) (cons new (cons old l)))))
|
Their version works the same.
subst

![]()
|
1
2
3
4
|
(define seqsubst
(lambda (new old l)
(cons new l)))
|
|
1
2
3
|
(define mysubst
(theirinsert-g seqsubst))
|
mystery function yyy & seqrem

I’m a bit confused about this. The first thing I’m confused about is what role seqrem is performing exactly. Stuff like seqL actually performed some operation, but looking at it, seqrem just seems to return the list.
Ok thinking about it more, invoking insert-g with seqrem returns a procedure with seqrem in place of f in the body of insert-g. So we have a seqrem function that just returns the list argument its passed whenever the car l is equal to old:
|
1
2
3
4
5
6
7
8
9
10
|
(define insert-g
(lambda (f)
(lambda (new old l)
(cond ((null? l) '())
((equal? (car l) old)
(seqrem new old (cdr l)))
(else (cons (car l)
((theirinsert-g seqrem) new old (cdr l))))))))
|
We see seqrem returning the list it’s passed in this trace result:
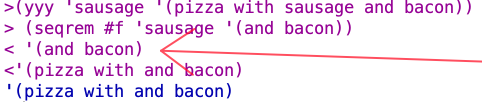
seqrem is returning ‘(and bacon) because sausage is the value that returns true for the equal? line, and so the list at that point is ‘(sausage and bacon), and so the cdr l at that point is ‘(and bacon).
The (and bacon) value gets the preceding values (excluding the value we want to remove, which is skipped) cons‘ed on to it by the invocations of the procedures at higher levels of the chain of recursive invocations. And thus we get ‘(pizza with and bacon).
atom-to-function
In the context of discussing the value procedure from chapter 6, they ask the following:

My answer:
|
1
2
3
4
5
6
7
8
|
(define atom-to-function
(lambda (x)
(cond ((eq? x '+)
+)
((eq? x '×)
×)
(else ↑))))
|

I initially erred in thinking about this, cuz I wasn’t thinking about what operator would do.
So nexp gets passed into operator, which returns the atom '+. That atom gets passed in as the argument to atom-to-function, which returns a function which performs addition.
multirember-f

My attempt:
|
1
2
3
4
5
6
7
8
9
10
|
(define multirember-f
(lambda (f?)
(lambda (a l)
(cond
((null? l) '())
((f? (car l) a)
((multirember-f f?) a (cdr l)))
(else (cons (car l)
((multirember-f f?) a (cdr l))))))))
|
Their solution is essentially the same.
![]()
|
1
2
3
|
(define multirember-eq?
(multirember-f eq?))
|
multirember-T

My solution:
|
1
2
3
4
5
6
7
8
9
|
(define multiremberT
(lambda (f? lat)
(cond
((null? lat) '())
((f? (car lat))
(multiremberT f? (cdr lat)))
(else (cons (car lat)
(multiremberT f? (cdr lat)))))))
|
Their version is essentially the same.
multirember&co
Initial Problem



Initially, null? lat is false, so we skip to the next line.
(eq? (car lat) a) is true, so we recursively invoke multirember&co with 'tuna as a, () (or the current (cdr lat) as lat.
a-friend is used by the lambda procedure to generate a new argument which becomes the col for the recursive call. This new argument is a function of two arguments which invokes a-friend. The first argument given to a-friend within this function is the cons of car lat (which is currently tuna) and the argument newlat. The second argument is the argument seen.
null? lat is true within the recursive call, so we invoke our col procedure – the function of two arguments involving a-friend– on two empty lists. The following represents the operation of the lambda function in the base case:
![]()
Another Problem
Next problem:

I found a stackoverflow discussion on this procedure which I found helpful. I talked about this a bunch of the video. I found this post, which was linked in the discussion, very helpful, along with the top stackoverflow answer and the one with the flowcharts.
Initial Call to multirember&co
a: tuna
lat: (and tuna)
col: a-friend
(and tuna) is not null, and (car lat) of it (and) isn’t equal to tuna, so we go to the else clause. We pass in ‘tuna as the new a and (tuna) as the new lat, respectively.
As the new col, we pass in a procedure. Let’s call this procedure z1. z1 conses ‘and onto the first argument taken by the procedure, which is newlat. The result of this consing serves as the first argument to a-friend. The second argument taken by z1, seen, is passed to a-friend directly.
|
1
2
3
4
|
(define z1
(lambda (newlat seen)
(a-friend (cons 'and newlat) seen)))
|
First Recursive Call
a: tuna
lat: (tuna)
col: z1
Within the first recursive call, lat is still not null (it’s (tuna) now), so we go to the eq? line. (car lat) is eq? to tuna, so we make another recursive call. The arguments to this new recursive call will be tuna as a, the empty list as lat, and what we’ll call z2 as col.
What does z2 consist of? A function of two arguments that invokes z1 and conses tuna onto seen.
|
1
2
3
4
|
(define z2
(lambda (newlat seen)
(z1 newlat (cons 'tuna seen))))
|
Second Recursive Call
a: tuna
lat: ‘()
col: z2
Within the second recursive call to multirember&co, the lat is empty, so the null? lat condition returns true. Since that is the case, we then pass z2 two empty lists. This ultimately leads to the procedure returning #f, because by the time the arguments we cons values onto get back to a-friend, the second argument is not null:

Yet Another Problem

In general, multirember&co works as follows:
– if car lat is equal to the a, then car lat gets cons‘ed onto the second argument.
– Otherwise, car lat gets cons‘ed onto the first argument.
This col checks the length of the first argument passed to it. Only one of the elements of the lat is equal to a, so the final arguments being passed to last-friend will be (strawberries and swordfish) for the first argument and (tuna) for the second argument. So the value returned will be 3.
They agree. Whew!
multiinsertLR


My answer:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
|
(define multiinsertLR
(lambda (new oldL oldR lat)
(cond
((null? lat) '())
((eq? (car lat) oldL)
(cons new
(cons oldL
(multiinsertLR new oldL oldR (cdr lat)))))
((eq? (car lat) oldR)
(cons oldR
(cons new
(multiinsertLR new oldL oldR (cdr lat)))))
(else (cons (car lat)
(multiinsertLR new oldL oldR (cdr lat)))))))
|
Question: if oldL and oldR are the same, should we add new on both sides? Apparently the authors don’t think so, cuz their version was essentially the same as mine.
multiinsertLR&co



|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
|
<br />(define multiinsertLR&co
(lambda (new oldL oldR lat col)
(cond
((null? lat)
(col '() 0 0))
((eq? (car lat) oldL)
(multiinsertLR&co new oldL oldR (cdr lat)
(lambda (newlat L R)
(col (cons new
(cons oldL newlat))
(add1 L) R))))
((eq? (car lat) oldR)
(multiinsertLR&co new oldL oldR (cdr lat)
(lambda (newlat L R)
(col (cons oldR (cons new newlat))
L (add1 R)
))))
(else (cons (car lat)
(multiinsertLR&co new oldL oldR (cdr lat)
(lambda (newlat L R)
(col (cons (car lat) newlat) L R))))))))
|

Step 1
new: salty
oldL: fish
oldR: chips
lat: (chips and fish or fish and chips)
lat is not null.
car lat is not equal to oldL.
It is, however, equal to oldR.
We therefore recursively invoke multiinsertLR&co. The procedure we use, which I’ll call q1, is as follows (note that I’m using list as the col function:
|
1
2
3
4
5
|
(define q1
(lambda (newlat L R)
(list (cons 'chips (cons 'salty newlat))
L (add1 R))))
|
If we use q1 on the empty list and two 0’s that we get when the lat is null we get the following:

A good start!
Step 2
new: salty
oldL: fish
oldR: chips
lat: (and fish or fish and chips)
lat is not null and (car lat) matches neither our oldL nor oldR. We therefore go to the else and recursively invoke our multiinsertLR&co procedure with the following function serving as col:
|
1
2
3
4
|
(define q2
(lambda (newlat L R)
(q1 (cons 'and newlat) L R)))
|
![]()
Step 3
new: salty
oldL: fish
oldR: chips
lat: (fish or fish and chips)
lat is not null and (car lat) matches oldL so we recursively invoke our multiinsertLR&co with the following function serving as col:
|
1
2
3
4
|
(define q3
(lambda (newlat L R)
(q2 (cons 'salty (cons 'fish newlat)) (add1 L) R)))
|

Step 4
new: salty
oldL: fish
oldR: chips
lat: (or fish and chips)
lat is not null and car lat is not equal to oldL or oldR so we go to the else clause and recursively invoke multiinsertLR&co with the following function serving as col:
|
1
2
3
4
|
(define q4
(lambda (newlat L R)
(q3 (cons 'and newlat) L R)))
|

Step 5
new: salty
oldL: fish
oldR: chips
lat: (fish and chips)
lat is not null but is equal to oldL so we recursively invoke multiinsertLR&co with the following as the col:
|
1
2
3
4
|
(define q5
(lambda (newlat L R)
(q4 (cons 'salty (cons 'fish newlat)) (add1 L) R)))
|

Step 6
new: salty
oldL: fish
oldR: chips
lat: (and chips)
lat is not null and (car lat) is not equal to oldL or oldR so we recursively invoke multiinsertLR&co with the following as the col:
|
1
2
3
4
|
(define q6
(lambda (newlat L R)
(q5 (cons 'and newlat) L R)))
|
![]()
Step 7
new: salty
oldL: fish
oldR: chips
lat: (chips)
lat is not null and (car lat) is equal to oldR so we recursively invoke multininsertLR&co with the following as the col:
|
1
2
3
4
5
|
(define q7
(lambda (newlat L R)
(q6 (cons 'chips (cons 'salty newlat))
L (add1 R))))
|
Step 8
new: salty
oldL: fish
oldR: chips
lat: ()
lat is null so we return the empty list and two 0’s to the last procedure we generated as the col:


🙂
evens-only*

|
1
2
3
4
5
6
7
8
9
10
11
12
13
|
(define evens-only*
(lambda (l)
(cond
((null? l) '())
((atom? (car l))
(cond
((even? (car l))
(cons (car l)
(evens-only* (cdr l))))
(else (evens-only* (cdr l)))))
(else (cons (evens-only* (car l))
(evens-only* (cdr l)))))))
|
Their version agreed.
evens-only*&co
See this stackoverflow thread for useful discussion of this procedure. In particular, see this answer and the flowcharts in this answer.
I’m just doing one “branch” or sublist (the (9 1 2 8)) but see the stackoverflow and especially the flow charts for full details. After I did the first branch I felt like I got the idea.

This is more or less what the book winds up eventually revealing as the answer:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
|
<br />(define evens-only*&co
(lambda (l col)
(cond
((null? l)
(col '() 1 0))
((atom? (car l))
(cond
((even? (car l))
(evens-only*&co (cdr l)
(lambda (newl p s)
(col (cons (car l) newl)
(* (car l) p) s))))
(else (evens-only*&co (cdr l)
(lambda (newl p s)
(col newl p (+ (car l) s)))))))
(else (evens-only*&co (car l)
(lambda (newl p s)
(evens-only*&co (cdr l)
(lambda (dnewl dp ds)
(col (cons newl dnewl)
(* p dp)
(+ s ds))))))))))
|

Initially, the l is ((9 1 2 8)( 3 10 ((9 9) 76 2).
col is the-last-friend.
l is not null and (car l) is not an atom, so we go to our final else clause and take the (car l) of the list l.
Branch 1
Step 1
l is ((9 1 2 8) 3 10 ((9 9) 7 6) 2)
col is the-last-friend.
the list is not null. (car l) is not an atom. We go to the final else line. Here is a detailed description of what happens there from stackoverflow. Where (car l) is a nested list:
Imagine you have the results from removing, summing and adding the numbers in
(car l)and call thesenewl,product, andsum; then imagine you have the results from doing the same thing to(cdr l), and call themdnewl,dproductanddsum. To your waiting continuation, give the values produced byconsingnewlanddnewl(since we’re producing a list of lists); multiplying togetherproductanddproduct; and addingsumanddsum.
So I’m going to break the col‘s up into named subprocedures again, using a flow chart from stackoverflow as a guide.
y1 partially represents what happens in the final else line of evens-only*&co:

|
1
2
3
4
5
6
7
|
(define y1
(lambda (al ap as)
(evens-only*&co '(3 10 ((9 9) 7 6) 2)
(lambda (dl dp ds)
(the-last-friend (cons al dl)(* ap dp)(+ as ds))
))))
|
To get the correct value for the overall final procedure, we can invoke y1 with ‘(2 8) 16 10, which represents the 1) list of even numbers, 2) product of evens, and 3) sum of the odds, for list (9 1 2 8). If we use these values, we get the right answer. The exact mechanism by which we calculated these numbers has not yet been revealed, and we’re just taking them as a given for now (I pulled them from the chart). The actual source of the numbers is invoking evens-only*&co on (car l), (car l) in this context being (9 1 2 8). So let’s analyze what the result of that would be so we get a better understanding as to what’s going on.

Step 2
l is (9 1 2 8)
col is y1
l is not null.
(car l) is an atom but not even.
So we analyze it under the else clause for when atoms are not even.
y2 partially represents what happens in that else clause:

|
1
2
3
4
|
(define y2
(lambda (newl p s)
(y1 newl p (+ 9 s))))
|
Note that, within the lambda, the 9 from l is already in the procedure. Where’s it coming from? It’s the car of l.
Note that the else clause invokes evens-only*&co* on (cdr l). We’ll keep recursively invoking that to get more values.
To get the correct final value for the overall procedure, can invokey2 with the list '(2 8) (the list of even numbers from l) as the first argument, the number 16 (the product of the even numbers from l) as the second argument, and 1 (the first odd number from l) as the third argument:

Step 3
l is (1 2 8)
col is y2
l is not null, and (car l) is an atom but not even, so this will be similar to before.

|
1
2
3
4
|
(define y3
(lambda (newl p s)
(y2 newl p (+ 1 s))))
|
The values that generate the correct final output when passed to y3 are ‘(2 8) 16 0:
![]()
Step 4
l is (2 8)
col is y3
l is not null and (car l) is even. From stackoverflow:
Imagine that you have the results of removing odd numbers, multiplying evens, and adding odd numbers from the
cdrof the list, and call themnewl,product, andsumrespectively.consthe head of the list ontonewl(since it’s an even number, it should go in the result); multiplyproductby the head of the list (since we’re calculating product of evens); leavesumalone; and pass these three values to your waiting continuationcol.

|
1
2
3
4
|
(define y4
(lambda (newl p s)
(y3 (cons 2 newl)(* 2 p) s)))
|
You can see that y4 is pulling the (car l) (or 2) in in a couple of places here – consing it onto newl and multiplying it by p. Once again, in the actual procedure, we’re getting our arguments to the lambda from the result of a recursive call, but we can also invoke y4 with those arguments, which are (8) 8 0
![]()
Step 5
l is (8)
col is y4
l is not null and (car l) is even.

|
1
2
3
4
|
(define y5
(lambda (newl p s)
(y4 (cons 8 newl) (* 8 p) s)))
|
To get the correct final values with y5, you invoke it with ‘() 1 0

Step 6
l is ()
col is y5
y5 is null. pass '() 1 0 to y5: