Category: Programming

Commandments

Selected Portions of Exercises

rember* (remove all instances of a value)

Wasn’t sure how they wanted the reader to go about this one so I peeked at the beginning of their answer:

Ok that makes sense so far. Next line is:

Ah of course. So maybe after we check if car l is an atom, if that turns out to be the case, we check if it’s eqan? to a?

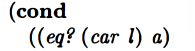
Ok they seem to want to use eq? even though eqan? seems more general. Ok so a is equal to car l, we call rember* with cdr l?

Looks good so far…
Ok then and if car l is not an atom, and we know l isn’t null, do we want to call rember* with car (car l) or something? Cuz we want to get inside these nested structures, right?
No. Just calling rember* with car l in the place of l is fine. That will let us “dig” into the nested structure.

But first, consider, what if car l is an atom but it’s not equal to a? Then we want to cons (car l) together with the result of calling rember* on the rest of l.

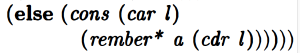
And then finally, if (car l) isn’t an atom, we want to call rember* both on the first element and on the rest:

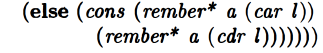
Oh and we want to cons the results of these calls because we want to make sure we capture the structure of the list.

The whole thing:

This is a big jump up in complexity from previous stuff.

insertR* (insert new word to right of every instance of old word)

We defined multiinsertR in a previous chapter, but that can’t handle nested list structures, which is what we’re working on in this chapter.

insertR* builds a lot on multiinsertR. The two new things we add are: 1) a check for whether the first element of a list, car lat is an atom before we check whether car lat is equal to old, and 2) an else to handle the situation where car lat isn’t an atom (in which case we cons together the result of calling insertR* on the first element of the list and the rest of the list, respectively):

Initially I had the second cond clause as ((atom? lat)). That was a mistake. That would lead to us “digging down” into the structured list until we hit an atom, at which point we’d be trying to invoke null? on an atom:

Initially I used lat for the name of the third argument, but we’re not necessarily dealing with a lat here! So I changed that.

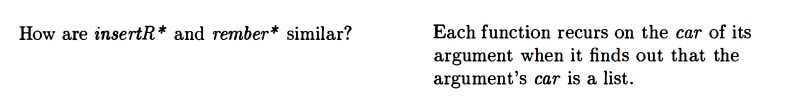
I think this is a reference to the final else in both procedures. If you know the argument’s car isn’t an atom, then you know it’s a list.

multirember doesn’t recur on the car cuz it’s assuming a “flat” list with no nesting, so it just needs to move “from left to right” within the list. It doesn’t need to “dig” or “burrow” into nested structures, which is what recurring on car does.

occur* (count occurrences in nested list)

Now they want something that counts the number of occurrences of something within a nested list structure:

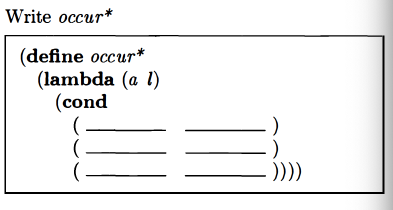
My answer, which matches theirs besides the name:

subst* (substitution within a nested list)

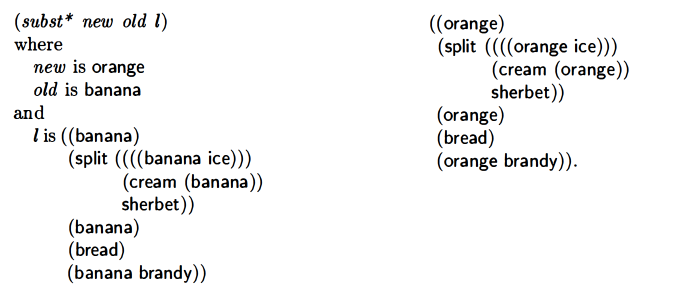
My answer:

This is essentially the same as theirs.

insertL*

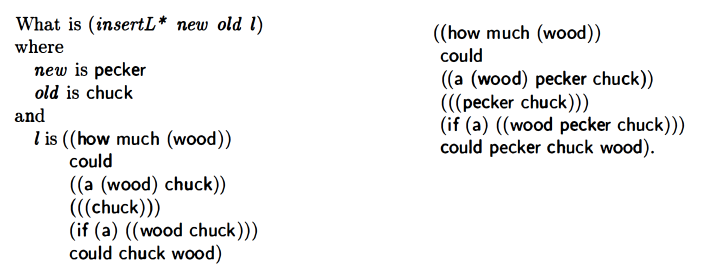
My attempt to write insertL*:

member*

This was the original member? function:

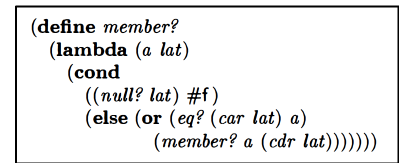
My attempt at writing member*:

They agree.

leftmost

My attempt at writing leftmost:

They agree.

eqlist?

eqlist checks if lists are equal:

Wasn’t sure how to write this one. Let’s take a peek.

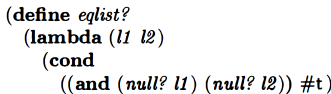
Ok. Pretty much what I expected so far. If both lists are null then we return true makes sense.

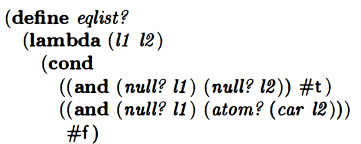
Didn’t expect this next line. Let’s think about it.
Oh, if the first list is null and the first element of the second list is an atom, return false. Makes sense. If you know that both lists aren’t empty, and that the first list is empty and the second list has an element, you know they’re not equal.

So by the time we’d get to this line in the procedure, we would know that it’s not the case that both lists are empty, and that it’s not simultaneously the case that the first list is empty and the second list has an atom as the first element.

So now we’re checking if the first list is empty and return false if it is. This handles the case where the first list is empty and the first element of the second list is itself a list.

Now I think I’m starting to understand this bit from the book:

The possibilities we’re going to have to deal with are:

L1: Empty. L2: Empty. (return true)

L1: Empty. car of L2: Atom. (return false)

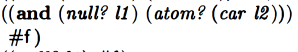
L1: Empty. car of l2 is a list. Return false.

The next one I guessed before checking:

car of L1: Atom. L2: Empty. Return false.

Guessed it correctly as you can see:

Ok so, i figured there would be a test involving eqan but didn’t really know or predict what shape it would take:

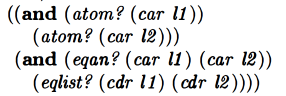
So we check that both car l1 and car l2 are atoms in the first part of the cond clause, and if that’s true, then we check that car l1 and car l2 are equal, and also make a recursive call to eqlist? with the rest of the lists. lots of stuff going on in this clause!

The next clause handles the case where car l1 is an atom and l2 is a list:

---

I think I’m starting to get the idea. Probably worth trying to think about all the possible cases we need to handle at this point. There are nine questions as the book says cuz there are two arguments and three possibilities for each.

• l1 & l2 are empty
• l1 is empty, (car l2) is an atom
• l1 is empty, (car l2) is a list
• (car l1) is an atom, l2 is empty
• (car l1) and (car l2) are atoms
• (car l1) is an atom, (car l2) is a list
• (car l1) is a list, and l2 is empty (this would be ((null? l2)).
• (car l1) is a list, and (car l2) is an atom (this would be ((atom? (car l2)))
• (car l1) is a list, and (car l2) is a list (would this be an else clause where you’d recur on both?)

And then let’s think about what we’d want to return in each of these cases:

• If l1 and l2 are empty, we want to return true because the lists being empty means we either got to the end of the lists without returning false (so the lists are the same), or both lists were empty from the start (and thus the same).
• If l1 is empty and (car l2) is an atom, that means the first list has reached an empty state while the second list still has an element. Since we should be proceeding through the lists at the same pace, element by element, if one list “runs out” of elements before the other one does, that indicates that the lists are not the same, and so we should return false.
• If l1 is empty and it is neither the case that either l2 is empty nor that (car l2) is an atom, then by process of elimination, (car l2) must be a list. Assuming our program proceeds through the lists correctly, if one list “runs out” of elements before the other one does, that indicates the lists are not the same, so we should return false in this case.
• If (car l1) is an atom and l2 is empty, then, for reasons previously stated, that indicates the lists are not the same, and so we should return false.
• If (car l1) is an atom and so is (car l2), then we want to check whether the actual values are the same. If they are then we recursively call eqlist with the remainder of the lists.
• If (car l1) is an atom and, by process of elimination, (car l2) is a list, then that indicates the lists are not the same and we return false.
• If , by process of elimination, we determine that(car l1) is a list, and we also determine that(car l2) is empty, that indicates that the lists are not the same, and so we should return false.
• If (car l1) is a list (by process of elimination) and (car l2) is an atom, that indicates the lists are not the same, and so we should return false.
• If (car l1) is a list and (car l2) is a list, we should recursively call eqlist on both those lists in order to determine whether they’re the same list. EDIT: I left out that you should recur on both the first element of the list and the rest of the list.

OK, while I had to read most of the procedure to do so, I seem to have figured out the principle of how the procedure works:

Hurrah!

Regarding ordering, the book makes the point that it’s okay to ask (atom? (car l2)) in the second question because by that point we know the second list can’t be empty. (If we tried to take car of an empty list we’d get an error.)

The first three cases are:
– If l1 and l2 are empty,
– If l1 is empty and (car l2) is an atom, and
– if l1 is empty, and (car l2) is a list

The first case is the one we return true for. In all other cases we’re considering where the first list is empty, we return false. So I think the answer to their question is yes.

I’m clearer on the point now. We want to return false for every case where the first list is null and the second list isn’t. If we already know that it’s not the case that the second list is empty, but that the first one is, then we know..

…will always return true because of the first list being empty. And we can return false when this is the case. And therefore between these questions…

…we can address the three cases.

My attempt:

Mine was close to theirs, but they also consolidated the ((atom? (car l1) #f) and ((atom? (car l2)) #f) lines and got rid of the separate ((null? l2) #f) line:

equal?

Book says to write equal?. Wasn’t sure how to proceed so i peeked:

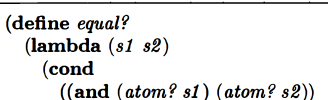
Ok that makes sense as a beginning. Let’s think about the cases:

S1: Atom: S2: Atom.
S1: list of s-expressions. S2: Atom.
S1: Atom. S2: List of s-expressions.
S1: List of s-expressions. S2: List of s-expressions.

If both s-expressions are atoms, we want to see if they’re the same somehow. Since they’re atoms, I don’t think we need to worry about checking for anything else in these case, since there’s no rest-of-a-list to check.

This is what I wrote:

And then I peeked at some more of the answer:

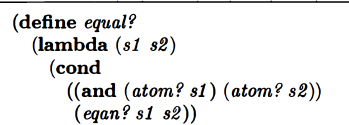
Ok looks good so far.
If you know that both arguments aren’t atoms, then you know that if one of them is an atom, the other one isn’t, so they aren’t the same. So then you should return false. My attempt at representing this before checking the answer:

And how they did it:

I think these are equivalent and so it’s fine. (EDIT: They ultimately simplified this)

If you know that neither of the two arguments is an atom, then they must be lists. We cannot compare lists directly, so we need to evaluate the lists further with a recursive call. My attempt at representing this before checking the answer:

Whoops. For some reason i was assuming we weren’t gonna use eqlist?, which we just made, lol. My approach actually produces an error, cuz my procedure can’t handle null?. Here’s the correct answer:

This is their simplified version, presented later:

rewriting eqlist?

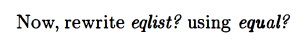
Hey this is kinda like mutual recursion.

So I did this:

I reasoned since equal? (or myequal?) can handle the cases where two arguments are both atoms or where one is and atom and one isn’t, we could cover all those by just testing to see if car of either l1 or l2 was an atom, and then invoke myequal if either one was true. I thought we should keep the null? tests and also keep the part that addresses the case where car of both lists are themselves lists. It looks like their procedure might be even simpler than this though so let’s see what they did:

So they kept the null? tests. But they dropped the part that checks if car of a list an atom and then invokes equal? if it is. Also, in the else clause, they make a call to equal? in the first part instead of eqlist. Let’s think about this.

If we know that neither list is empty, then we know that the first element in those lists must either be an atom or a list. equal? can deal with atoms and lists (the latter by calling eqlist). So really, given the existence of equal?, the main issue eqlist? needs to deal with is whether either list, or both of the lists, is/are null. Once eqlist? checks for that, and if that’s not the case, it can send the car of those lists to equal? to be dealt with. It also recursively calls itself with cdr of the lists. I think this makes sense.

simplifying rember

We want to keep the null? line. OTOH, since equal? can handle both atoms and lists, maybe we just need an else line?
If we know l isn’t null, we know car l is gonna grab something and not give an error. equal? can handle both atoms and lists. Whenever we find that s and l match, whether s is an atom or a list, we want to “remove” that from what we return by returning the rest of l. Otherwise, we want to cons (car l) together with a recursive call to remeber with the remainder of the list in order to maintain the recursive structure.

My attempt:

Their version is essentially the same except for the details of how they structured the cond clause (I think this is just a stylistic difference):

Oh gp yeah, it’s doing a different thing than it did before.
Oh they ultimately did further simplification:

This way of writing stuff is pretty intuitive now from my Simply Scheme work. I find Little Schemer’s way less intuitive. I think part of the reason is I know what the shorter version means and it’s also cleaner, so it seems more organized to me, while the Little Schemer version seems messy. Trying it the Little Schemer way has value though. I’ve been kind of going back and forth.