Simply Scheme Chapter 19 – Implementing Higher-Order Functions

My work on https://people.eecs.berkeley.edu/~bh/ssch19/implement-hof.html

This chapter is about writing higher-order procedures.

I compare my work to other people’s solutions some in order to gain perspective on different ways of solving some problems.

I am also consciously trying to “oversolve” procedures from different angles.

Chapter Notes

The chapter contrasts every and map:

The key difference is the use of cons, car, and cdr in map versus se, first, and butfirst in every.

map will preserve a structured list whereas every won’t, because every uses se to combine the elements of the result, wheres map uses cons:

Regarding accumulate, the book says you might expect to have to provide the combiner, the values to be combined, and the identity element in order to generalize the pattern involved in accumulate, but the book folks dropped the need for the identity element by simply returning the remaining element when you’re down to one element. Nice trick.

The book says how robust to make a program in terms of the program behaving politely when given incorrect input is a matter of judgment.

Exercises

✅ 19.1

What happens if you say the following?

The cdr procedure is applied to every element within the list, leading to the output '(lennon mccartney harrison starr).

How is this different from using map, and why?

With every the result is “flattened” into a sentence due to the use of sentence to join results in every. With map the sublists remain: '((lennon) (mccartney) (harrison) (starr)).

How about cadr instead of cdr?

every cadr has the same output as every cdr. To discuss one of the elements in detail, cdr of '(john lennon) is '(lennon) and cadr of '(john lennon) is 'lennon. You might thus expect the values returned by every cadr to vary from every cdr, but the results are combined internally in every using sentence and so the nested lists are flattened into a single “sentence” list that appears the same regardless of whether the Beatle names being dealt with are words or sentences.

OTOH, map cadr varies significantly from map cdr. Because map cadr deals with the Beatle names as words, there’s no nesting in the resulting list – the output is a single flat list that is the same as in the every examples.

✅ 19.2

My Solution 1 – No Combine

Write keep. Don’t forget that keep has to return a sentence if its second argument is a sentence, and a word if its second argument is a word.
(Hint: it might be useful to write a combine procedure that uses either word or sentence depending on the types of its arguments.)

My answer:

I did not write a combine procedure cuz it seemed unnecessary. Instead, I used an if within the consequent of the second cond clause.

I did make keep2 a “screener” procedure designed to check for a problematic case (when no input is provided for the second argument). If that check is passed, then the function and input are handed off to real-keep2.

I gave keep2 the following tests:

and I got the following outputs:

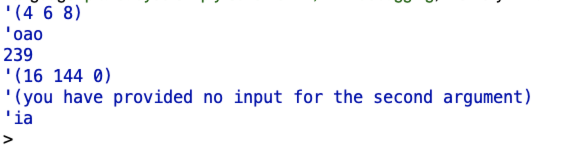
These outputs were as expected.

My Solution 2 – Combine

I then decided to try writing a version with combine.

We want to look at whether arg2 is a sentence within combine because, if a sentence is provided as the input, the second arg will always be a sentence, even if an empty one, whereas the first arg might be a word. See (keep3 even? '(3 4 5 6 7 8)) as an example:

real-keep2 worked differently because it checked whether the whole input to the procedure was a word?, instead of checking whether first input (the first element of the word or sentence) was a word.

The keep3 procedure managed to produce the desired output for the tests mentioned earlier.

buntine’s solution

Here’s buntine’s solution:

buntine actually made the combiner the thing that did the real work in his procedure, whereas I just used it to combine two arguments at a time.

buntine actually passes in a null-value to his combine, which is something I managed to avoid doing by returning the actual null value of the input when it became empty.

I looked at how keep was actually implemented in the scheme variant used in the book, but it was longer than I expected and had some stuff I did not understand.

✅ 19.3

Write the three-argument version of accumulate that we described.

My answer:

It produces the correct output for the three cases they give as examples above.

buntine used car and cdr instead of first and butfirst but his solution is essentially the same.

✅ 19.4

Our accumulate combines elements from right to left. That is,

computes 2−(3−(4−5)). Write left-accumulate, which will compute ((2−3)−4)−5 instead. (The result will be the same for an operation such as +, for which grouping order doesn’t matter, but will be different for -.)

for regular acccumulate the output we get using the above example is -2. For left-accumulate we expect -10.

for left-accumulateI started with Chapter 19’s version of accumulate but changed both the order of the arguments to the combiner and changed the selectors from first and butfirst to last and butlast:

I didn’t see any need to change the base case, as when you’re only down to one element it doesn’t matter whether you’re checking for the first or last element – it’s all the same.

Anyways those changes seemed to do the trick. This trace result and output is what I would expect if left-accumulate was working correctly:

You can see left-accumulate working its way down to the base case, returning 2, then performing (2 - 3) and returning -1, and so on, till we get the expected -10.

I tried another test:

And compare this with their accumuate procedure, which I gave a different name so that I could trace it:

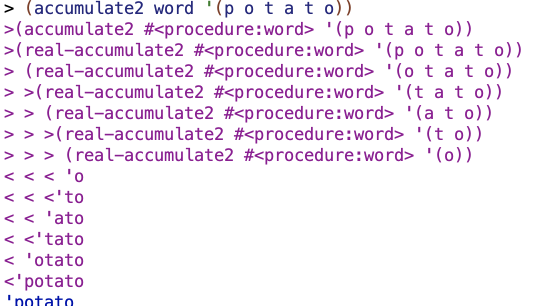
You can see that the procedures proceed through the same input in exactly the opposite manner.

My answer is almost the same as Meng Zhang’s, a guy with a Simply Scheme github repository I just discovered. He changed the base case selectors to butlast and last and didn’t import all the stuff from the book into his main left-accumulate procedure, but otherwise our solutions are very close.

✅ 19.5

Rewrite the true-for-all? procedure from Exercise 8.10. Do not use every, keep, or accumulate.

So my previous answer was:

And here’s an example of the desired behavior:

Looks pretty straightforward.

My answer:

I looked at a couple of other answers and mine seemed like the most elegant solution to me 😊

✅ 19.6

Write a procedure true-for-any-pair? that takes a predicate and a sentence as arguments. The predicate must accept two words as its arguments. Your procedure should return #t if the argument predicate will return true for any two adjacent words in the sentence:

Hmm this one’s interesting 🤔

My Solution

My answer:

I’m really getting a lot of mileage out of that trick they described in Chapter 19 re: accumulate, where you check if bf stuff is empty and then return the last element of the list. Here I extended that a bit, and did the list equivalent of checking if (bf (bf stuff)) was empty. That’s what cddr input is checking for, basically – it’s seeing if there’s a third element in the list. If not, cddr input will be empty, and so we can run the function fn on car input and cadr input (the first and second elements, respectively, that remain in our list) and get that result and wrap the procedure up.

However, if there is actually a third element, then we invoke or with a couple of arguments. We use or here because we want to know if any of the pairs return true for the procedure, whereas in the last problem we wanted to know if the elements were all true for the function, so we used and. Anyways, the first argument to the or is the function called with the first two elements of our list. The second argument is a recursive call to true-for-any-pair?. The arguments to that recursive call are of course fn and also cdr. We do cdr because we need to test each adjacent pair, so even though we might have already tested an element as the second argument to the function, we still need to test it as the first argument to the function.

My procedure assumes that the input sentence has at least two elements. If you give it a one element list or an empty list you will get an error:

The procedure will stop running as soon as it hits a true value:

Meng Zhang’s Solution

Meng Zhang also had an elegant solution:

His approach is slightly different. First, he uses a cond rather than an if. Also, his base case is a one element list. Therefore, his procedure can handle one element lists and only gives an error on the empty list. Furthermore, he explicitly returns true and false values. There are some other differences. Anyways, I thought it was pretty elegant.

✅ 19.7

Write a procedure true-for-all-pairs? that takes a predicate and a sentence as arguments. The predicate must accept two words as its arguments. Your procedure should return #t if the argument predicate will return true for every two adjacent words in the sentence:

So this problem was a gimme in light of my solution and discussion of 19.6. For 19.6 we used or because we wanted to return true if any pair was true. For 19.7 we want to return true only if all the pairs are true, so:

✅❌ 19.8

Technically solved this but didn’t really respect the spirit of how to use the helper function.

Rewrite true-for-all-pairs? (Exercise 19.7) using true-for-any-pair? (Exercise 19.6) as a helper procedure. Don’t use recursion in solving this problem (except for the recursion you’ve already used to write true-for-any-pair?). Hint: You’ll find the not procedure helpful.

Problem requirements:

1) use true-for-any-pair? as a helper procedure in true-for-all-pairs?
2) do not use recursion in true-for-all-pairs?

Cases that need to be addressed:

I) predicate fn is not true for all pairs
II) predicate fn is true for all pairs

Incomplete solution:

the case i addressed in my incomplete solution is only a subset of case I

if i had a true-for-some-but-not-all-pairs? procedure, i could do something like this

My Solution

This works but I don’t think it’s what they were looking for. However, it does meet the technical requirements of the problem:

Some explanation:
1. Within true-for-all-pairs?, (let ((secondlist (append (cdr input) '(())))) makes a second that consists of the cdr of the first list with an empty list appended. So if the first list was (a b c d e) then secondlist is (b c d e ()). The empty list is created so that both lists have the same number of elements, which is a requirement for map to be invoked on two lists.
2. (map make-pair input secondlist) returns a list from the the initial input list. This new list consists of a list of pairs from the input plus an empty value at the end. So for input '(a b c d e), this line generates ((a b)(b c)(c d)(d e)()). This is accomplished using the helper procedure make-pair.
3. remove-empty removes the empty list from the lists of lists now that we don’t need an empty list placeholder anymore.
4. (lambda (arg) (true-for-any-pair? fn arg) returns a procedure true-for-any-pair? with the given fn.
5. andmap applies the true-for-any-pair? from the lambda to each element in the list of lists we generated, and then “sums up” the resulting truth values from those invocations of true-for-any-pair? by applying the logical operator and to them.
The reason I say I don’t think this is what the book was looking for is we’re not really using true-for-any-pair? in any important way here. we could take this approach to solving true-for-all-pairs? without needing to use true-for-any-pair?. Also we didn’t use not in our main procedure.

Meng Zhang’s Solution

With Zhang’s solution you check whether each pair is NOT true for the predicate. if it’s the case that any pair is NOT true, then true-for-any-pair? would return false, but for the opening not. but then he has the NOT around the whole true-for-any-pair? procedure. so the logic is, if it’s NOT the case that the predicate is NOT true for any pair, that’s the same as saying that the predicate is true for all pairs, so we return true.

✅ 19.9

Rewrite either of the sort procedures from Chapter 15 to take two arguments, a list and a predicate. It should sort the elements of that list according to the given predicate:

Explanation of Sort

Ok. Here’s the original sort procedure from chapter 15 with its supporting helper procedures:

To recap (and since I didn’t do detailed analysis on this procedure before in Chapter 15 and its coming up again): the purpose of this procedure is to sort words in a sentence alphabetically. This procedure works by the following method: sort first looks for the earliest-word in the sentence.

The real action as far as finding the earliest word occurs in earliest-helper. earliest-helper takes two arguments: the first word of the sentence (so-far) and the remaining words in the sentence (rest). If we “run out” of rest words in earlier helper – that is, if rest becomes empty? – then we know that so-far is in fact the earliest word and we return that.

While we still have words remaining in rest, we check – and this is the really key part for my solution to this problem – whether so-far is before? the first value of rest. before? is a Scheme primitive. So basically we’re checking if the current candidate (so-far) for the earliest word in the sentence comes before the first sentence of the remaining candidates for the earliest word in the sentence – (first rest). If so-far does indeed come before (first rest), then so-far retains its status as the current candidate for earliest word in the sentence, and this is reflected in the resulting recursive call we make – (earliest-helper so-far (bf rest))). We keep so-far the same and decide to check it against the next potential candidate. OTOH, if so-far does not come before (first rest), we move to the else line, which replaces so-far with (first rest) as the new so-far.

Jumping back to the sort procedure, sort joins the result of (earliest-word sent) together in a sentence with a recursive call to itself, but the particular argument used is interesting. sorttakes a sentence as an argument. sort recursively calls itself with the first instance of the earliest word in the sentence removed from the sentence. In this way, the earliest word can be found.

My Solution (Editing Sort)

So my procedure in solving this problem was pretty straightforward. I decided that before? was the critical thing that made this procedure an “alphabetical sorter”. If we wanted to generalize the functionality, we’d need to get our function into the earliest-helper procedure so that it could replace before?. So I made the necessary adjustments to the arguments (and changed the name to sort2) and did just that:

With these adjustments, the procedure produced the desired output. We’ve generalized a sorting procedure! 🙂

My Solution (Editing Mergesort)

The same basic method — adding a fn argument and passing that down the chain of procedures to replace before? – worked for editing mergesort:

❌ 19.10

Write tree-map, analogous to our deep-map, but for trees, using the datum and children selectors.

This problem is really underspecified IMHO. They should have at least given an example desired output like they do with lots of problems.

Here’s what they said about deep-map:

This procedure converts every word in a structured list to Pig Latin. Suppose we have a structure full of numbers and we want to compute all of their squares. We could write a specific procedure deep-square, but instead, we’ll write a higher-order procedure:

They want a tree-map. Here’s what I find confusing … deep-map can navigate a tree, I think? Like datum just takes the car of something and children just takes the cdr of something. Is this just about trying to get us to respect the data abstraction like they talked about in Chapter 18?

This was my attempt, which seemed kinda lame to me but I couldn’t figure out exactly why:

This seemed to work. For example, I could run pass a plural function in and get the country names in the world-tree pluralized. But I was still feeling a bit stuck about what they were even asking for, so I decided to look at some other people’s answers.

Here’s Andrew Buntine’s:

This solution uses mutual recursion. It also makes use of make-node.

When I tried to use plural on the world-tree with this solution, I got an error:

✅ 19.11

Write repeated. (This is a hard exercise!)

First Attempt (failed)

repeated was described way back in chapter 8:

Here are some relatively straightforward examples of how it works:

I’ll name my procedure repeated2.

First I’ll try doing what I want to accomplish in the interactions window. Here’s what I imagine I want my procedure to do for ((repeated2 square 2) 3) (meaning: square 3 a total of two times):

Here was my first attempt:

For one copy of a procedure, it works fine:

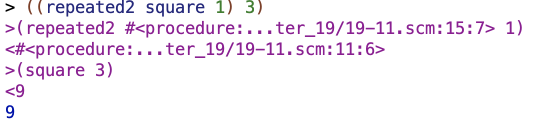
But for two there’s a problem:

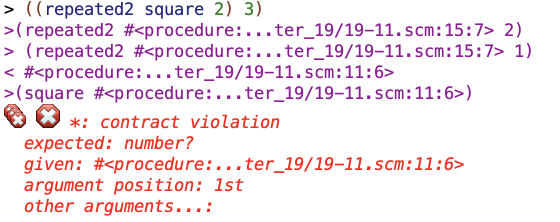
It looks like a procedure is being passed to the procedure I’m using as the fn in this example, square, instead of a number being passed to it. Why would that be happening? And why would it only be happening on the recursive call?

What I imagined happening in my mind was that repeated2 would arrive at the base case and then that base case lambda would “grab” the input value (in this example, “3”), run the square procedure, and then percolate the calculation on up through the chain of recursive calls before arriving at an answer.

I think what is actually happening is that the base case lambda doesn’t “grab” anything. Instead, it gets evaluated as being a procedure, and then that procedure gets fed in as the arg for the lambda one “step” up in the recursive chain, and then square tries to evaluate that procedure, and then goes “wtf this is not a number! it is a procedure.”

So that’s why this failed.

Second Attempt (success!)

I borrowed some code from my solution to Exercise 9.13 in chapter 9:

If the number of copies desired is greater than 1, repeated2 invokes compose with fn as the first function and the second function as the result of recursively calling repeated2 with 1 less than the current number of copies. So we build up a chain of compose fn (compose fn ... until ultimately arriving at one copy, in which case we just invoke the fn on an argument. So for something like ((repeated2 square 3)2) we get…

When the base case of 1 copy is arrived at, lambda procedure gets evaluated and a procedure that applies a function fn to an argument arg is returned. This unnamed lambda procedure gets composed by the compose closest to the base case, and compose is, after all, looking for a procedure g that takes an argument arg to compose with f. And then we have a procedure (fn (fn arg)) serving as g to an instance of compose “further up” the recursive tree, which in turn gets composed with fn once again. And since compose returns a procedure, this last instance actually gets returned and can be applied to the value we want to work on.

So, step by step, when the lambda in the base case gets evaluated, we have a procedure that applies a function to an argument.

This function gets passed as the g to compose, which is a higher-order procedure, and which outputs another function, which takes a function of a function applied to an argument. With the example we are consider, this procedure takes the square of the square of an argument.

When we get to 3 copies of the procedure, we have the following:

This, I think, is what the recursive invocations of compose resolve into once the base case is reached and the evaluations begin. And I can see why it works … like the syntax makes sense. In my first attempted solution, the way I structured the procedure was such that I was providing one procedure another procedure as an argument when it expected a value (like a number). But here, we don’t have that. Things are getting the arguments they expect to get.

❌ 19.12

Write tree-reduce. You may assume that the combiner argument can be invoked with no arguments.

I tried this but it’s pretty limited and requires manually specifying identities:

I tried looking at buntine’s solution:

It seems to work. What’s going on here?

If the tree is null, tree-reduce returns false. Otherwise it invokes the function on the datum of the tree and then invokes tree-reduce-in-forest on the children of the tree.

tree-reduce-in-forest just calls the func if the tree is null. I think this addresses the issue I was having with wanting to return the identity. A bunch of procedures return the identity if you invoke them with nothing:

Anyways, if the tree isn’t null, the procedure invokes the argument function on the result of calling tree-reduce with the car of tree and tree-reduce-inforest with the cdr. This is mutual recursion.

I also checked out Meng Zhang’s solution:

I intuitively like this one a bit better.
So if the tree is a leaf, we just return the datum of the tree. Otherwise we invoke the combiner argument function (such as +) on the result of getting the (datum tree) and the value returned by the forest-reduce procedure invoked with the children of tree. We see another mutual recursion pattern here.

Within forest-reduce, if the cdr forest is null (in other words, if the node being examined represents a leaf) then the car of the node is passed back to tree-reduce, where the datum will ultimately be returned. Otherwise, we invoke the combiner on the result of calling tree-reduce with the car of the node and forest-reduce with the cdr.

✅ 19.13

Write deep-reduce, similar to tree-reduce, but for structured lists:

My Solution

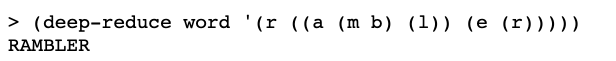
I figured out a couple of variants that seemed to work on the test input the book gives.

First, I imported some procedures from The Little Schemer:

Here’s my first variant procedure that seems to work:

And here’s the second:

Both variants return the lst when it’s an atom, apply the function fn to the list when it’s a list of atoms, and otherwise dig deeper into the function while invoking the fn on the results of that digging.

Other Solutions

I compared my answer to some others.

Here’s Meng Zhang’s:

I wonder about testing for word? here, since that kind of hardcodes what data type you’re looking for.

You can see that all the real action happens in the real-deep-reduce procedure. Also his deep-reduce is kind of a mirror of my deep-reduce-helper – both check if the structure is empty, and return the identity of the combining function if it is.

Here’s Andrew Buntine’s:

I’d wondered if it was possible to do everything in one procedure.
So Andrew’s solution uses the calling-the-function-to-return-the-identity-element trick in the null check.
Then if the first element is a list, it calls deep-reduce on both the car and the cdr of the list.
Otherwise, it applies the function to the car of the list and calls deep-reduce on the cdr.
I found this procedure easy to follow in terms of figuring out what was going on.