Simply Scheme Chapter 18 – Trees

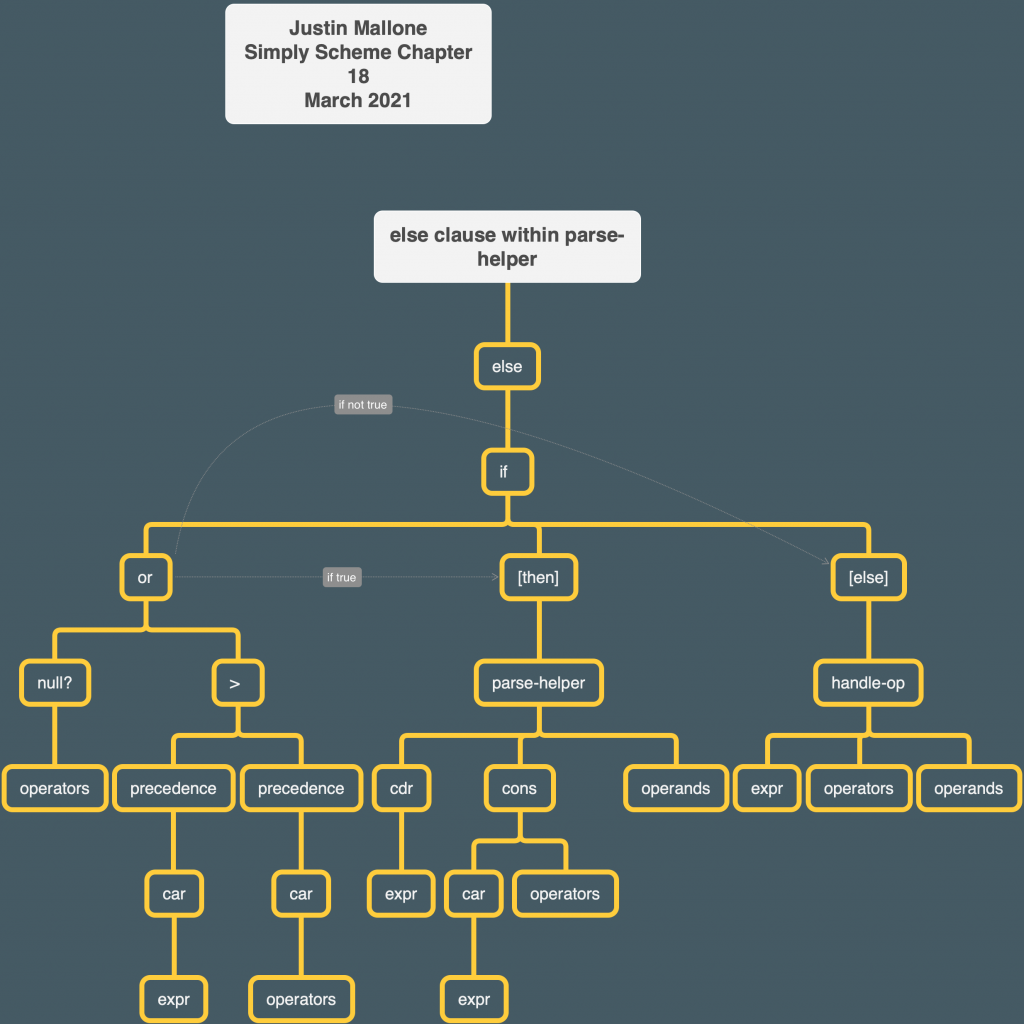
My work on https://people.eecs.berkeley.edu/~bh/ssch18/trees.html

This is more of a quote-and-commentary-heavy chapter for me as there are relatively few problems. The headings don’t necessarily correspond to sections within the chapter.

Trees

The big advantage of full-featured lists over sentences is their ability to represent structure in our data by means of sublists. In this chapter we’ll look at examples in which we use lists and sublists to represent two-dimensional information structures. The kinds of structures we’ll consider are called trees because they resemble trees in nature:

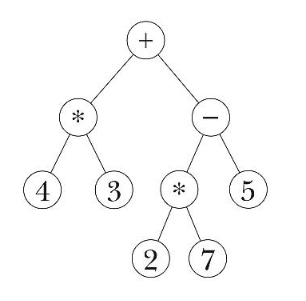
The components of a tree are called nodes. At the top is the root node of the tree; in the interior of the diagram there are branch nodes; at the bottom are the leaf nodes, from which no further branches extend.

[…]

We say that every node has a datum and zero or more children. For the moment, let’s just say that the datum can be either a word or a sentence. The children, if any, are themselves trees. Notice that this definition is recursive-a tree is made up of trees. (What’s the base case?)

Base case would be a node with no children, I think.

This family metaphor is also part of the terminology of trees.[1] We say that a node is the parent of another node, or that two nodes are siblings.

Mutual Recursion

The book presents this procedure:

And then proceeds to offer an alternative:

In Chapter 14 we wrote recursive procedures that were equivalent to using higher-order functions. Let’s do the same for count-leaves.

Note that count-leaves calls count-leaves-in-forest, and count-leaves-in-forest calls count-leaves. This pattern is called mutual recursion.

In this example of mutual recursion, count-leaves is the program that actually checks whether a specific element of the tree is a leaf, and returns the “1” value if so. If not, it then invokes count-leaves-in-forest to return the list of any children. count-leaves-in-forest returns 0 for a forest that returns null – that is, if the forest is empty (there are no children). Otherwise it adds the sum of count-leaves invoked with argument car forest and count-leaves-in-forest invoked with argument cdr forest.

Short summary: count-leaves-in-forest navigates through the tree list with car and cdr and count-leaves returns the 1 for actual leaves and invokes count-leaves-in-forest for non-leaves.

Mutual recursion is often a useful technique for dealing with trees. In the typical recursion we’ve seen before this chapter, we’ve moved sequentially through a list or sentence, with each recursive call taking us one step to the right. In the following paragraphs we present three different models to help you think about how the shape of a tree gives rise to a mutual recursion.

In the first model, we’re going to think of count-leaves as an initialization procedure, and count-leaves-in-forest as its helper procedure. Suppose we want to count the leaves of a tree. Unless the argument is a very shallow[2] tree, this will involve counting the leaves of all of the children of that tree. What we want is a straightforward sequential recursion over the list of children. But we’re given the wrong argument: the tree itself, not its list of children. So we need an initialization procedure, count-leaves, whose job is to extract the list of children and invoke a helper procedure, count-leaves-in-forest, with that list as argument.

Ah, so the invocation of the children procedure causes count-leaves to be the initialization procedure in this model.

The helper procedure follows the usual sequential list pattern: Do something to the car of the list, and recursively handle the cdr of the list. Now, what do we have to do to the car? In the usual sequential recursion, the car of the list is something simple, such as a word. What’s special about trees is that here the car is itself a tree, just like the entire data structure we started with.

To concretize, in the lengthy world-tree example they use in the chapter, world-tree is a tree with many children, but car (children world-tree) is likewise a tree with children.

Here’s world-tree:

And here are procedures operating on world-tree

Therefore, we must invoke a procedure whose domain is trees: count-leaves.

That makes sense.

This model is built on two ideas. One is the idea of the domain of a function; the reason we need two procedures is that we need one that takes a tree as its argument and one that takes a list of trees as its argument.

A tree includes its own datum plus the list of children. So we need one procedure for handling the whole tree structure and one procedure for handling just the list of children.

The other idea is the leap of faith; we assume that the invocation of count-leaves within count-leaves-in-forest will correctly handle each child without tracing the exact sequence of events.

The second model is easier to state but less rigorous. Because of the two-dimensional nature of trees, in order to visit every node we have to be able to move in two different directions. From a given node we have to be able to move down to its children, but from each child we must be able to move across to its next sibling.
The job of count-leaves-in-forest is to move from left to right through a list of children. (It does this using the more familiar kind of recursion, in which it invokes itself directly.) The downward motion happens in count-leaves, which moves down one level by invoking children. How does the program move down more than one level? At each level, count-leaves is invoked recursively from count-leaves-in-forest.

This model is the one that most easily fits my existing thinking/intuitions. I often like to think of what programs do in somewhat mechanical terms like “moving through” some set of data.

The third model is also based on the two-dimensional nature of trees. Imagine for a moment that each node in the tree has at most one child. In that case, count-leaves could move from the root down to the single leaf with a structure very similar to the actual procedure, but carrying out a sequential recursion:

The trouble with this, of course, is that at each downward step there isn’t a single “next” node. Instead of a single path from the root to the leaf, there are multiple paths from the root to many leaves. To make our idea of downward motion through sequential recursion work in a real tree, at each level we must “clone” count-leaves as many times as there are children. Count-leaves-in-forest is the factory that manufactures the clones. It hires one count-leaves little person for each child and accumulates their results.

And in the earlier version of count-leaves that used (reduce + (map count-leaves (children tree))))), it was the map function that was the factory which manufactured the clones.

Dealing with Trees

The following procedure figures out whether a datum is in a tree:

But the book describes it as inefficient, because it performs unnecessary computations even after it find the place being looked for. So they propose this rewrite:

More mutual recursion. in-tree? has the domain of trees, and in-forest? has the domain of a list of trees.

The or structure in in-tree? means that in-tree? will return true either if datum tree is equal? to place or if place is somewhere else in the forest.

Although any mutual recursion is a little tricky to read, the structure of this program does fit the way we’d describe the algorithm in English. A place is in a tree if one of two conditions holds: the place is the datum at the root of the tree, or the place is (recursively) in one of the child trees of this tree. That’s what in-tree? says. As for in-forest?, it says that a place is in one of a group of trees if the place is in the first tree, or if it’s in one of the remaining trees.

The next thing the book wants to be able to do is locate:

This is more complex than in-tree? because we want to say where a value is, not just say whether it exists somewhere.

The algorithm is recursive: To look for Berkeley within the world, we need to be able to look for Berkeley within any subtree. The world node has several children (countries). Locate recursively asks each of those children to find a path to Berkeley. All but one of the children return #f, because they can’t find Berkeley within their territory. But the (united states) node returns

To make a complete path, we just prepend the name of the current node, world, to this path. What happens when locate tries to look for Berkeley in Australia? Since all of Australia’s children return #f, there is no path to Berkeley from Australia, so locate returns #f.

locate first checks if the city is equal to the datum of tree. If so, it calls list on city (this makes sense later). Otherwise, it defines a let called subpath using locate-in-forest and the arguments city and children tree. subpath will only return true if a valid subpath exists. If it does, cons will create a list from datum tree and subpath.

If a subpath doesn’t exist, the procedure will return false.

Let’s walk through this procedure looking for ‘berkeley in the world-tree. I’m truncating the output of trace here cuz it’s quite long. First locate checks if berkeley is equal to world.

It isn’t, so then locate-in-forest runs with berkeley.

The procedures try to find Berkeley in Italy first, since that’s the first country in the world-tree, but do not meet with success.

Then the procedures get to the US. First locate checks whether the united states is equal to berkeley. This is not the case.

The procedures start to drill down and ultimately find a match

I wanted a more detailed view of what was going on in this procedure, and in particular how the stuff got appended together.

I discovered Scheme’s begin procedure. The utility of begin for debugging is described here.

Here’s my reworked locate:

So locate arrives at berkeley. Since city is equal to (datum tree), we run list city, returning '(berkeley).

Now, for the call (locate 'berkeley '(california (berkeley) ((san francisco)) (gilroy))), we know what the subpath is – (berkeley). So we cons california with '(berkeley).


This general pattern repeats as we percolate back up the tree of calls

using (list (datum tree) subpath)) would not get us the output we want, btw:

Abstract Data Types

These procedures:

define an abstract data type for trees, wherein “a tree is a list whose first element is the datum and whose remaining elements are subtrees.”

The book notes that you can deal with nodes by using car and cdr but using the ADT-specific selectors helps program readability. This is a good point – you should use your abstractions, not fight them by using lower-level stuff.

Getting Unstuck 🤔

Having some trouble with this chapter. This section reflects my efforts at getting unstuck:

Domain, range, and purpose of procedures dealing with treees and world-tree

General tree procedures

make-node

• domain: a word or list as the first argument and a list as the second argument. (You can give make-node a word as the second argument but then you will get the “dot” output described in an earlier chapter.)
• range: a list whose car is the first argument and whose cdr is the second argument.
• intended use within Tree abstract data type: combine a word or list representing the name of a place (e.g. 'world, '(united states)) with a list of children of the place. If there is a higher level entity above the level of entity upon which make-node is being invoked, the invocations of make-node should be enclosed in an invocation of list, as in the following example:
  

  

datum

• domain: a list
• range: the car of that list, which may be a word or a list
• intended use within Tree abstract data type: get the first element of a list, representing the “label” of a particular node.
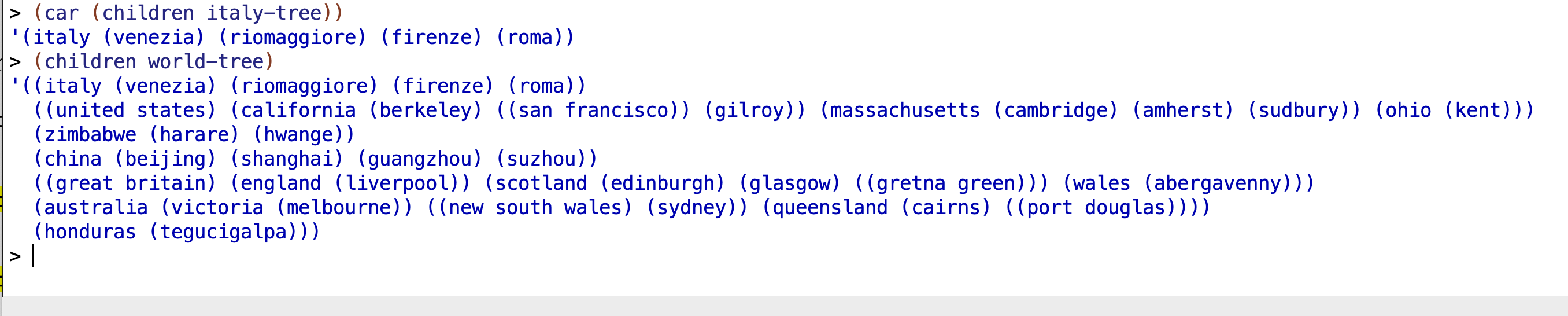
• Note that nodes return within nested lists when using the children procedure, so you need to do datum (car (children tree))) to get the datum of a child tree. For example, consider the italy-tree I made:

If we want to return “italy”, we need to do (datum (car (children italy-tree))):

If we just do (datum (children italy-tree)), which is what I tried initially, this happens:

This is because the entirety of (italy (venezia) (riomaggiore) (firenze) (roma)) returns within a nested list when children is invoked on italy-tree (keep in mind that 'world was the root node within italy-tree):

If we want to be able to get at just 'italy by itself, we need to invoke car on this nested list so we can get the list that datum can address:

children

• domain: takes a list with more than one element as an argument
• range: returns the cdr of the list as a list
• intended use within Tree abstract data type: return the children of a given node.
• Example:
  

world-tree specific procedures

cities

• domain: a list.
• range: a list containing the elements of the list provided as an argument to the procedure.
• intended use within world-tree: takes the leaf procedure and applies it to a list containing the names of cities, which, in the context of the world-tree, will always be the leaves. This is a bit neater than having to apply make-node on a bunch of individual cities and then group them together in a list.

leaf

• domain: words, lists, numbers, booleans
• range: a list with the argument provided as the only element within that list.
• intended use within world-tree: the procedure invokes make-node with the argument provided to leaf as the first argument and with an empty list as the second argument (which represents the children within make-node). This creates a list with no children, or a leaf. Thus this procedure is designed to create nodes with no children.

Analyze the procedures involved in the infix expression parser in detail

parse is initially invoked with the expression you are trying to parse.

This initializing procedure calls parse-helper with the initial expression and two empty lists representing the operators (meaning the arithmetic operators) and operands (meaning the numbers) respectively.

Within the first cond of parse-helper, we check whether the expr is null? in the predicate. If so, we evaluate a somewhat complex consequent which has an if statement. If the operators expression (the second argument passed into parse-helper) is also null?, we return the car of the operands list. Otherwise (meaning, if at least one operator remains) we pass an empty list representing the empty expression along with the operators and operands to handle-op.

If the first value of car expr is a number, we recursively call parse-helper with the cdr of expr, the current list of operators, and a longer expression. The longer expression consists of the cons of the following two expressions:
1. the result of invoking make-node with car expr and an empty list, which creates a node (in our tree abstract data type, which is represented by a list in Scheme) with the first number of the expr as the root, and
2. the existing operands list

I believe the process described in this cond is reflected in the following image – the procedure detects a number as the leading value of the expr and then adds that number to the operands list as a node/list:

The next cond clause checks if the car of expr is a list. This is necessary because we can have nested parenthetical expressions within our infix expression. If car expr is a list, then we recursively call parse-helper with cdr expr, operators, and a longer expression. The longer expression consists of the cons of:
1. the result of a call to parse with car expr as the argument, and
2. the list of operands.

The call to parse is to break down our sublist into a form we can use. It’s worth keeping in mind that the “operands” list is essentially also the “fully processed tree” list. We keep operations and operands list temporarily in order to deal with the issue of sometimes needing to wait until an expression is definitely “finished” before processing it, but ultimately the parse program is trying to construct a complete tree, with operators and operands, in the “operands” list. That’s why we’re only cons‘ing the results of the call to parse with operands and why that’s fine – because after the call to parse is finished with the sublist, we want the result of that internal processing in operands.

The else clause is the most complicated part of parse-helper.

I’m going to briefly describe precedence since it’s relevant:

If the operator passed into precedence appears in the list '(+ -), then return 1. Otherwise, return 2.

Back to the else clause. If either one of two conditions is met, we recursively call parse-helper with cdr expr, the cons of car expr and operators, and operands, respectively, as the arguments.

What are the two conditions?
1. If operators is null?, or
2. If the precedence of car expr is higher than that of car operators.

The second condition represents the case where the next expression in a list has higher precedence than the previous expression, as seen in the book example here:

Infix has implicit grouping based on the operation being performed (cuz of the Order of Operations).
When one operator has lower precedence than another one, that’s an indicator that the previous operation reflects a “complete” substatement. For example:

(4 * 3 + 2)
When we get to the +, we can be confident that the 4 * 3 represents a completed statement. Why? Because * represents an implicit grouping. With the above example the grouping is:

((4 * 3) + 2).

So in that context, the + becomes a bit like a close-parentheses indicator. If you had another operator of the same precedent, it wouldn’t be a close-parentheses indicator. E.g.:
(4 * 3 / 2)
The above expression has no implied hierarchy of precedence that you need to translate the expression into by adding parentheses – you should perform the operations from left to right, cuz * and / have the same precedence.

All that said, because * is higher precedence and not lower precedence than +, we have to add it to the list of operators.

So that takes care of the part of else that deals with precedence. What about the part that deals with when operators is null??

So keep in mind the previous cond clauses dealt with the cases where:
1. expr was null
2. car expr was a number
3. car expr was a list.

If we assume that infix expressions will consist of nothing but numbers, operators, and numbers, and we know that 1) expr isn’t empty, 2) car expr isn’t a number or list, then the first value in expr must be an operator.
The purpose of our whole parse program is to put infix expressions into a structured tree. To do that, we need at least two operands (numbers) and an operator. If we know that there are more values remaining in expr, and that car expr isn’t a number or list, and that operands is empty, then we know that we need to grab that first value from expr and add it to operators.

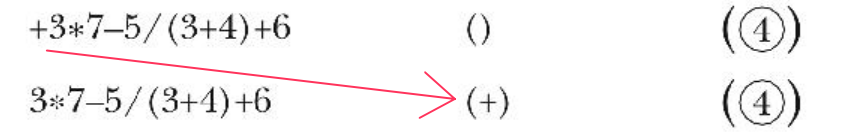
If, on the other hand, and given that the previous cond clauses have not evaluated to true, we know that 1) the operators list has an entry, and 2) the precedence of car expr is not higher than that of car operators, then we know we need to “handle” the car operators operator and put it in a tree:

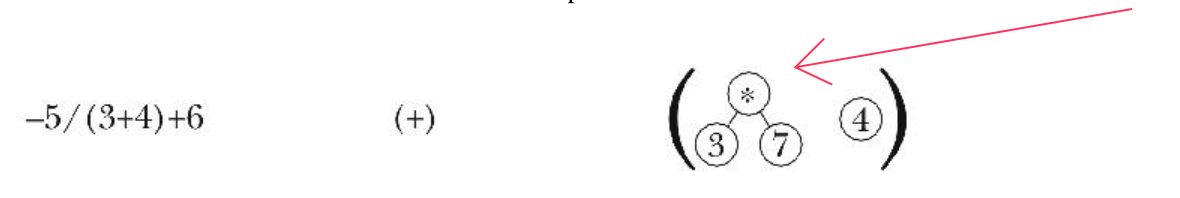
How does handle-op work?

handle-op calls parse-helper with expr as its first argument, the cdr of operators as its second argument, and a rather long argument as its third argument. This third argument consists of the cons of:
1. the result of calling make-node with car operators as the first argument and list (cadr operands) (car operands) as the second argument. This creates a tree structure with the first element of operators as the root of the tree, the second value of operands as the first element within the child of that tree, and the first element of operands as the second element within the child of that tree.
2. the cddr of the operands (representing the third element onward, the first two elements already having been assigned roles within the structure of a tree in the previous step)

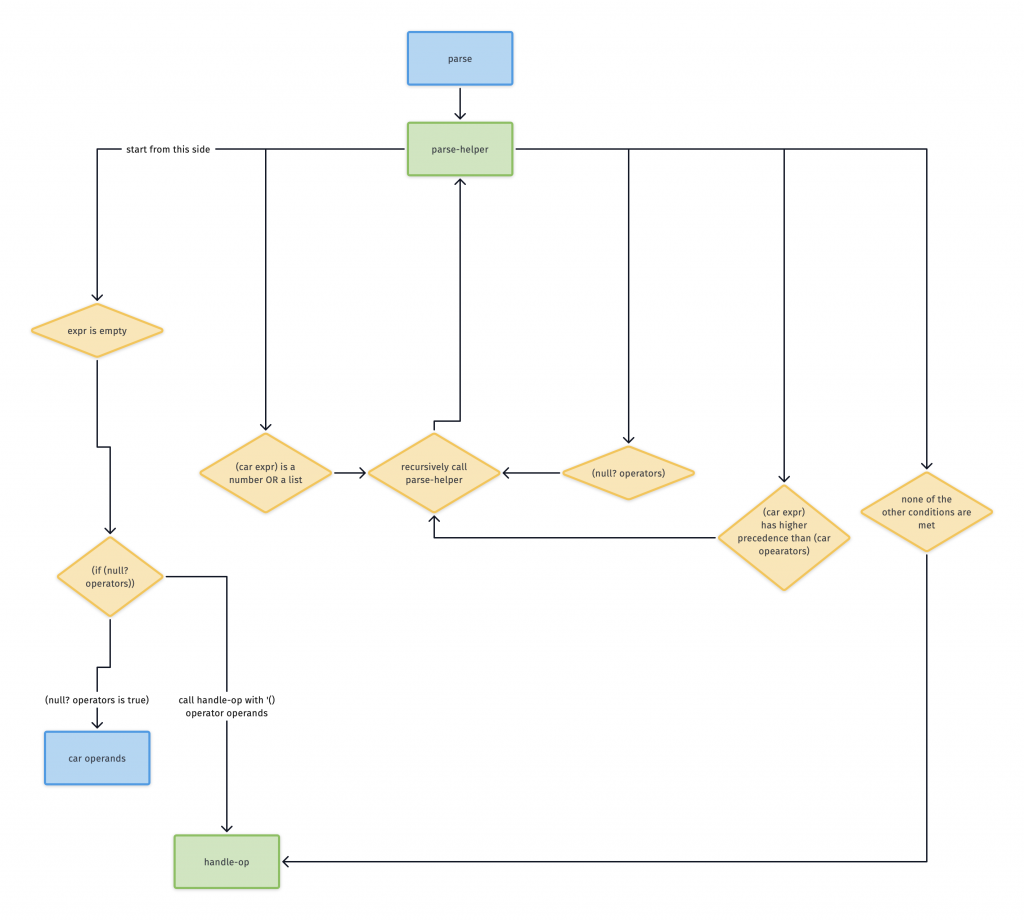
This diagram illustrates the general flow of parse-helper. The main point is to show how many recursive calls there are.

Exercises

✅ 18.1

What does
((SAN FRANCISCO))
mean in the printout of world-tree? Why two sets of parentheses?

I think one set of parentheses is to group the two words of “san francisco” together.
I think another set of parentheses is to indicate that “san francisco” is a node within the world tree.
All nodes have a set of parentheses around them, to indicate that they are nodes within our tree abstract data type. See Great Britain for example:

There are obviously the inner parentheses, but the first paren on the left is a “node” parentheses, which corresponds to the parentheses on the far right which I’ve highlighted. If Great Britain were a leaf node, these parentheses would be all that there was on the line besides the datum of Great Britain itself, and so it’d just be ((great britain)). Because Great Britain has children, however, the two sets of parentheses are a bit harder to see.
This is not the case with ((san francisco)), which is a leaf node, and thus has the two sets of parentheses right around it.

✅ 18.2

Suppose we change the definition of the tree constructor so that it uses list instead of cons:

How do we have to change the selectors so that everything still works?

When I tried to run locate 'berkeley world-tree after this change, it failed:

After making the following change to children, locate worked properly:

Likewise, count-leaves failed initially after making the change to make-node but worked after making the change to children above.

I also tried stuff like this:

It failed after making the change to make-node but succeeded after making my change to children.

I checked my answer against buntine’s answer:

Answer: If we used list instead of cons then we would have a list that two elements; a word and a list.
Cons: '(australia (wa (perth)) (nsw))
List: '(australia ((wa ((perth))) (nsw)))
For things to still work, we’d need to use cadr, or perhaps (datum (children x)).

I found this a bit unclear. It doesn’t say what specific selector you should use cadr for. Although since I did use cadr in my change to children, it is at least potentially compatible with mine.

I also checked this page but the changes suggested did not seem to work.

❌ 18.3

Write depth, a procedure that takes a tree as argument and returns the largest number of nodes connected through parent-child links. That is, a leaf node has depth 1; a tree in which all the children of the root node are leaves has depth 2. Our world tree has depth 4 (because the longest path from the root to a leaf is, for example, world, country, state, city).

I was stuck on this one for quite a while. I finally gave up and looked at buntine’s solution. He said this one took him forever so I don’t feel so bad!

Alright so he uses mutual recursion.

First, in depth, he checks if a tree is a leaf. If so he returns 1. If not he calls find-depth with the entire tree and 1. The arguments passed to find-depth indicate to me that depth is just an “initializer” procedure and find-depth is going to be part of a pair of recursive procedures.

Within find-depth, the current depth d is cons‘ed together with a call to find-depth-in-forest with the arguments children tree and (+ 1 d). The values returned from this are passed in as arguments to max using apply.

For find-depth-in-forest, we return the empty list if the tree is null. Otherwise, we cons together a call to find-depth with car tree as first argument and find-depth-in-forest with cdr tree as the first argument. For both these arguments, d is the second argument. Therefore, the d only gets incremented once in find-depth. I think this makes sense according to the models described in the chapter because find-depth is the procedure traveling “vertically” within the tree.

✅ 18.4

Write count-nodes, a procedure that takes a tree as argument and returns the total number of nodes in the tree. (Earlier we counted the number of leaf nodes.)

For reference, the world-tree has 44 nodes.

I started with the count-leaves procedure as a model:

My thinking was that basically we want to do count-leaves but a bit more. In other words, we want to count the leaves but also something else.

In coming up with my solution, I initially started trying to work with the world-tree but ultimately decided that was too big. I made a smaller italy-tree of my own to play around with, just to test my solutions with a smaller set of data.

I came up with this as my answer:

This is extremely similar to count-leaves. We are still counting all the leaves, which remain the base case. The difference now is that for each non-leaf, we are adding a 1. This simple change causes us to count all the nodes instead of just the leaf nodes.

buntine solved this with mutual recursion rather than using map. You can see that is main procedure is very similar to mine.

✅ 18.5

Write prune, a procedure that takes a tree as argument and returns a copy of the tree, but with all the leaf nodes of the original tree removed. (If the argument to prune is a one-node tree, in which the root node has no children, then prune should return #f because the result of removing the root node wouldn’t be a tree.)

My answer:

I made not-null? to help with using filter.

To comply with the desired output for a one-node tree, I put a check in the initializer procedure prune for whether or not a tree was a leaf. Here’s me running a test for that using a single node world-only tree:

Within prune-tree, we return an empty list when a tree is a leaf and otherwise we cons together the datum of the tree with a call to prune-forest with argument children tree.

Within prune-forest, we return the empty list if the forest is null. Otherwise, we cons together the results of a call to prune-tree with car forest and a call to prune-forest with cdr forest. We also filter the results of these calls with not-null?. This cleans up the tree that is generated and prevents it from having a ton of empty lists where the leaves used to be.

world-tree versus pruned world-tree

buntine’s solution

buntine has a cool solution:

My solution does not use the filter operator. Instead if the node is leaf then it just skips over it.
Also I prefer using make-node instead of cons for data encapsulation.

I think the key line he’s talking about re: skipping over a leaf is ((leaf? (car forest)) (prune-forest (cdr forest))). Nice solution!

❌ 18.6

Write a program parse-scheme that parses a Scheme arithmetic expression into the same kind of tree that parse produces for infix expressions. Assume that all procedure invocations in the Scheme expression have two arguments.
The resulting tree should be a valid argument to compute:

(You can solve this problem without the restriction to two-argument invocations if you rewrite compute so that it doesn’t assume every branch node has two children.)

Giving myself no credit here cuz my solution basically reimplemented the existing parse procedure and was super inelegant.

parse-scheme has to be able to handle the following cases:

1. The expression is empty. At this point we’ll be returning our tree.
2. The next value in the expression is an operator. We probably want to make a new tree node here using the operator.
3. The next value in the expression is a list. We’ll probably do a recursive call here.
4. Otherwise, the next value in the expression is a number.

We don’t have to worry about implicit precedence rules with parse-scheme because all the groupings will be explicit. This makes things easier.

Interestingly, the existing parse program seems to handle scheme notation just fine:

So the extremely lazy solution to this question would be something like:

😉

Let’s be more serious though. Suppose we have the expression (* (+ 4 3) 2)). What would we want parse-scheme to do with it?

Well we want it to see that the first value of the expression is *, an operator. If we don’t want to look for operators specifically, we can put this in the else clause as in the original procedure.
Do we want to immediately make a tree using the operator and the next two elements in the expression? No, because as we see in this example, sometimes the next expression might be a sublist. We don’t want to just dump that sublist into our new tree without any processing. So we’ll take our operator and add it to a list of operators, and then make a recursive call to parse-scheme-helper with that operator added to the operator list, and with all but the operator we just added to our list of operators as the value for expr:

(some of this code will be placeholder stuff that I will change as I go along)

We also need to be able to handle numbers. We’ll do so in the same way as in the original procedure:

If we get to the end of an expression, and there are any operators left, we want to “handle” those.

Here’s an unfinished procedure:

It can handle something easy, like (+ 4 3):

Can’t handle nested expressions though.

So let’s make it handle those.

I realized I should make a version of handle-op that actually calls parse-scheme-helper and not parse-helper:

After some more steps and trial and error, I came up with this:

It re-implements a lot of the existing parse procedure but with some notable differences. The order of checking is a bit different, and it doesn’t have the precedence-checking stuff.

buntine’s solution

This is buntine’s solution:

Ah this is so elegant! 😍

For some reason I didn’t consider just making a straight up normal single recursive procedure…

So going through this in detail:

1. check if the expr is null?. if so, return an empty list.
2. check if car expr is a number. if so, cons together leaf (car expr) (turning the number into a leaf node) and the result of a recursive invocation of parse-scheme with cdr expr (which takes us to the next item in the list).
3. check if car expr is a list. If so, cons together the results of a) a recursive invocation of parse-scheme with that list as an argument and b) a recursive invocation of parse-scheme with cdr expr.
4. Otherwise (meaning if car expr is an operator) invoke make-node with car expr as the first argument to make-node. The second argument to make-node will be a recursive invocation to parse-scheme with cdr expr as the argument.