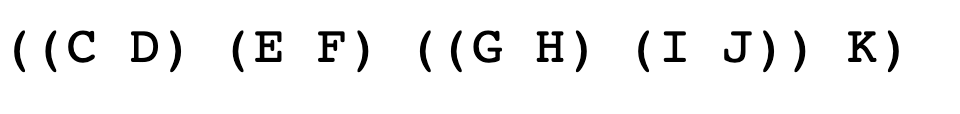Simply Scheme Chapter 17 – Lists

https://people.eecs.berkeley.edu/~bh/ssch17/lists.html

This chapter introduces lists, which are different than sentences. With sentences, every element has to be a word. Lists, by contrast, can contain words, booleans, procedures, or other lists.

Selectors and Constructors

Lists have their own selectors and constructors. car selects the first element of a list, and is the list equivalent of first. cdr selects all but the first element of a list, and is the list equivalent of butfirst.

list is a constructor that takes any number of arguments (of whatever type) and returns a list with those arguments as elements.

cons is a constructor that takes two arguments, an element and an existing list, and returns a list whose car is the first argument and whose cdr is the second argument. The second argument to cons must be a list.

The book describes a procedure, append, which takes the elements of two or more lists and combines them into a larger list. It notably does not describe append as a constructor but uses the word “function”.

The book contrasts the three procedures:

list retains the structure of the information that was put into the procedure. For example, if the second argument is a list, then list retains that info in the form of giving the making the list a sub-list within the new list that it makes.

cons only retains any nested structures for the first argument (the element being added to the second argument, which is an existing list).

append “flattens” the arguments it’s provided into a single list. However, if something is double-nested, it will retain that information.

Programming with Lists

In this example our result is a list of sentences. That is, the result is a list that includes smaller lists as elements, but each of these smaller lists is a sentence, in which only words are allowed. That’s why we used the constructor cons for the overall list, but se for each sentence within the list.
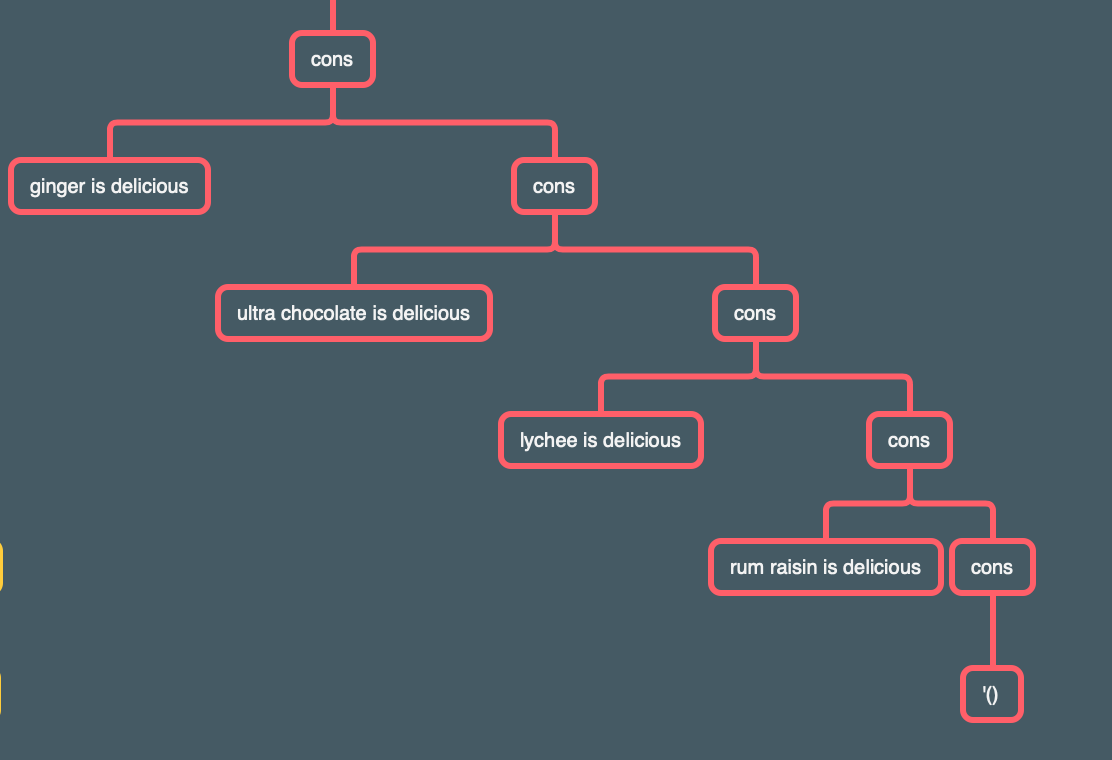
This is the example worth a thousand words that we promised, to show why cons is useful. List wouldn’t work in this situation. You can use list only when you know exactly how many elements will be in your complete list. Here, we are writing a procedure that works for any number of elements, so we recursively build up the list, one element at a time.

If you actually try to use list in place of cons in the praise procedure, you get the following output (which I’ve spaced to make the structure a bit more apparent):

Two big problems here: the structure is deeply nested, and we have an unwanted empty nested list.

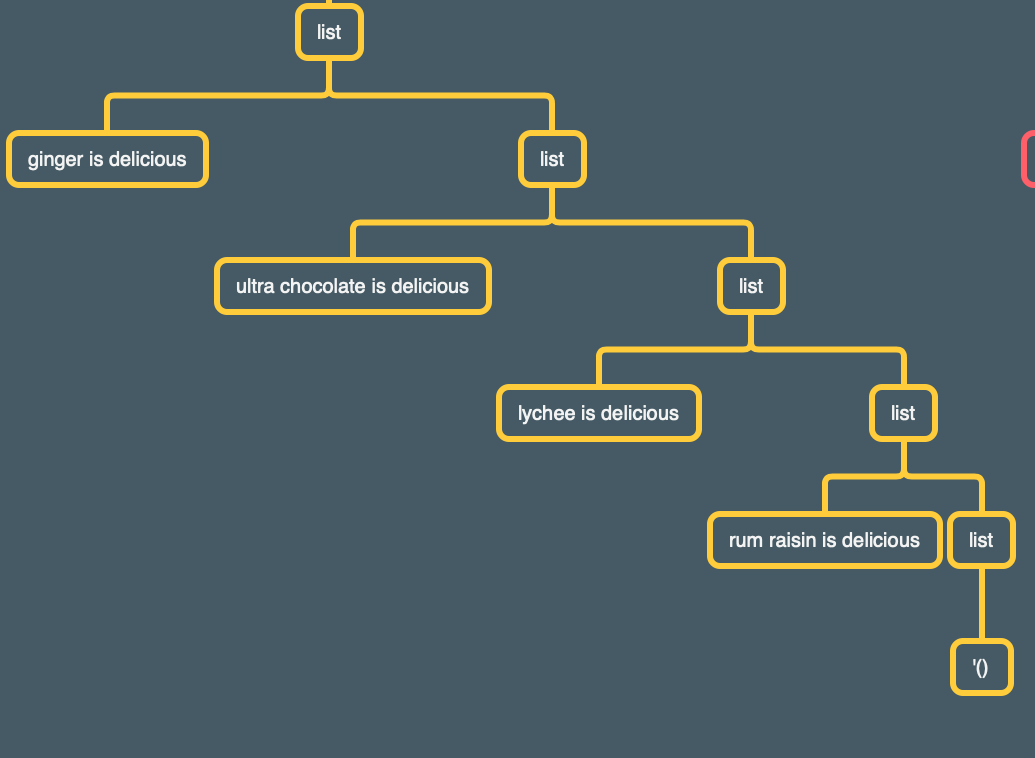
This, by contrast, is the result if you use cons (again formatted to make the structure clearer):

This is a straightforward list with 4 elements.

Why does the first list, made with list, come out bad? Consider the following tree, which is a simplified model of what’s going on in the praise procedure.

So at the very bottom level, one thing to note is that list takes the empty sentence and just treats it like any other argument. That’s why we have an unwanted empty list at the end.

Then, as we move up, we combine rum raisin is delicious with our nested empty list. That gives us (rum raisin is delicious) (), which is still somewhat normal aside from the unwanted (). But then the next level up, we add (lychee is delicious) as the first element and the list (rum raisin is delicious) () as the second element. So rather than keeping each entry as a separate element of the list, we’re starting to have some nesting. The nesting gets worse as we keep going along. ((ultra chocolate is delicious)((lychee is delicious) ((rum raisin is delicious) ()))) has (ultra chocolate is delicious) as the first element of the list, and ((lychee is delicious) ((rum raisin is delicious) ()))) as the second element, and that second element in turn has ((rum raisin is delicious) ())) as its second element. So the nesting is stacking up with each recursive call.

Note that the structure of the recursive calls is the same if we use cons, but the result winds up very different:

When we cons the (), rather than being treated as a thing to be added to a list, the () is treated as an empty list, and so rum raisin is delicious is added to it, so we don’t have that extra (). And then as we move on up the tree of recursive calls, each cons call treats the existing list as a list of things and then proceeds to add the first argument as another list entry at the same “level” as the other ones, rather than piling up a bunch of nesting. So the structure of the procedural calls is the same using either constructor but the result is very different because of the difference in how the two constructors work.

The book mentions that you can use shortcuts like cadar to find the (car (cdr (car of something, and that these work up to 4 letters deep in a’s and d’s.

The Truth about Sentences

You’ve probably noticed that it’s hard to distinguish between a sentence (which must be made up of words) and a list that happens to have words as its elements.

The fact is, sentences are lists. You could take car of a sentence, for example, and it’d work fine.

Sentences are an abstract data type represented by lists.

The idea of abstract data types was introduced in Chapter 16 in the context of the pattern matcher. In that context, we used a sentence separated by ! to represent a database. The database was an abstract data type of name-value associations that we created, and the sentence was the Scheme concept that we used to represent that data type. The big reveal here is that sentences themselves, which we’ve essentially treated as a built-in Scheme data type, are themselves an abstract data type that is represented by lists.

[…] it so happens that Scheme represents lists in a way that makes it easy to find the first element, but harder to find the last one. That’s reflected in the fact that there are no primitive selectors for lists equivalent to last and butlast for sentences. But we want last and butlast to be a part of the sentence package, so we have to write them in terms of the “real” Scheme list selectors. (In the versions presented here, we are ignoring the issue of applying the selectors to words.)

If you look “behind the curtain” at the implementation, last is a lot more complicated than first. But from the point of view of a sentence user, they’re equally simple.

null? is the list equivalent of empty. last is more complicated than first because, given the lack of a built-in way to get to the last element of a list in Scheme, last needs to use recursion plus a null? check in order to actually get to the last element, whereas first can just use the built-in car procedure.

Various Procedures for Lists (Combines content of several subsections)

map is the standard list equivalent of every.

Map takes two arguments, a function and a list, and returns a list containing the result of applying the function to each element of the list.

filter is the standard list equivalent of keep.

Filter also takes a function and a list as arguments; it returns a list containing only those elements of the argument list for which the function returns a true value. This is the same as keep, except that the elements of the argument list may be sublists, and their structure is preserved in the result.

reduce is the standard list equivalent of accumulate.

list? tests if an argument is a list.
equal? works on lists.
length is the list equivalent of count.
list-ref is the list equivalent of item:

it’s different in that it counts items from zero instead of from one and takes its arguments in the other order:

member, as distinct from member?, works a bit differently than member? does:

Scheme does have a member primitive without the question mark that’s like member? except for two differences: Its second argument must be a list (but can be a structured list); and instead of returning #t it returns the portion of the argument list starting with the element equal to the first argument. This will be clearer with an example:

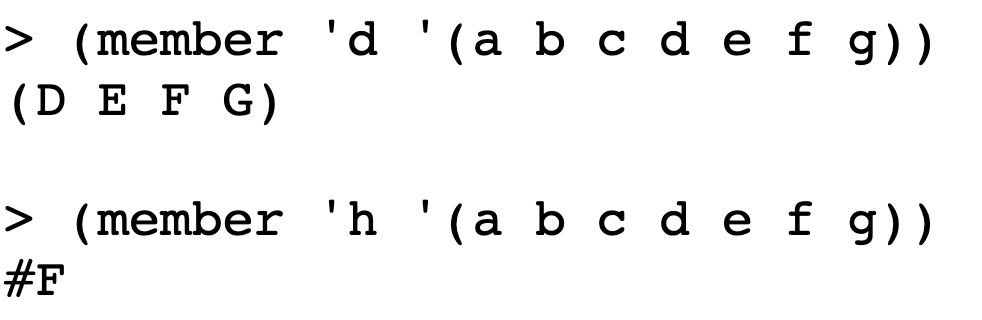
This is the main example in Scheme of the semipredicate idea that we mentioned earlier in passing. It doesn’t have a question mark in its name because it returns values other than #t and #f, but it works as a predicate because any non-#f value is considered true.

assoc can look up a name in an association list:

A list of names and corresponding values is called an association list, or an a-list. The Scheme primitive assoc looks up a name in an a-list:

assoc returns false if there’s no match.

They give an example of assoc being used:

Functions That Take Variable Numbers of Arguments

Here’s a procedure that takes one or more numbers as arguments and returns true if these numbers are in increasing order:

The . is something you can use before the last parameter to indicate that that final parameter represents any number of arguments. The number of arguments before the . determines the minimum number of arguments, and zero is a valid option.

The other thing of note is apply, which takes two arguments: a procedure and a list.

Apply invokes the given procedure with the elements of the given list as its arguments, and returns whatever value the procedure returns. Therefore, the following two expressions are equivalent:

The above are equivalent because + can take multiple arguments. If you try to invoke apply with a list that has 2 or more items when the procedure you’re using for the first argument to apply can only take one argument, you’ll get an error message:

We use apply in increasing? because we don’t know how many arguments we’ll need in its recursive invocation. We can’t just say

because that would give increasing? a list as its single argument, and it doesn’t take lists as arguments-it takes numbers. We want the numbers in the list to be the arguments.

Here’s a trace on increasing? as they wrote it:

And here’s a trace for when the code has been edited to replace apply increasing rest-of-numbers with increasing? rest-of-numbers

You can see how in the second version, the list has been provided to increasing as a single argument. If we change the input to (increasing? 4 12 11 82) it actually gives the wrong result:

This input should return #f but is returning #t.

The reason increasing? is returning true in the examples where I’ve changed the coder and an entire list is being passed to increasing? is: in the recursive call where the entire list is passed to increasing?, that list becomes number, which means rest-of-numbers is an empty list. The first check increasing? does is for whether rest-of-numbers is empty, and if so, increasing? returns true. So it’s very key to use apply here or you really mess up the whole procedure.

Recursion on Arbitrary Structured Lists

The book discusses this procedure:

This is quite different from the recursive situations we’ve seen before. What looks like a recursive call from deep-appearances to itself is actually inside an anonymous procedure that will be called repeatedly by map. Deep-appearances doesn’t just call itself once in the recursive case; it uses map to call itself for each element of structure. Each of those calls returns a number; map returns a list of those numbers. What we want is the sum of those numbers, and that’s what reduce will give us.

map first argument is the lambda function and its second argument is a list. deep-appearances uses the map and lambda to keep “digging” within a nested list structure until hitting a word (which is the base case).

The book describes deep-appearances as one way of organizing programs to deal with lists of a sublist. But it says there’s another style:

Here’s the idea. We deal with the base case-words-just as before. But for lists we do what we often do in trying to simplify a list problem: We divide the list into its first element (its car) and all the rest of its elements (its cdr). But in this case, the resulting program is a little tricky. Ordinarily, a recursive program for lists makes a recursive call for the cdr, which is a list of the same kind as the whole argument, but does something non-recursive for the car, which is just one element of that list. This time, the car of the kind of structured list-of-lists we’re exploring may itself be a list-of-lists! So we make a recursive call for it, as well:

Since we have to take into account the possibility that car structure is a list-of-lists, we need to make a recursive call for it as well, so that we make sure we go as deep as we need to on the car structure “branch” of our structure.

This procedure has two different kinds of base case. The first two cond clauses are similar to the base case in the previous version of deep-appearances; they deal with a “structure” consisting of a single word. If the structure is the word we’re looking for, then the word appears once in it. If the structure is some other word, then the word appears zero times. The third clause is more like the base case of an ordinary list recursion; it deals with an empty list, in which case the word appears zero times in it. [..]
If we reach the else clause, then the structure is neither a word nor an empty list. It must, therefore, be a non-empty list, with a car and a cdr. The number of appearances in the entire structure of the word we’re looking for is equal to the number of appearances in the car plus the number in the cdr.

What if we want to build list-of-list structures? The book gives an example:

The book contrasts deep-pigl with praise and notes that:

Praise is a simple left-to-right walk through the elements of a sequence; deep-pigl dives in and out of sublists. The difference is a result of the fact that praise does one recursive call, for the cdr, while deep-pigl does two, for the car as well as the cdr.

Pitfalls

The book recommends against using list as a formal parameter and suggests lst, L, or seq as alternatives.

If you mix up the order of arguments in cons, you may get funny looking results:

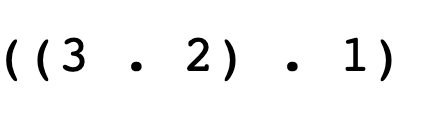
Boring Exercises

✅17.1

What will Scheme print in response to each of the following expressions? Try to figure it out in your head before you try it on the computer.

(car '(Rod Chris Colin Hugh Paul))

I predicted Rod. I was correct.

(cadr '(Rod Chris Colin Hugh Paul))

I predicted Chris. I was correct.

(cdr '(Rod Chris Colin Hugh Paul))

I predicted (Chris Colin Hugh Paul). I was correct.

(car 'Rod)

Wasn’t sure about this one. Rod isn’t a list, but a word, so it might give an error message. If there’s something within car that tells it to just return whatever argument it’s provided if the argument is a list, it might return Rod. If there’s something within car that treats words as a list of characters, it might return R.

Here’s what happened:

pair? was not an error message I expected. I don’t understand why that particular error message showed up.

I predicted '((Rod Argent) Chris White). I was correct.

I predicted '(Rod Argent Chris White). I was correct.

I predicted '((Rod Argent) (Chris White)). I was correct.

I predicted Chris. I was correct.

I predicted '(Colin Blunstone). I was correct.

I think assoc may only check the first value for a match, so it may return #f here. That is my tentative guess. The other possibility is that it will return (Rod Argent).

It returned #f.

✅17.2

For each of the following examples, write a procedure of two arguments that, when applied to the sample arguments, returns the sample result. Your procedures may not include any quoted data.

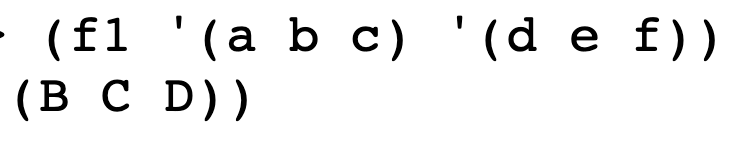
Here’s my answer:

We need to turn the result of car lst2 into a list for append to work, hence my use of list.

My answer:

list takes the cdr lst and drops it in as a sublist, which is what we want here.

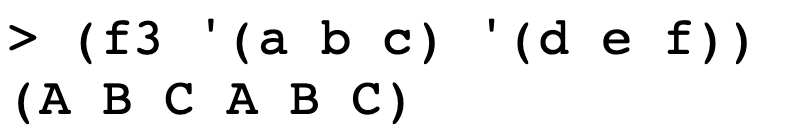
My answer:

My answer:

🤔❓17.3

Describe the value returned by this invocation of map:

Hmm 🤔

Let’s recall the fact that:

Map takes two arguments, a function and a list, and returns a list containing the result of applying the function to each element of the list.

My initial intuition was that the procedure for exercise 17.3 should return a list of the results of adding up x and y. So something like '(3 5 7). That clashes with the definition of map, though, which is that it is the result of applying a function to each element of a list.

Consider this procedure:

That lines up with my expectations.

And that’s like the output for 17.3.

Or consider this:

Lambda is returning a procedure which checks whether the input is even?.

And here it just returns #<procedure>.

I don’t have a full explanation of what’s going on, but I think part of the issue may be that map is trying to apply a two-variable expression (+ x y) when it just goes through the list one element at a time. So there’s like a mismatch between the number of arguments being provided to the procedure and the number of arguments the procedure wants. That’s a low-confidence guess though.

I checked the blog of Brittney Ten Cate, someone who also did this exercise, but they didn’t know either. :-\

Real Exercises

✅ 17.4

Describe the result of calling the following procedure with a list as its argument. (See if you can figure it out before you try it.)

So mystery calls mystery-helper with the original lst and an empty list as arguments.

Within mystery-helper, if the lst is null?, other is returned. Otherwise, a recursive call is made. All but the last element of the list is provided as the first argument, and the car of the lst is cons‘ed together with other as the second argument.

So if we had the initial input as a list (a b c), then the first recursive call to mystery-helper would have (b c) and (cons 'a '()) (or (a)) as the arguments, and then the next recursive call would have (c) and (b a) as the arguments, and then the final would be () and (c b a) as the arguments, and then lst would be empty and so we’d return (c b a), or the reverse of the initial input.

Checking:

Yep 🙂

✅ 17.5

Here’s a procedure that takes two numbers as arguments and returns whichever number is larger:

Use max2 to implement max, a procedure that takes one or more numeric arguments and returns the largest of them.

Answer:

Base case is when we’re out of rest-of-numbers, in which case we return our surviving number.

Otherwise we apply max to (as the first argument to max) the “winner” of calling max2 on number and the first number of rest-of-numbers and (as the second argument to max) the cdr of rest-of-numbers.

And here’s a trace that shows it in operation:

We use apply cuz otherwise this happens:

✅❌ 17.6

Implement append using car, cdr, and cons. (Note: The built-in append can take any number of arguments. First write a version that accepts only two arguments. Then, optionally, try to write a version that takes any number.)

So this is what we want to happen:

Ok here’s my two argument version:

butlast and last seemed like they might be fair game to use since we now know they’re built from car, cdr, and cons based on the information from the chapter. I wasn’t sure though, and had an intuition that solving the problem might be possible without them.

The basic idea is append2 recursively calls itself with the first argument being all but the last element of L1 and the second argument being the cons of the last element of L1 and the entirety of L2. This slowly adds the contents of L1 to L2 from the “right” side of L1 to L2 until L1 is empty. At that point, we return L2.

I made append3, which handles any number of arguments, using append2:

Other Solutions

I checked for other solutions cuz I had some inkling I was missing something simpler.

First I checked Brittney Ten Cate’s site:

I think they misunderstood the instructions. The book wanted the reader to write an implementation of append. That implementation shouldn’t use append itself. Also it doesn’t work:

Next I checked buntine, who’s generally pretty on-point:

This is way more on the right track than Autodidact’s answer but still doesn’t work right. The order is wrong.

ponsgsh’s Solution & Detailed Analysis

Ok let’s try pongsh

This one works!

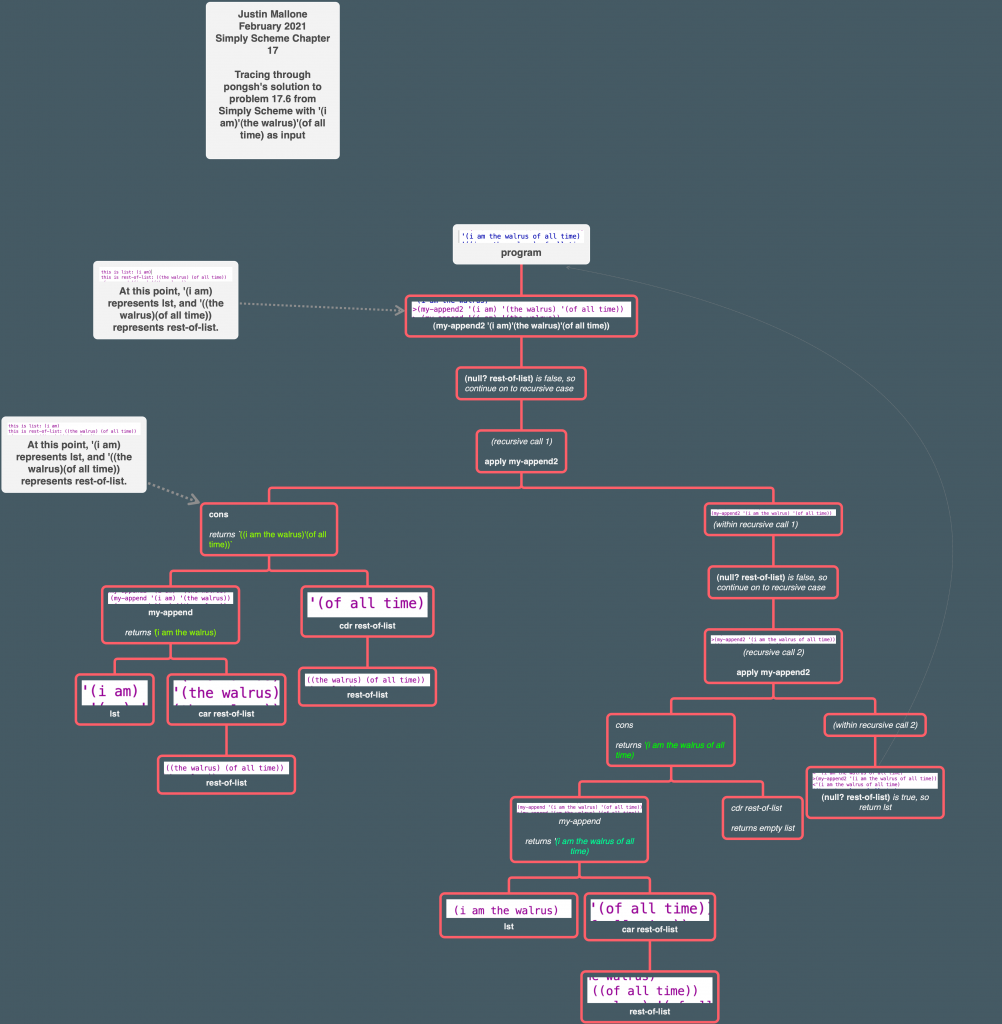
Note that he didn’t need to use last or butlast. How does his version work?

for my-append, he does cons with car lst as the first argument, and recursively calls my-append with cdr lst as the first argument and lst2 as the second argument. So we’re pulling apart the elements of lst1 one at a time until we run out, and then we’re returning lst2 in the base case, and then reassembling the elements of lst1 “back to front” because of how we structured the recursive calls. So this avoids the necessity of having to use last or butlast.

my-append2 makes use of my-append. If rest-of-list is empty, it returns lst. Otherwise, it applies a recursive call of my-append2 to a list. The list is formed by cons. cons takes my-append lst (car rest-of-list) as the first argument and cdr rest-of-list as the second. So if you give my-append2 three lists, it will first use my-append to combine the first two lists together. If the first two arguments are (i am), and the (the walrus), my-append will combine those:

That combined argument '(i am the walrus) is then used as the first argument to cons, with the second argument being cdr rest-of-list, which I think will be (of all time). What I’m not sure about at this point is why using a list as an argument to cons would be okay. I would expect to get unwanted list nesting as was depicted earlier in the chapter:

I think I should step through this with a tree.

I made a variant of pongsh’s program with some display statements:

This particular line stood out to me:

For some reason I was thinking of ((of all time)) as being singly nested, so I expected the value for rest-of-list to be (of all time) rather than ((of all time)). Then i was thinking that cdr rest-of-list would grab it as of all time, and so when cons was invoked, you’d get the result ((i am the walrus) of all time). That’s where I was getting stuck.

But rest-of-list is a list-of-lists of in which the lists are nested. When the procedure starts out, the rest-of-list list has two nested entries:

if you take cdr of rest-of-list at the time, you don’t get of all time but (of all time). If you invoke cons on a list and the cdr of a nested list where there’s a second value, you get a list with two sublist elements:

Because I was unclear on the precise nature of the value being returned by cdr rest-of-list, I was confused as to how the procedure was able to function correctly, but this analysis has fixed my misconception.

I’m going to give myself half credit for this problem because I sort of solved it but I’m not quite sure I solved it in a way that was intended. I think I learned a lot from analyzing pongsh’s solution though 🙂

Here’s a tree I made while figuring out how pongsh’s procedure worked:

✅ 17.7

Append may remind you of sentence. They’re similar, except that append works only with lists as arguments, whereas sentence will accept words as well as lists. Implement sentence using append. (Note: The built-in sentence can take any number of arguments. First write a version that accepts only two arguments. Then, optionally, try to write a version that takes any number. Also, you don’t have to worry about the error checking that the real sentence does.)

Let me try iterating my way to a working procedure for this one.

So here’s a very naive non-working version to start:

It works for sentence…

…but not for words:

The solution that occurred to me is to check for the inputs being not-lists and then turn them into lists and recursively call the procedure with the new list form of the input:

I’m assuming that we only give sentence2 lists or words.

🙂

Here’s the version for any number, which builds on sentence2:

🙂

buntine’s Solution & Detailed Analysis

buntine:

His sentence2 is pretty similar to mine in some ways. Rather than checking if something is not a list, though, he checks if it is a word (this is probably better as it seems simpler). He also breaks out the turning-the-word-into-a-list functionality into a separate helper procedure rather than using cons with the word and an empty list. The listify procedure checks whether each element within a list is a word. If it is, it calls list on it to turn it into a list; otherwise, it returns it. This lets you go through a mixed list of words and sentences and transform the non-lists into lists:

The image above is from a trace on listify. I was a bit thrown off because initially when I tried to play with listify with a test list I didn’t get the result I expected:

I was using ' marks before the words. That caused them to not be treated as words by listify. That’s counterintuitive because:

I made a modified version of buntine’s listify procedure with some display statements added to get a look inside the procedure:

So as you can see, if word? l returns true, we’ll get to see what the content of l is.

Here’s me running a trace for my modified listify with a no-apostrophe-before-words version of my test list (trace is in purple):

And here’s me running the same thing but where there are apostrophes before the words of the test list:

So you can see that the (if (word?) l) line isn’t returning true and turning the “words” into lists because they are not registering as words.

Another modification to the procedure:

And we run it when testflight has some words with apostrophes in front of them:

The apostrophe in Scheme stands for the quote procedure, as discussed in chapter 5.

When using quote around a group of values surrounded by parentheses (what we’ve been calling a sentence), each individual value within the group registers as a word:

However, if we add another quote nested within, the quoted (or double-quoted) value doesn’t register as a word:

What happens when we double-quote potato? Pretty much what you would expect:

So I think maybe I was effectively double-quoting within my test list that had the words separately quoted, because the entire list was already quoted and so each separate word-value within the list was already a word for word? purposes and didn’t need an additional quote. And in fact when I added an additional quote, I did something that made it so that it would no longer count as a word.

When I do word? potato there’s no quoting around potato so it registers as undefined:

Compare:

When we’re looking at (potato) as a whole, that’s not a word but a sentence.
When we’re looking at potato as an element within the sentence (potato), then potato is a word. Note that in the latter case potato doesn’t have a ' directly in front of it on the inside, but is still in fact a word.

✅ 17.8

Write member.

The desired outcome:

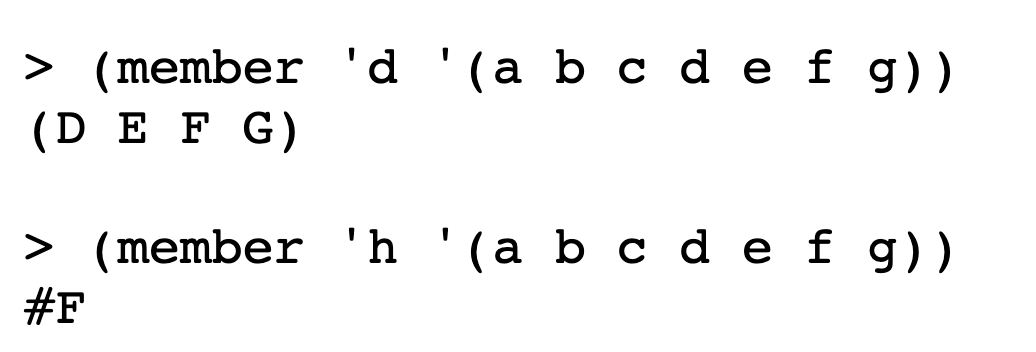
My answer:

The program in action, with some trace:

Looks good!

Could have done it using cond as well of course:

✅ 17.9

Write list-ref.

Refreshing myself on list-ref:

The only word-and-sentence functions that we haven’t already mentioned are item and count. The list equivalent of item is called list-ref (short for “reference”); it’s different in that it counts items from zero instead of from one and takes its arguments in the other order:

My answer:

✅ 17.10

Write length.

✅ 17.11

Write before-in-list?, which takes a list and two elements of the list. It should return #t if the second argument appears in the list argument before the third argument:

My answer:

The idea is that member returns the list from the point at which the argument to member is found, so the earlier argument will generate a longer list with more elements, and thus will have a larger length. I didn’t see anyone else with this particular solution. 🙂

✅ 17.12

Write a procedure called flatten that takes as its argument a list, possibly including sublists, but whose ultimate building blocks are words (not Booleans or procedures). It should return a sentence containing all the words of the list, in the order in which they appear in the original:

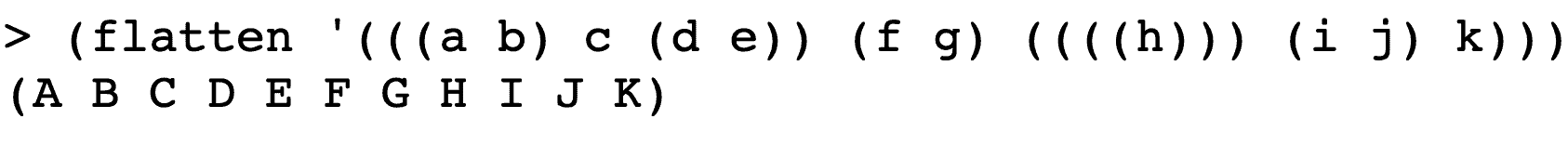
Answer:

Analysis:

If structure is a word, return it. Otherwise, invoke reduce with se as the function. the (map (lambda (sublist) (flatten sublist)) structure) expression invokes flatten repeatedly inside the anonymous lambda expression and does so for each element of the structure, and continues “drilling down” until a word is reached in the base case. Then all the words are accumulated together with reduce se into a list with no nesting.

Here’s a trace of part of the drilling down, on the first sublist in the example:

✅ 17.13

Here is a procedure that counts the number of words anywhere within a structured list:

Although this procedure works, it’s more complicated than necessary. Simplify it.

This is more than a simplification of the existing procedure but it is simpler:

The reduce line creates an invocation of deep-count for each sublist, saving us the trouble of having to work our way through two parts of lists with car and cdr.

Because we’re just returning a 1 when we hit a list rather than navigating through lists using car and cdr, we never hit an empty list and so we don’t have to worry about that case.

buntine’s solution

Note that I’ve modified buntine’s solution because I think it’s missing an essential value; it has like a typo or something:

He kept the cond structure but simplified the structure by incorporating reduce.

✅ 17.14

Write a procedure branch that takes as arguments a list of numbers and a nested list structure. It should be the list-of-lists equivalent of item, like this:

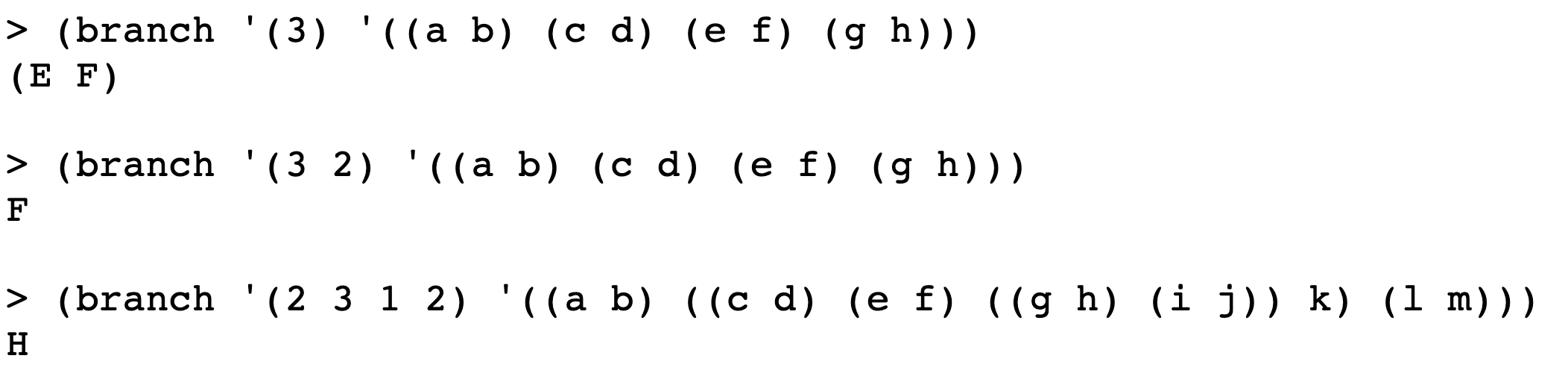
In the last example above, the second element of the list is

The third element of that smaller list is ((G H) (I J)); the first element of that is (G H); and the second element of that is just H.

Answer:

If we’re on the last num, list-ref gets called with lst as the first argument and num minus 1 as the second argument (branch starts counting from 1, but list-ref starts counting from zero, so we have to translate between the two.)

Otherwise, we recursively call branch with all but the first num as the number argument and with the appropriate branch of the list, based on the first num, as our second argument.

pongsh’s solution

I liked pongsh‘s solution:

He made the empty list the base case rather than making it when lst-num equals 1, and this lead to a more elegant base case. His recursive case is structurally identical.

🤔17.15

Modify the pattern matcher to represent the known-values database as a list of two-element lists, as we suggested at the beginning of this chapter.

Skipping over this one for now. I find modifying the pattern matcher pretty hard due to the number of moving parts. Also, everyone else that I know of with answers posted online skipped it, so that makes it harder to check/compare my answer. I might return later.

✅ 17.16

Write a predicate valid-infix? that takes a list as argument and returns #t if and only if the list is a legitimate infix arithmetic expression (alternating operands and operators, with parentheses-that is, sublists-allowed for grouping).

My answer:

valid-infix just serves to pass valid-infix-helper a flattened version of the initial list.

flatten works much like the solution to 17.12, except that it also checks for the case where a value is an operator? (like +, /, *, or -) in addition to checking if it’s a word?.

operator? is pretty self explanatory.

valid-infix-helper first cond clause checks whether the last remaining value in a flattened list is a number. If so, it returns #t. This is the base case.

The second cond clause checks whether the car and cadr of the flattened list are a number and operator, respectively. If so, it recursively calls itself without those values.

Otherwise it returns #f.

buntine’s solution

Wanted to go through someone else’s solution since my flatten approach seemed like kind of a hack:

Someone else had the idea to make an operator? function 🙂

recur-or-die seems to return false unless pred exists/returns true. If pred does return true, then infix-helper is invoked with two arguments: car lst and cdr lst respectively.

infix-helper is where the main action is. From valid-infix it receives car lst as its prev and cdr lst as its lst. So the list has already been broken up a bit by the time it gets to infix-helper. First cond returns true if the lst is empty; makes sense. Then it checks if car lst is a number. And now we see how recur-or-die works. operator? prev is passed in as the pred to recur-or-die. So if car lst is a number but then prev isn’t an operator, recur-or-die returns #f. On the other hand, if car lst is a number and prev is an operator, recur-or-die calls infix-helper with car lst and cdr lst as the respective two arguments. Because the original lst passed to infix-helper already had had the first value of the original list broken out separately into prev, this subsequent breaking up of the list further “moves us through” the list. Here’s an example of what I mean:

the “4” was already broken out from the list when passed by valid-infix? to infix-helper. And now we’ve broken off the “+” as well.

infix-helper‘s third cond line does a similar test as the second, this time for whether car lst is an operator. This time, the first argument passed to recur-or-die is (or (number? prev)(list? prev)). In the following screenshot from trace, car lst of lst in infix-helper is an operator, so my-list? (an alias forlist?i made so I could run trace on it) is invoked:

The final cond tests whether car lst is a list?. If so, it checks whether prev is an operator and whether valid-infix? (car lst) is true. That latter part seems key for handling expressions nested in parentheses.

I think I have some idea of how buntine’s solution works now.