Simply Scheme Chapter 15 – Advanced Recursion

Example – Sort

This is the first example in this chapter of a procedure. It takes a sentence and returns a sentence with the same words in alphabetical order. I partially figured out how it works myself after reading some of the chapter. The only slightly tricky part was earliest-helper. remove-once is from a previous chapter.

Example – From-Binary

We want to take a word of ones and zeros, representing a binary number, and compute the numeric value that it represents. Each binary digit (or bit) corresponds to a power of two, just as ordinary decimal digits represent powers of ten. So the binary number 1101 represents (1×8)+(1×4)+(0×2)+(1×1) = 13. We want to be able to say

Here was my solution

In english:

Base case: if num is empty, return 0.
Recursive case: if the first digit of the binary number is equal to 1, then figure out the appropriate decimal equivalent for that digit. This is done by taking 2 and raising it to the appropriate power, determined by the length (count) of num minus 1. Sum that with the results of a recursive call to from-binary with all but the first digit of num.
If the first digit is not 1, then just recursively call from-binary with all but the first digit of num.

The book did it a bit differently.

Here is their first version:

I found this bit particularly notable:

They are multiplying first bits and the expt part together, and then summing the result. So when the first digit is 0, that will get multiplied together with the (expt 2 (count (bf bits))) and turn that into 0, so it won’t get added to the total. And when the first digit is 1, the result of expt does get added to the total.

Then they say:

Although this procedure is correct, it’s worth noting that a more efficient version can be written by dissecting the number from right to left. As you’ll see, we can then avoid the calls to expt, which are expensive because we have to do more multiplication than should be necessary.

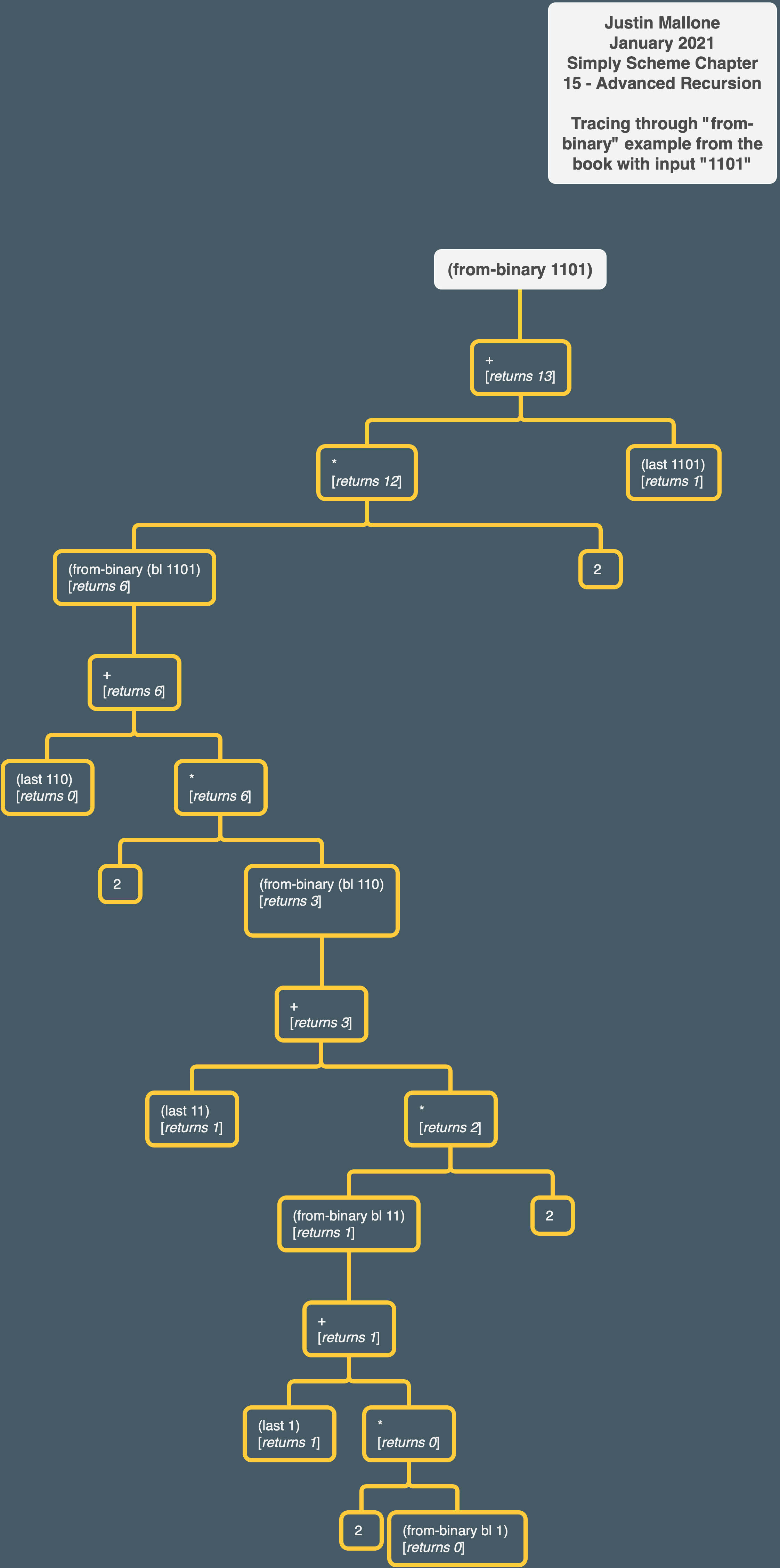
Suppose we want to find the value of the binary number 1101. The butlast of this number, 110, has the value six. To get the value of the entire number, we double the six (because 1100 would have the value 12, just as in ordinary decimal numbers 430 is ten times 43) and then add the rightmost bit to get 13. Here’s the new version:

This version may look a little unusual. We usually combine the value returned by the recursive call with some function of the current element. This time, we are combining the current element itself with a function of the recursive return value. You may want to trace this procedure to see how the intermediate return values contribute to the final result.

The results of trace from-binary with their new version:

still a bit fuzzy so let me step through the program step by step with the 1101 example.

Ok so let’s say we get to the point where the recursive call to from-binary is going to return 0 because we’ve bl‘ed through the number and we’re down to the 1 that is at the beginning of the number:

substituting:

and again:

So the final call recursive call returns 0 and the call “above” that one in the recursive chain of calls returns 1 because of the value of the last digit.

what about when the recursive call is on the first two digits of 1101, 11? Since the recursive call “below” that level returned 1, then by the logic of our program the level “above” that will return 3:

Now we get to the point where the 0 is the digit that will be returned by last bits. Because the “lower level” of recursive call below this level will return three, and last bits will return 0, this level of our procedure will return 6:

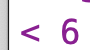
If the original number had been 1111, then this level of the procedure would return 7:

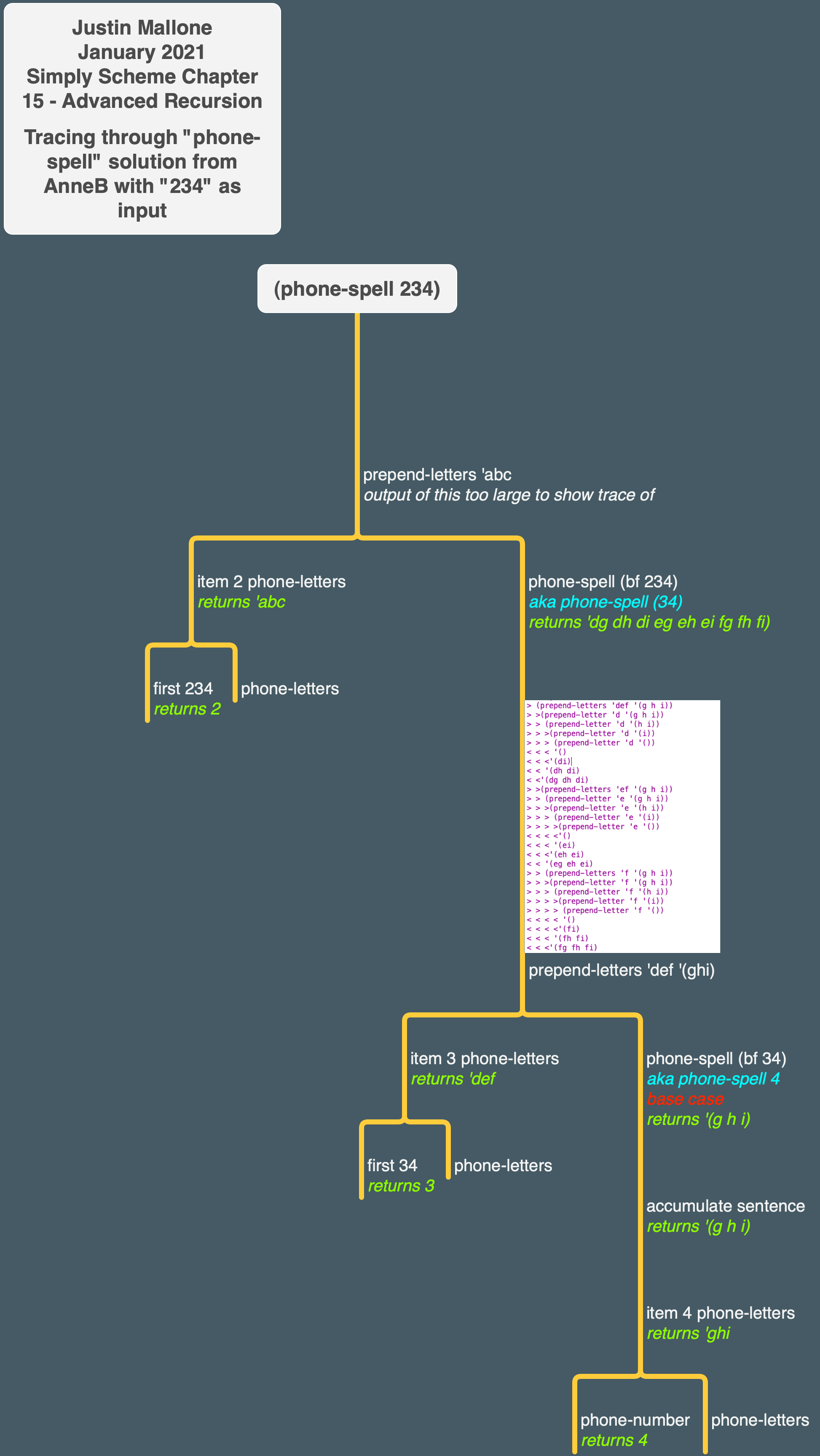
Finally, at the “highest” level of the procedure, since the lower level of recursive call returned 6, and the final digit is 1, the overall procedure will return 13:

Here’s a tree showing this hierarchy stuff visually:

Example – Mergesort

Let’s go back to the problem of sorting a sentence. It turns out that sorting one element at a time, as in selection sort, isn’t the fastest possible approach. One of the fastest sorting algorithms is called mergesort, and it works like this: In order to mergesort a sentence, divide the sentence into two equal halves and recursively sort each half. Then take the two sorted subsentences and merge them together, that is, create one long sorted sentence that contains all the words of the two halves.

This is their half-finished code version of the above:

merge is a necessary helper procedure for mergesort.
This is the book’s version of the merge procedure we wrote for exercise 14.15:

I won’t explain how this works again since I went into it in some detail before.

Now we have to write one-half and other-half. One of the easiest ways to do this is to have one-half return the elements in odd-numbered positions, and have other-half return the elements in even-numbered positions. These are the same as the procedures odds (from Exercise 14.4) and evens (from Chapter 12).

Example – Subsets

We’re now going to attack a much harder problem. We want to know all the subsets of the letters of a word-that is, words that can be formed from the original word by crossing out some (maybe zero) of the letters. For example, if we start with a short word like rat, the subsets are r, a, t, ra, rt, at, rat, and the empty word (""). As the word gets longer, the number of subsets gets bigger very quickly.[3]

As with many problems about words, we’ll try assuming that we can find the subsets of the butfirst of our word. In other words, we’re hoping to find a solution that will include an expression like

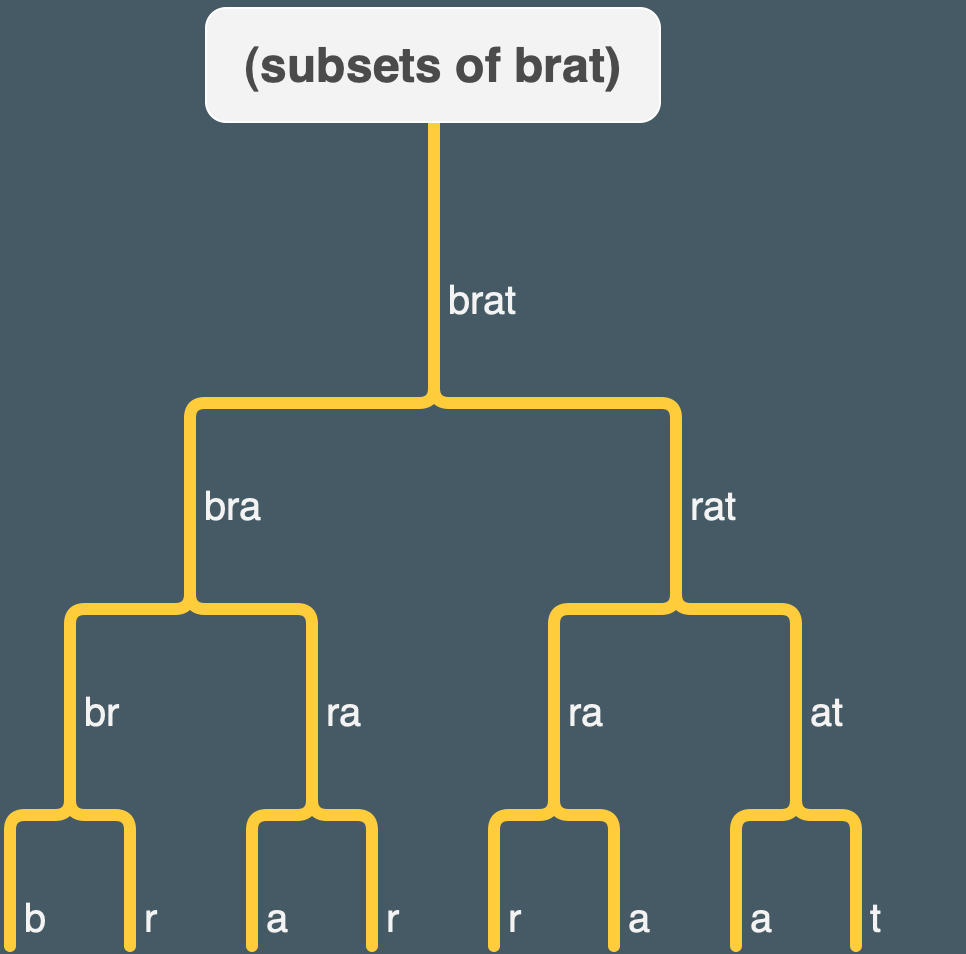
Let’s actually take a four-letter word and look at its subsets. We’ll pick brat, because we already know the subsets of its butfirst. Here are the subsets of brat:

You might notice that many of these subsets are also subsets of rat. In fact, if you think about it, all of the subsets of rat are also subsets of brat. So the words in (subsets 'rat) are some of the words we need for (subsets 'brat).

Here’s a quick tree showing a hierarchy of some subsets of brat excluding the empty word. It doesn’t have stuff that skips over a letter, though (like “brt”).

note that there is duplication between subsets (e.g. “ra” or the single letters “a” and “r”).

ADDENDUM: this tree may actually be more relevant for thinking about Exercise 15.3.

Let’s separate those out and look at the ones left over:

Right about now you’re probably thinking, “They’ve pulled a rabbit out of a hat, the way my math teacher always does.” The words that aren’t subsets of rat all start with b, followed by something that is a subset of rat. You may be thinking that you never would have thought of that yourself. But we’re just following the method: Look at the smaller case and see how it fits into the original problem. It’s not so different from what happened with downup.
Now all we have to do is figure out how to say in Scheme, “Put a b in front of every word in this sentence.” This is a straightforward example of the every pattern:

The way we’ll use this in (subsets 'brat) is

Of course in the general case we won’t have b and rat in our program, but instead will refer to the formal parameter:

Ah I see. I think that maybe I was thinking about the program from the wrong angle. I was thinking of breaking down the input word into smaller and smaller subsets (which is kind of what my tree earlier was getting at). But here it seems like we’re building up from the bottom by prepending stuff. E.g. if you have the empty word as the sent for prepend-every and then append t to that, you now have the sentence'(t). And if you have a sentence like '(t "") and then prepend a to each of those elements, then you have '(at a). So the words are getting “built up” as we go along (though there’s the issue of where the empty word is coming from to be prepended to at each step, I’m not clear on that yet but maybe it’s coming).

We still need a base case. By now you’re accustomed to the idea of using an empty word as the base case. It may be strange to think of the empty word as a set in the first place, let alone to try to find its subsets. But a set of zero elements is a perfectly good set, and it’s the smallest one possible.
The empty set has only one subset, the empty set itself. What should subsets of the empty word return? It’s easy to make a mistake here and return the empty word itself. But we want subsets to return a sentence, containing all the subsets, and we should stick with returning a sentence even in the simple case.[4] (This mistake would come from not thinking about the range of our function, which is sentences. This is why we put so much effort into learning about domains and ranges in Chapter 2.) So we’ll return a sentence containing one (empty) word to represent the one subset.

Ok, so when subsets has an empty word, it returns the empty word "" in a sentence. And when prepend-every has an empty sentence, it returns the empty sentence.

Still fuzzy on how all this works, so let’s look at an example – (subsets 't).

Let’s step through this.

This is the result of both recursive calls to subsets in the recursive case. The procedure needs the results of these calls in order to perform further operations. After the recursive calls have been made, and first wd evaluated, the situation is as follows:

OK now I’m starting to get it. The first recursive call to subsets – the one that doesn’t take place within prepend-every – is what gets us the empty word that doesn’t get prepended with the letter “t”. That was something that wasn’t clear to me until now.

When prepend-every gets invoked in the above example, it prepends t to the empty word and returns '(t). prepend-every also has its own recursive call to itself, but it immediately reaches the base case on the input sentence '("") and returns an empty sentence. The empty sentence is the identity element for sentence, and disappears immediately when passed as an argument to se within prepend-every.

This program is entirely correct. Because it uses two identical recursive calls, however, it’s a lot slower than necessary. We can use let to do the recursive subproblem only once:[5]

Yeah I definitely see how the let saves work here.

Exercises

✅❌ Exercise 15.1 – to-binary

First Attempt

Write a procedure to-binary:

I found this really hard for some reason. I think it was partially cuz I had trouble keeping track of the various things I wanted to keep track of in how I wanted to go about solving it and confused myself.

For input ilke 1001, I think the procedure should do something like the following:

1. Figure out that 2^3, or 8, is a power of 2 that we need to represent in the binary version as the first “1”
2. Figure out that 2^2 and 2^1, or 4 and 2, respectively, are not needed in the binary version and that the values for these numbers in their respective places in the binary system should be “0”
3. Figure out that 2^0, or 1, is a power of 2 that we need to represent in the binary version as the final “1”

The first part of step 1 is pretty easy.

This procedure will take a number and return the highest power of 2 (in the form of the plain number – e.g. for 2^3 it will return 8) that does not exceed the number.

The next step should be something like: :

1. generate a 1 and subtract the power of 2 from number
2. test if the next lowest power of 2 below the previous one is less than the new number. if not, generate a 0, and then test the next lowest power of 2. if so, generate a 1, subtract the new power of 2, and then move onto the next lowest power of 2.

This was an early attempt that was starting to get somewhere, wasn’t quite right though:

Here’s where I actually start to get somewhere. This works for the test cases but not for numbers that are actual powers of 2:

This one is getting closer on powers of 2 but has 1 digit too few on them.

I wound up changing the > in the first line of the cond to a > and got that to work:

My intuition is that this is not well organized and fragile and I don’t understand it well, so I’m going to come back to it later after doing some other stuff and try to revise it.

Analysis Regarding Difficulty of Solving This Exercise

Ok some potential problems in my last attempt:
1. Maybe I’m thinking about the problem the wrong way in some fundamental respect
2. Maybe I’m jamming too much into binary-maker (seems likely just by looking at it)
3. I definitely spent too much time “grinding my gears”
4. Not enough thinking, too much “tweak and trace” (“tweak and trace” used to be my default way of trying to write programs. Terrible method. Mostly don’t do it anymore, but still comes up sometimes when I’m stuck)
5. Not looking enough for inspiration from from-binary?

Second Attempt

So let’s think about a new approach. How about:

Based on the result of something like power-2-helper, we figure out how many digits the binary number will have and set the first 1 to “1”, and then subtract the value of that first power of 2 from the number. Then, we “flip” each of 0’s remaining in the number to “1” if the power of 2 that corresponds to them can be subtracted from the remaining number.

My initial stab with this approach was this:

It got me the intermediate result I wanted, e.g. for input of 9 it gives:

Already I’m feeling better about this approach.

Oh btw, I found inexact->exact online, pretty cool procedure.

So with this approach I sort of got somewhere, but still was having trouble with exact powers of 2, and it still seemed overly complicated:

I get the correct output for 9 and 23, but for the input 16 I just get “1”.

The functionality at least seems more broken out and better organized, which addresses one of the issues I mentioned.

Third Attempt

Okay now for a different attempt.

Figure out power of 2 that’s below number. Subtract value of power of 2 from number. Then compare values — if next power 2 down is less than the remaining number, generate a 1, and if the next power of 2 down is more than the remaining number, generate a 0:

Happiest with this attempt so far but it still can’t handle powers of 2.

Fourth Attempt (Success!)

(I’m only giving myself partial credit due to extreme inelegance)

I asked for help in the #technical chat of the Fallible Ideas Discord server:

Thanks to AnneB and curi for the advice, it was helpful!

Here is me going through some examples by hand:

And this is my attempt to describe the general case of the problem in English:

to-binary will take a number as input and return a binary version of that number as output. It will call binary-generator with the number and the highest power of 2 that is less than the or equal to the number as arguments.

binary-generator will take a number and power of 2 as input and will return a binary sequence of numbers as output. If the power of 2 is less than or equal to the number, it will invoke “word” with the following arguments: the digit “1” and a recursive call with the difference between the original number and the power of 2, and with 2^(n-1) power of 2. If the number is greater than the power of 2, then the procedure will return “0” and recursively call itself, not decreasing the number but decreasing the power by 1. This will continue until the power of 2 reaches negative 1, at which point the procedure should return "".

The result:

I treat 0 as a special case cuz I got errors resulting from log2 otherwise. Having 1 special case seems ok.

Whew, that was a lot of work! 😅

Other People’s Solutions

So it turns out this is way more complicated than it needs to be!

AnneB’s Solution

So let’s see how this works.

If we give it say 9, it will get remainder 9 2, which is 1, and then put the 1 as the second argument to a call to word. The first argument is a recursive call to to-binary with quotient 9 2, which is 4.

The recursive calls generate 0 a couple of times since remainder 4 2 and remainder 2 2, respectively, are both 0. Then when we get down to remainder 1 2, we get the final 1, and then the final recursive call returns a “”. So yeah I think I see how this works.

buntine’s Solution

buntine’s solution is more complex than AnneB’s but simpler than mine:

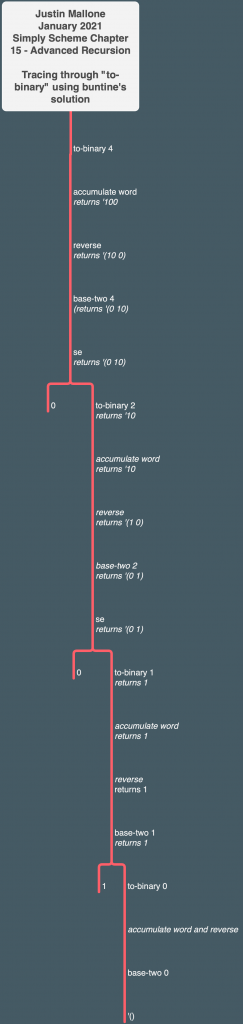
buntine’s base-two procedure plugs a number into remainder (floor n) 2 and checks whether that returns greater than 0. E.g. for 9, remainder (floor 9) 2) returns 1. OTOH, for 4, as in remainder (floor 4) 2), the value returned is 0. If the value returned is greater than 0, 1 is returned as an argument to se. Otherwise, 0 is returned. There is also a recursive call to to-binary with n divided by 2.

The way the program works is pretty interesting. to-binary is accumulating and reversing the values at each stage so the output comes out right. Without the reverse happening at each stage (so if to-binary was just accumulating word) the binary numbers would come out backwards.

Oh but hang on a second, I have an idea:

I improved it 😀

I put the recursive call first within base-two and got rid of the reverse. Hurrah!

Here’s a tree I made of buntine’s original version to understand how it worked:

pongsh’s solution

pongsh’s solution:

This is pretty similar to the last one in some ways but more elegant. It’s got the recursive call with (to-binary (/ (floor n) 2)) and is generating the 1 or 0 to use for a given number using modulo num 2.

✅ Exercise 15.2

A “palindrome” is a sentence that reads the same backward as forward. Write a predicate palindrome? that takes a sentence as argument and decides whether it is a palindrome. For example:

Do not reverse any words or sentences in your solution.

Here’s my solution. I’m using accumulate since they didn’t put any restrictions on the solution method besides not using reverse.

The only semi-tricky part was realizing that I had to turn the result of accumulate word sent into a word in order for my helper procedure to operate on it correctly. UPDATE: AnneB pointed out that this doesn’t actually make sense so I struck it out and updated/simplified my procedure accordingly.

✅ Exercise 15.3

Write a procedure substrings that takes a word as its argument. It should return a sentence containing all of the substrings of the argument. A substring is a subset whose letters come consecutively in the original word. For example, the word bat is a subset, but not a substring, of brat.

First Solution, Using Remdup

My solution, which uses remdup from exercise 14.3:

The tree I made earlier when I was trying to understand subsets is actually relevant:

This has duplicates (e.g. “ra” and various single letters). We don’t want those, so we use remdup to clean things up.

This is probably more computationally expensive than it needs to be, and maybe there is a better way to do it. It was very easy for me to understand and figure out though (it probably helped that I accidentally partly figured out this program while trying to deal with subsets earlier).

Attempting Another Solution

After working through the first exercise with the help of curi and Anne’s advice, and then glancing briefly at some other solutions and seeing that they looked very different, I thought I’d try coming up with another solution to this problem.

The procedure should take a word as an argument. It should figure out the length of the word, and then go through the word N–sized chunks at a time, from left to right, where N starts with the value of the length of the word and then decreases by one with each successive pass. The results of this passing through the word in and size chunks it should be grouped together into a sentence, and the passing through the word should continue until N reaches zero.

Since substrings is only supposed to take the word itself, the bulk of the operational work of the procedure will take place within a helper procedure.

There are a couple of sub problems that need to be solved in order for the procedure to work in the way that I’ve described. The first problem is that we need someway to only select a specific range of characters. The second some problem is that we need someway to pass through the word from left to right and then stop when we reach The point at which where as far right as we can go within the word while still having the number of characters that we need in that particular pass through the word.

Some notes: the amount of spaces that you need to scroll through the word is the same as the difference between the length of the original word and the current chunk size.

The number of chunks at a particular level increases by one as the chunk size goes down by one.

I tried making a very manual version of the program I was envisioning to see what it was like, specifically handling a case of four-letter input:

I had some difficulty seeing how I’d generalize this, so I started to wonder if I should take a new approach.

I persisted, and after some thinking and testing, managed to come up with this solution which worked but not in the way I wanted:

I want to note that it was at the stage of writing my detailed explanation of what each step of the procedure does (and reviewing the output from running trace in the course of doing so) that I realized that the procedure was operating differently than I intended. So I had a major misconception about how my procedure worked despite 1) having written down what I was trying to accomplish beforehand and 2) having output which made it looked like I’d solved the problem! 🤯 I thought this was notable – how I could have a misconception like this and only catch it at a fairly late stage. Better than not catching it at all 🙂

Second Solution

After some thinking and figuring out what was going wrong, I came up with this:

substrings itself invokes substring-helper with the wd and the count wd as arguments.

substring-helper is a fairly straightforward recursive procedure. If chunksize (the size of the chunks we want in the current procedure) is 0, we return the empty sentence. Otherwise, we invoke sentence with a call to the chunk procedure and a recursive call to substring-helper as arguments. The recursive call to substring-helper reduces the chunksize by 1.

chunk is where the interesting action in this procedure happens. The chunk procedure, in addition to having arguments for wd and chunksize, also has an argument for place. The place argument represents the number of digits between the start of the word and the beginning of the chunk in the current “pass” through the word. That’s why the call to chunk from within substring-helper starts place at 0 – we start gathering our chunks at the beginning of the word, and then with each recursive call to chunk we increase place by 1, and that moves the beginning of the next chunk over “one to the right”, and so on, until we’ve gotten each substring of a particular length. So the recursive calls to chunk generate the chunks for a particular length (say, 2 word chunks in a 4 letter word) and then substring-helper is responsible for making that all the lengths get generated.

This line…

…ensures that the chunk procedure stops and return the empty sentence when the combination of chunk and place exceed the size of the word. This is to ensure that the procedure doesn’t try to go “off the word” in collecting chunks, which would lead to an error. E.g. if you’re collecting two word chunks on the word “chat”, for the first chunk you’ll get “ch” when the place value is 0, and for the second chunk you’ll get “ha” when the place value is 1, and for the final chunk you’ll get “at” when the place value is 2. At this point, the sum of the place value and the chunk size is 4, which is the same as the word. If the program kept continuing on past this point, then it would try to grab a 2 letter chunk starting at the “t” of chat and at that point would hit an error.

I use repeated bf with the place value to actually move the “starting place” from left to right through the word. I also made a procedure, charsel, to actually select the characters. It takes a segment of the word (adjusted for starting place) and the chunksize as arguments and then selects the first character of the word while recursively calling itself and reducing the counter by 1.

Here’s the chunk part of my procedure in action with trace chunk provided the output in light purple:

Other People’s Solutions

AnneB’s Solution

Let’s walk through this.

For substrings, if count w equals 1, then sentence is invoked on w. Otherwise, substrings-helper is called with the first and second letters of word and another call to substrings as arguments. The other call to substrings is given butfirst w as its argument.

For substrings-helper, if sent (a call to substrings-helper) is empty, then a sentence is returned with f.

If the first letter of the first word of sent is equal to s, then a sentence is returned with first sent and a word made of f and first sent, and also, within that sentence being returned, there is a recursive call to substrings-helper.

Otherwise, a sentence is returned with first sent and a recursive call to substrings-helper. So the word made form f and first sent is missing.

I am finding the mechanics here a bit hard to follow. Let’s see what the trace looks like for “rat” as the input word:

While I have a vague idea of what’s going on, I’m still finding the details a bit difficult to follow, so I’m going to set this aside for now.

buntine’s Solution

This one I found easier to understand.

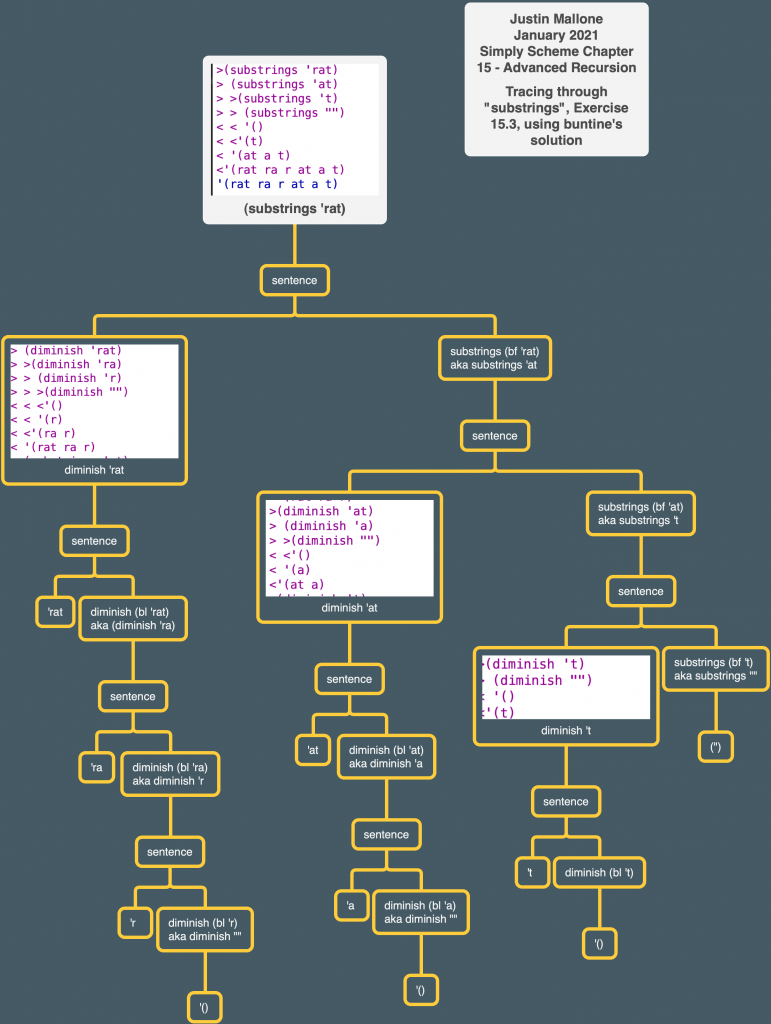
diminish takes a word and returns that word and does bl through the word, return the word at each step (e.g. for input word rat diminish will return rat, ra, r.) When the word is empty diminish returns the empty sentence.

substrings puts the results from diminish in a sentence and then recursively calls substrings with the bf of the word, which creates a new chain of calls to diminish for each bf of the word. So for rat, the procedure will first generate the rat ra r result like I said, and then diminish winds up getting run on at, which generates at a, and so on. By this method it goes through each substring of the word and does so only once. By the way, if you don’t want the empty word as output, it seems like you can change the se "" line to se '() with no negative consequences.

I made a tree to help me understand this one and found it helpful. By the way, MindNode users, if you have an image in your copy-paste buffer, you can paste it directly into a node by selecting the node and hitting cmd-v (on macOS).

✅ Exercise 15.4

Write a predicate procedure substring? that takes two words as arguments and returns #t if and only if the first word is a substring of the second. (See Exercise 15.3 for the definition of a substring.)
Be careful about cases in which you encounter a “false start,” like this:

and also about subsets that don’t appear as consecutive letters in the second word:

Trivial Solution

Here’s a trivial solution assuming you’ve solved 15.3 correctly:

First Attempt at a Non-Trivial Solution (failed)

Here was my first idea for a more complicated solution:

1. Check the letter of the first word against the first letter of the second word. If it matches, recursively call the checking procedure with the bf of both words.
2. If the first word becomes empty before you run out of characters in the second word, return #t.
3. If the second word runs out of characters before the first, return #f
4. Otherwise, recursively call the checking procedure with the original word as the word you are checking (“resetting” the word you are checking to the original word after a failure to find a match) and with bf of the second word.

This did not work. It ran into one of the problems from the book examples. See the image below for the line that indicates the problem:

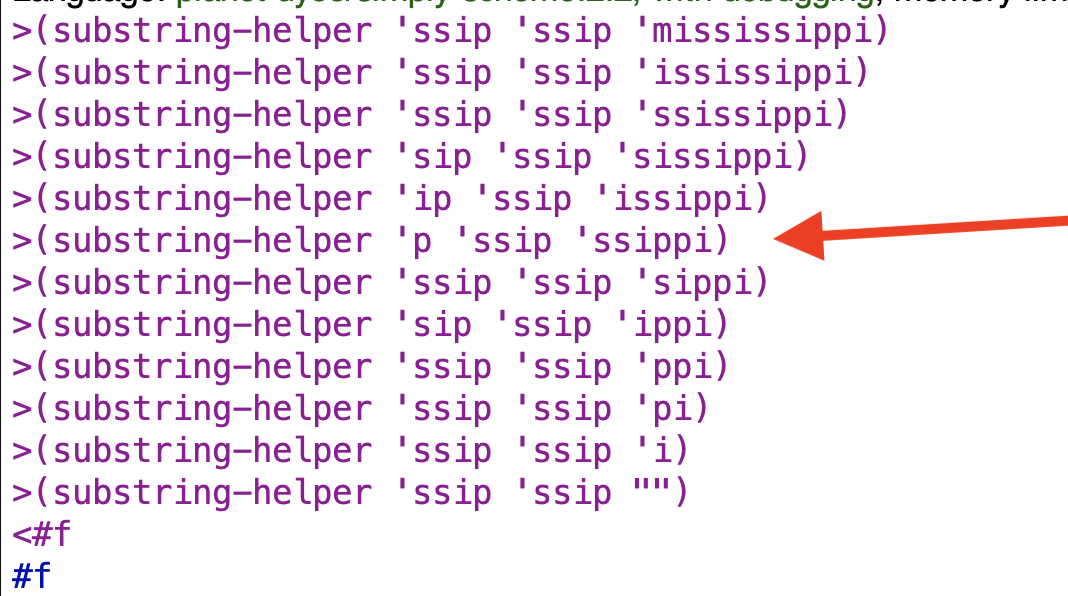
The problem is that currsub doesn’t reset soon enough after the “false start” of mississippi and so misses the match for ssip.

Second Attempt at a Non-Trivial Solution (Success)

I decided to try a different approach incorporation one of the helper procedures from my previous solution in 15.3. The basic idea is this: generate subsegments of the second word equal in length to the substring (the first word) you’re trying to find a match for. If no match is found, do the same process but on bf of the second word. Keep going until you find a match (in which case you return true) or the length of the first word exceeds the length of the second (at which point a match becomes impossible and you should return false).

The implementation:

You can see the difference in operation below:

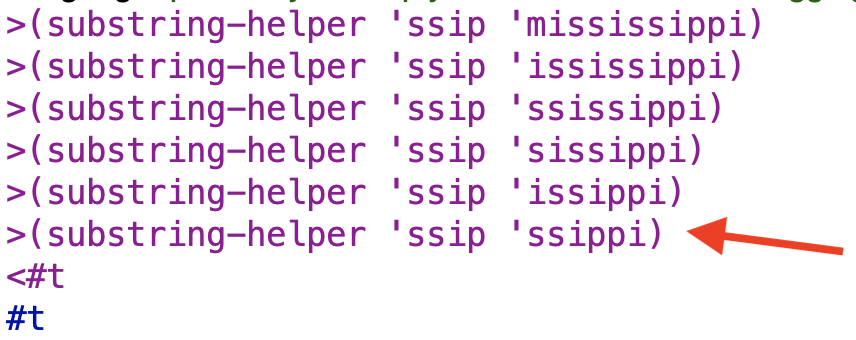
the same sub is being tested against the first four letters of the ever-shortening second word each time, so ultimately we get a true result.

✅ Exercise 15.5

Suppose you have a phone number, such as 223-5766, and you’d like to figure out a clever way to spell it in letters for your friends to remember. Each digit corresponds to three possible letters. For example, the digit 2 corresponds to the letters A, B, and C. Write a procedure that takes a number as argument and returns a sentence of all the possible spellings:

(We’re not showing you all 2187 words in this sentence.) You may assume there are no zeros or ones in the number, since those don’t have letters.
Hint: This problem has a lot in common with the subsets example.

Already so suppose we just gave it “2”. We’d want it to return A, B, and C.

This very minimal procedure gets us that far, but obviously we want way more functionality 🙂

If we just add a line in phone-letters for the 3 digit, we get this result:

If we want to get to the point of handling 2-digit numbers, we need to have some sort of way of prepending things like the book people did in subsets.

So what we want is to get say the letters for 2, '(a b c).“, and the letters for 3, (d e f). And then we want to return a sentence that’s like:

(ad ae af bd be bf cd ce cf).

So what’s this sentence made out of?

It goes through each value of the (a b c) sentence and prepends it to the values for the (d e f) sentence. So first it prepends a to each element of (d e f), and then does the same with b and c.

So we’ll need some way to take two sentences and generate such a list. The following procedure accomplishes that goal by building on prepend-every.

Let’s try using it:

Hmm. So we’re getting there but there are two problems:

1. We don’t want the single digit values
2. We don’t want the empty word

I reorganized my program a bit and added a couple of helper procedures and a keep:

atleast takes some word (such as the initial numeric sequence) as an argument and returns a procedure that checks whether a value provided by a higher order procedure is at least as long as the input to atleast. In combination with keep, it ensures that any values that are kept from the sentence that results from running phone-speller-helper are at least as long as the original input number.

Here’s the full, completed program:

I ran this:

…and get a different result than the book’s 2187; instead I get 2916. I think the book people are using a different set of mappings of digits to letters for whatever their equivalent of phone-letters is. I initially got 2187 but then added a letter to the sentence for digit 7 that was missing and I got the 2916 that other solutions got.

Other People’s Solutions

AnneB

AnneB’s solution.

Let’s go through it. prepend-letter and prepend-letters are pretty similar to my prepend-every and prepend-sentence. phone-spell is notably different though:

So the base case is if the count of phone-number equals 1. You have to cut it off before the count gets to 0 or else you’ll get errors when trying to use item. In that case, a sentence is accumulated out of the letters in phone-letters that match that single number. For example, for the number 3 you get '(g h i)

If the count of phone-number is greater than 1, prepend-letters is invoked with (prepend-letters (item (first phone-number) (phone-letters)) (phone-spell (butfirst phone-number))))).
Here’s an example trace of running prepend-letters:

In this manner all the relevant letter sequences are generated.
I made a tree in order to understand how Anne solved her version. That tree is below:

I should have used item for phone-letters like AnneB did. I’ve used item for similar purposes before but defaulted back to a big cond here.

✅ Exercise 15.6

Let’s say a gladiator kills a roach. If we want to talk about the roach, we say “the roach the gladiator killed.” But if we want to talk about the gladiator, we say “the gladiator that killed the roach.”
People are pretty good at understanding even rather long sentences as long as they’re straightforward: “This is the farmer who kept the cock that waked the priest that married the man that kissed the maiden that milked the cow that tossed the dog that worried the cat that killed the rat that ate the malt that lay in the house that Jack built.” But even a short nested sentence is confusing: “This is the rat the cat the dog worried killed.” Which rat was that?
Write a procedure unscramble that takes a nested sentence as argument and returns a straightforward sentence about the same cast of characters:

You may assume that the argument has exactly the structure of these examples, with no special cases like “that lay in the house” or “that Jack built.”

Attempting the Solution

This is sort of getting towards the right output but not quite:

Already let’s try talking this out in English with the gladiator/roach case.

input:

I want to get to this:

So the gladiator is VERBing the first thing.

I think the basic structure we want is this: if a sentence starts with “this is”, we grab the first thing after the “this is” (here, “the roach”) and put it at the end, and then we recursively call unscramble without the first thing.

Hey we’re starting to get close!

And then if a sentence doesn’t start with “this is”, but instead starts with “the”, we take the first two words + 'that plus the last word, put that on the end, and then do another recursive call to unscramble with like (bl (bf (bf sent)))).

ah-ha!

😀

Full Solution

Full program. I changed the base case to (= (count sent) 0) cuz I didn’t see a need to include the case where sent = 1. I think the reason is that since we’re assuming all the input will be in a certain format, we’ll always wind up with 0. “this is the x” is a 4 word chunk which my first recursive case addressed, and the other cases are all “the x” + a verb, which is a 3 word chunk my second case addresses. All properly formatted input sentences will be some combination of a 4 word chunk plus a group of 3 word chunks (e.g. “this is the roach” + “the gladiator killed”, or “this is the rat” plus “the cat … bit” and “the dog…chased” and so on). So we’ll always get to 0, so that’s the only case I need to worry about.

Other People’s Solutions

AnneB broke out dealing with the middle of the sentence into a separate procedure rather than dealing with it all in one procedure. I think that organization is better. She also assumed the formatting of the sentence rather than testing. I think that makes sense.

buntine did a totally different approach, where he appears to have extracted the elements of the sentence and reassembled them. I haven’t looked in detail at it but I liked the general idea. Note his procedure is mislabeled: by nouns he actually means verbs.