Simply Scheme Project: Spelling Names of Huge Numbers

Write a procedure number-name that takes a positive integer argument and returns a sentence containing that number spelled out in words:

There are some special cases you will need to consider:
• Numbers in which some particular digit is zero
• Numbers like 1,000,529 in which an entire group of three digits is zero.
• Numbers in the teens.

Here are two hints. First, split the number into groups of three digits, going from right to left. Also, use the sentence

You can write this bottom-up or top-down. To work bottom-up, pick a subtask and get that working before you tackle the overall structure of the problem. For example, write a procedure that returns the word FIFTEEN given the argument 15.
To work top-down, start by writing number-name, freely assuming the existence of whatever helper procedures you like. You can begin debugging by writing stub procedures that fit into the overall program but don’t really do their job correctly. For example, as an intermediate stage you might end up with a program that works like this:

Solution

I solved this by first mostly solving the problem for 0 through 999, then testing and adding more stuff on.

Harder Sub-procedures

Here I’ll talk about the procedures I thought were harder/more difficult to figure out for solving this problem.

---

Here’s what I wrote for number-name:

So big picture the main program does a couple of things:
1) checks for a few special cases,
2) hands off the number to helper procedures for further processing if appropriate.

the ((not (number? number)) and ((not (integer? number)) cond lines check to see if the input is not a number or not an integer, respectively, and return an appropriate message if that is the case.

((equal? number 0) '(zero)) checks if the number is equal to zero. Note that this will return true for stuff like -0 or 00000, so you don’t have to check for those cases specifically – Scheme handles all that. If the test returns true, a sentence with the word (zero) gets returned. I made it a sentence in order to have it be consistent with other program outut.

This part of the program first checks if a number is negative. If so, invokes sentence with the word “negative” and then calls number-name-helper in much the same way that the else line does, with the caveat that invokes triple-number-accumulator with (bf number) instead of number in order to “skip over” the negative number that has now been addressed.

The else calls a helper procedure number-name-helper with two arguments: the result of invoking triple-number-accumulator with number, which generates a sentence with the number broken up into sets of three numbers, and 0. The 0 represents the initial value for large-number-count, which is the value that I use to keep track of what large number name to use (thousands, millions etc).

---

This part is a procedure that does some important stuff.

First lets consider the arguments. triple-sent is the sentence consisting of words of up to three digits (which I’m thinking of as “triples”) generated by calling triple-number-accumulator. I say “up to three digits” because, depending on the input number, some words will be shorter. Here’s what the output for triple-number-accumulator looks like for “12120301912607891”:

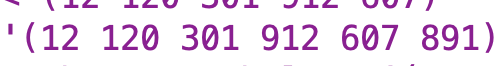
large-number-count is a counter I use to keep track of what large number name to use.

((empty? triple-sent) '())

The base case for the number-name-helper procedure is when triple-sent is empty. This happens when all the triples in triple-sent have been dealt with.

The recursive case does four important things:

1. (number-name-helper (bl triple-sent) (+ large-number-count 1))
   It invokes number-name-helper recursively on bl triple-sent. It’s bl triple-sent because the rest of this procedure will process last triple-sent into words, and because I’m dealing with triple-sent from “right to left” as the book suggested. It also increases large-number-count by 1. This will allow my program to pin the correct name on procedure if it involves big numbers.
2. (triple-helper (last triple-sent))
   It invokes triple-helper on last triple-sent. triple-helper is the procedure that has the core of the logic of how to deal with the three number sequences outputted by triple-number-accumulator and turn them into words.
3. 
   This line of the procedure checks if the current three-digit word (“triple”) is equal to "000". If the triple is not equal to "000", then this line invokes large-number-name with large-number-count. If the triple is equal to "000", then this line returns '(), effectively “skipping over” invoking the large number value for this part of the number.
   This was one of the trickiest parts for me to figure out and only got fully addressed in testing. Initially I just had a straightforward invocation of large-number-name with large-number-count. That worked in many cases, but if you had three digits that were all zeros, you could wind up with something like “one million thousand” as output for 1000000. That is obviously wrong. So I realized that I had to make the invocation of large-number-name conditional on the value of the triple not being “000”. What I did not realize, and what took me sometime to figure out, was that for some reason, Scheme was having my triple-accumulator procedure output quote marks around sets of three numbers where there are 0’s on both sides. Here’s a sentence of triples showing what I mean:
   
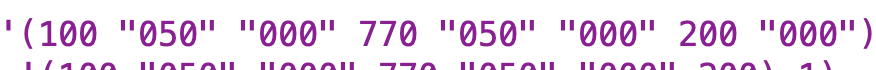
   I initially did something like (if (not (equal? (last triple-sent) 000)) expecting that to work (in fact, cuz Scheme generally treats 0 and 000 and 00000 and -0 as equivalent expressions, I should have been able to just do (if (not (equal? (last triple-sent) 0)) and have that work). I didn’t realize that the quote marks around “000” were absolutely critical for the procedure to function properly.

4. It combines the results of the three previous steps with sentence.

---

The first two lines of this procedure are important for handling 0’s within a 3 digit sequence.

If a three digit sequence such as “307” is passed to triple-helper, the ((equal? (first number) 0) (triple-helper (bf number))) line tells the procedure to “skip” past the “0” so that the rest of the number can be processed. Here’s a trace using this example:

((empty? number) '()) helps deal with the case where a three digit number ends with a zero. Without ((empty? number) '()), the procedure would try to use ((equal? (first number) 0) (triple-helper (bf number))) and would bf number on an empty word, giving an error. ((empty? number) '()) allows the procedure to handle this situation gracefully:

It can also handle stuff like “000” on the same principles.

This line handles triple-digit numbers greater than 100. It uses a single-digits helper procedure + 'hundred' to generate the name of the hundreds’ place, and then recursively calls triple-helper without the hundreds place in order to generate the rest of the name of the triple.

This line handles the names of the numbers in the tens place for numbers at least equal to 20. It uses a tens-place helper procedure to generate the name, then recursively calls triple-helper without the tens place in order to generate the rest of the name of the triple.

This line handles the names of numbers from 10 to 19. It does not recursively call triple-helper because of how number names work in English (e.g. for “22” you can make that out of “twenty” for the tens place plus “two” for the ones place, but for “12” there’s a name, “twelve”, that conveys what the values are in both the tens place and the ones place).

This line handles 1 through 9 using single-digits.

---

This procedure is the procedure that takes a number and makes a sentence of at-most three digit words for further handling by the overall program.

The base case: if the number of digits in the number is less than or equal to 3, those digits are returned as a sentence. sentence is invoked here for consistency of output for cases when only a three digit number is passed into the procedure.

The recursive case: triple-number-accumulator is called recursively, excluding the last three digits of number. Those digits are combined into a word. The results of the recursive call and the word-formation are combined into a sentence.

If we were start from the beginning of the number (left to right), we’d have to figure out what the groupings of the three digits should be based on the sentence, or else we might wind up with erroneous groupings like (123 456 789 0) for 1,234,567,890 when what we want is (1 234 567 890). But by starting from the end of the number, we can just “grab” groups of three numbers freely until we run out of those, and then “grab” whatever numbers are left at the end.

Easier Sub-procedures

These are the sub-procedures I think are more straightforward.

If large-number-count is greater than 0, the value of large-number-count is used as an argument to item to pull the appropriate word from the sentence of large number names provided by the book. Otherwise (meaning when we’re dealing with only three digit numbers) the empty sentence is returned.

---

These procedures all operate on the same principle, which is to use item and then a number value to pull a particular name of a word from a sentence. single-digits is the most straightforward, since the number provided to item and the name of the number are the same – meaning that 1 as a number gets you “one”, 2 gets you “two” and so on.

With tens-place, because I started my sentence with “twenty”, “twenty” is the first value of the sentence. When I want to grab the word “twenty”, it will be when the number in the tens place is 2. If I want to grab the first word of a sentence using item when number is a 2, I have to subtract 1 from 2 so that the number becomes 1 and will therefore retrieve the first word when passed as an argument to item. The same principle applies to the other numbers in the sentence (meaning that if I want to get “thirty” when the number in the tens place is 3 and “thirty” is the second word in the sentence, then I need to subtract 1 from 3).

The same idea from tens-place about “offsetting” number by a value so that it corresponds to the word within the sentence you want to select applies to tens (which should have maybe been named teens although that’s not quite accurate either). In this case, the incoming numbers will range from 10 to 19, and this corresponds to the words in the sentence which range from “ten” to “nineteen”. In order to make it so that the number 10 gets the first word of the sentence “ten” (and to have all the other number values select their appropriate words), we subtract by 9.

I think this organization of the program makes sense because

---

Pretty self-explanatory I think.

Full Program

Tests

Other Solutions

AnneB

AnneB made a diagram, which I think is good. I managed to intuitively “feel” my way through coding the whole procedure but that’s a very unreliable method for me.

If a number has fewer than four digits, AnneB sends the number straight to the group-name procedure. Otherwise, the results of calling a helper procedure with all but the last three numbers and group-name with the last three numbers are sentence‘ed together.

AnneB doesn’t appear to break up the number into a sentence of three-digit words right off the bat like I do. Instead she breaks up the word into three digit chunks as she goes along with calls (including recursive calls) to her number-name-helper and with the use of her helper procedures last-three and all-but-last-three. Also of note is that she passes in group-words as one of the arguments to number-name-helper. group-words is basically just the name of the sentence of large number names:

So AnneB will be using this sentence directly rather than my more indirect method involving a counter and item.

There are a lot of similarities in the overall structures of our number-name-helper procedures, at least for the case where count n is at least 4. AnneB starts her helper procedure with a recursive call to itself with all but the last three numbers,. Since I already broke up the number into at-most three digit words within a sentence, I was able to just bl my recursive call, but AnneB took a different approach and used her all-but-last-three procedure to accomplish a similar task. She also does butfirst names, which queues up the next large number name (in group-words) as appropriate for the next recursive call. AnneB’s approach to the large number names avoids the necessity of having to use a counter – she just butfirsts through the sentence of large number names directly. I think this is more elegant than what I did.

AnneB then uses group-name, which is somewhat analogous to my triple-helper, on a three digit sequence of numbers.

AnneB deals with the “three zeros” problem next. If the last three numbers of the number are 0, the empty sentence is returned, skipping over the large number name (e.g. thousands, millions) for that three digit sequence. Otherwise, the first of names (group-words) is returned.

Note that had to add some quote marks around multiple 0’s in some spots to get Anne’s code to run, and those changes are reflected in my pastes of her code.

I made a tree which illustrates some of the similarities in the number-name-helper procedures:

group-name appears to be somewhat similar to my triple-helper, in that it’s the program that handles sets of three numbers and passes them off to helper procedures that actually generate the file number names. We handle hundreds somewhat differently – my procedure checks if a number is greater than or equal to 100 and then forms the number name for the hundreds’ place using the single-digits helper procedure & the word 'hundred, and, if so, then recursively calls triple-helper to get the rest of the name of the number. Recursive calls to triple-helper actually occur in my triple-helper procedure for any number greater than 19. AnneB’s procedure checks if a number has three digits and, if so, then calls a hundred-name helper procedure and a two-digit-name helper procedure. Otherwise two-digit-name gets called. So the procedures have somewhat different “flow” and my triple-helper procedure does a lot more work. It occurs to me that maybe it does too much work and that Anne’s is better organized.

One other detail item I wanted to comment on is that Anne used item to pull out a specific desired word within a sentence of number words, but did so in a slightly different way than I did. I put the item invocation within a procedure that contained the sentence of number words, as in my version of single-digits, which I consider a “lower level” procedure because it doesn’t refer to any other procedures besides Scheme primitives. OTOH, Anne did stuff like this:

Note that the item is on the side of the “higher level” procedure and not the “lower level” procedure. And likewise AnneB handled “offsets” (like needing to subtract 1 for her tens-words, which was the equivalent of my tens-place) on the side of the higher level procedure. I don’t have a strong opinion on which approach is better, if any. I noticed the difference and it seemed interesting, because there is a structure choice there that I hadn’t really thought about (just followed my intuitions).

Big picture comment: unlike my number-name procedure, AnneB’s procedure does not appear to handle negative numbers or numbers with leading zeros like 00010000. For numbers equal to zero, I get the empty sentence as a result instead of '(zero) as in mine. It also doesn’t handle non-integers or non-numbers.

buntine

buntine’s solution seemed interesting. Want to go over one thing in detail:

Let’s go one step at a time:

Let tr be defined as a function of two arguments, i, and f. If i equals 0, return the empty sentence. Otherwise, let i be an argument to the function f.

If n is true for teen?, return teen n, otherwise return the following big cond.

Note the structure btw: we’re testing for the teen? special case up front and then looking at other stuff if the number doesn’t return true for teen?

first line of the cond that’s serving as the alternative to our if. This is where we get into using tr.

So by the logic of our let and of how let works, we can say the following: if n has 1 digit, and that digit is 0, then this will return the empty sentence. If n has one digit that is not 0, however, then ones (which is the procedure buntine uses to translate single digits into words) will be invoked with n as the argument.

If n has 2 digits, check if it’s a teen number and return teen n if so. Otherwise, return the appropriate number name in words by invoking sentence with the arguments tr (first n) tens) (which will get the appropriate tens-place name – e.g. twenty, thirty, whatever) and tr (last n) ones which will get the appropriate single digit name.

🤔 🤔 🤔 🤔 🤔 🤔 🤔 🤔 🤔
Since we already checked for teen? before getting to the cond, I’m unclear why it’s necessary to do so again.

This is the big else statement of the cond. This handles hundreds.

The (tr (first n) hundreds) handles the hundreds place, pretty straightforward.

The (if (teen? (last-n n 2)) (teen (last-n n 2)) line is more interesting. last-n is a nifty procedure that lets you arbitrarily select the last n characters in a word (or number) by repeatedly calling bf a number of times equal to the difference between the count of the word and n:

So e.g. last-n 'potato 4 will call bf (- 6 4) or 2 times, giving us tato. buntine uses this procedure to select the last two digits within the n in the case of a number in the teen range.

The alternative to the if condition is that the tens and ones procedures are respectively invoked on the appropriate number. I think the fact that tr returns an empty sentence in the case of a 0 helps deal with 0’s in numbers.

Here’s a tree of buntine’s translate n procedure:

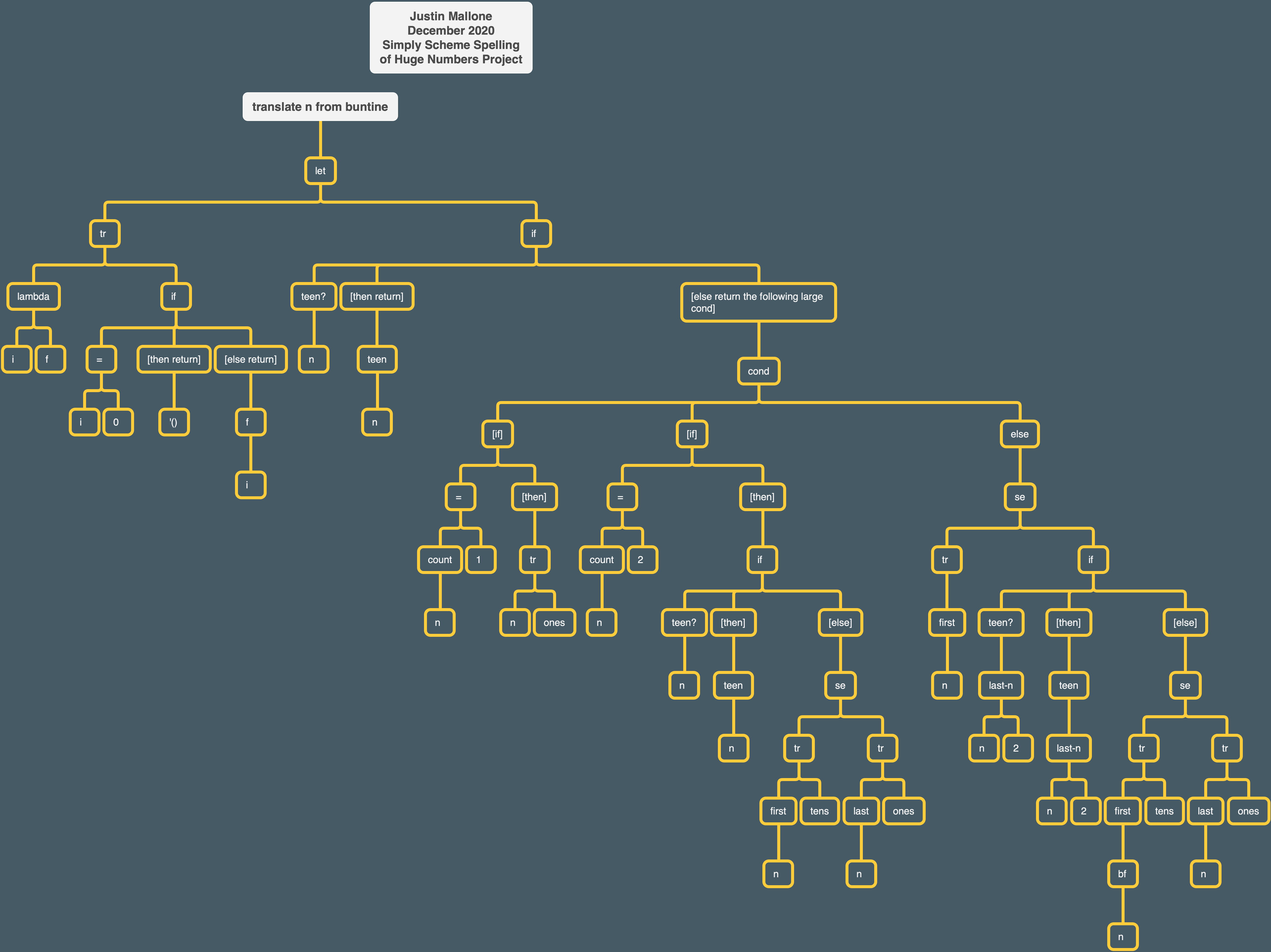
buntine’s overall number-name procedure can’t handle negative numbers, non-numeric input, or decimals. It can, however, handle leading zeros.