I’ve done some exercises in Simply Scheme a couple times previously. I figured I would try to go through it in a more thorough, careful and documented way while keeping in mind the lessons I learned from my recent Peikoff Grammar Course project. My work will be posted at a Github repository.

Goals

1. Practice overall learning methodology stuff like writing thorough explanations, brainstorming, using trees, and going step by step.
2. Review previous learning efforts of mine, along with other people’s learning efforts, and compare and contrast, reflecting on differences, mistakes I made, things I can do better, etc.
3. Gain some subject-matter specific knowledge I can build on for later learning efforts and ultimately for some specific projects that I’d like to work on.
4. Avoid getting stuck, and work on quickly and successfully getting unstuck if I do get stuck.

Avoiding Getting Stuck

Avoiding getting stuck warrants some more discussion, since that’s been a big issue for me in prior learning efforts.

I found the general principle described in this article of Elliot’s to be quite helpful. I don’t think I’ve perfectly applied it, but it’s something my mind turns to when I really feel like I’m stuck and spinning my wheels.

Another thing that’s helped with getting unstuck is paying attention to how much I am writing. As a rough approximation, if I am regularly writing something while working on stuff, things are going okay. In the worst case, if I am writing stuff and I have a misconception, then I am providing more detail about my misconceptions and so am making it easy for either myself or others to see the misconceptions. And if I am actually on the right track, then writing means I’m working my way (however slowly) towards some sort of conceptual clarity. I think some sort of measure or indicator of making progress like this is important. It’s not perfect, but if you notice that your word count hasn’t moved for a while, that’s at least a potential alarm bell to indicate to you that something is going wrong. So between paying attention to amount of time I’ve spent thinking about something, and paying attention to how many words I’ve written, that’s two potential alarm bells I have for the issue of getting stuck.

I think the getting stuck issue has an aspect to it that involves a misconception around what problem solving is supposed to be like. I think of it as a sort of romantic misconception (in the broader and the sexual/relationship sense of that term) where the solution to a problem comes to you in a sudden flash of inspiration. This is connected with certain ideas people have about genius. I think the truth is that a lot of what people consider genius consists of having certain traits in a thorough way. Some traits that I think are important:
– being organized and systematic in what you do.
– being honest about what you know and don’t know
– seeking out and being open to criticism about what you are doing.
– being intellectually curious about what you are working on.
There are also bad traits you need to avoid, like being disorganized, dishonest, hostile to criticism, and passive.

Getting DrRacket Set Up

Before doing anything else, I need to get DrRacket set up on my Mac, and figure out how to load a definitions file that will let me do the exercises effectively. I already DrRacket installed, so the main thing was loading a definitions file.This file from github seems to do the job. I googled for the appropriate way to get started and tried a few different things. Initially, I was trying to use the definitions file from github and getting an error message about a bad relative path in DrRacket. I figured out that the file paths seem to be relative around the current file I am working in. I made a test file called “test.rkt”, made a subdirectory called “definitions” (since the file from github defines a bunch of procedures) and put the file from github into it. In test.rkt, I entered the following into the definitions window (which is the top part of the interface)

I then ran this, and:

🙂

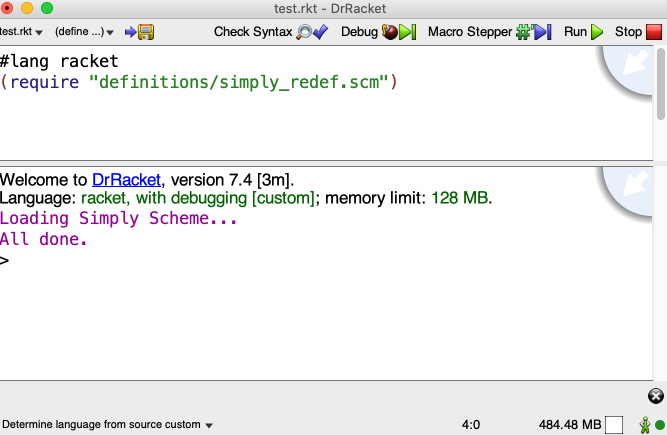
Testing a Simply Scheme procedure:

Hmm. I think the output is not supposed to have an apostrophe like that, based on this chapter: https://people.eecs.berkeley.edu/~bh/ssch5/words.html

I tried a couple of Simply Scheme packages available for download through the DrRacket manager and they had similar behavior as far as apostrophe. I think I won’t worry about the apostrophe for now unless it causes an issue. I’ll use the github simply scheme file for now.

Quotes in a given section come from the chapter of Simply Scheme in question unless otherwise specified.

Some DrRacket macOS Keyboard Shortcuts

In the interactions window, esc + p for previous command entered, and hit esc + n for next command. Seems like you need to hit escape each time – you can’t just hold down escape and hit p or n to cycle through recent commands.

ctrl + left or right arrow to move forward or back a line, respectively.

esc-backspace to delete a word.

Getting Github Set Up

I made a Github repository for my Simply Scheme work.

I already had the Github Desktop App set up on my Mac. I just needed to make a New Repository for Simply Scheme and then put the files I’m making in that repository.

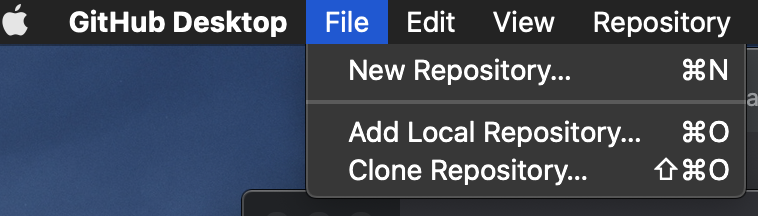
Github Desktop shows you changes that have been made to your files and which files have been changed.

You have to provide a brief summary of your changes before you can hit the Commit button.

And then you have to push the changes for them to get published to the web.

Using the Fallible Ideas List Discussion

There have been lots of posts on the Fallible Ideas list (mostly by AnneB) about Simply Scheme. I intend to refer to these as I work my way through the course. I set up a Smart Mailbox in MailMate to help me keep the relevant posts handy

Reviewing Past Work

Since I’ve tried working through this book previously, I will be referring to what I’ve done previously and comparing that to what I am doing now. I’ll do this at the end of each chapter.

Part I of Simply Scheme

Note that since I’ve gone through some of the course before, I know that sentences are lists, what some basic functions do, and various other details. So sometimes I may refer to things in light of context that I already have but that I may not have introduced in my notes.

Introduction: Functions

Our goal is not for you to feel that you could re-create these programs, but rather that you get a sense of what kinds of programs we’ll be working with.

Minor grammar issue here (I’m trying to actively notice things in order to keep my grammar skills sharp): this sentence should be “but rather [for] you [to] get a sense” to maintain parallelism.

Chapter 1 – Showing Off Scheme

Quotes in this section come from this chapter unless otherwise specified.

Procedure syntax – The parentheses are syntax for indicating to Scheme that we’re calling a procedure. The ' is important too (indicates string IIRC).

Primitive procedures: procedures Scheme already knows.

Compound procedures: procedures we define.

Example: Acronyms

I ran the following code on some example inputs:

So basically (starting from the inside and working my way out), (every first phrase)) applies first to every word of phrase, getting the first letter of each word in the phrase. accumulate word accumulates the letters produced by that process into a word. word tells accumulate what to do – accumulate can do different things, like add up a bunch of numbers if you tell it to + or find the highest number in some list of numbers if you tell it to max.

Simply Scheme says:

Accumulate takes a procedure and a sentence as its arguments. It applies that procedure to two of the words of the sentence. Then it applies the procedure to the result we got back and another element of the sentence, and so on. It ends when it’s combined all the words of the sentence into a single result.

So every first phrase grabs the first letter of each word in the phrase. So suppose the phrase is (make america great again). every first phrase will spit out (m a g a) from that.

Then accumulate word puts the first two letters together, and then takes those first two letters and adds the third letter, and then takes the now three-letter word and adds the fourth letter.

I wanted to show what was going in detail in DrRacket. I ran into the issue that if you try to use trace on some things like word, it gives an error and won’t run. I got the idea from a stackoverflow comment that I could define an alias for the name of function I want to trace, use the alias in place of the original function, and run trace on that.

So by writing this

I was able to get this output:

So that follows what I expected re: how word operates, with the exception that it seems to be starting from the end of the phrase rather than the beginning.

The output was different between some examples in a way that I thought was interesting:

Note that the capitalization is respected and, more interestingly, that the output has “quotation” marks around it if any of the letters are capitalized.

It looks like capital has to be in one of the first letters of each word (the letters that make it into the acronym) for the output to get the quotes. Otherwise, the output just goes back to the apostrophe. I’m not sure why the output has this variation.

Did you have trouble figuring out what all the pieces do in the acronym procedure?

I think that the procedure goes through each word in a list of words that you pass it, and then takes the first letter of each word one and builds a new word out of that, and that becomes the acronym.

Notice that this simple acronym program doesn’t always do exactly what you might expect:

I expected it to do that 🙂

So now I think that the program is checking each word against a list of words defined in (real-word?). The list of words includes some articles and prepositions that we want to treat as not being real words for the purpose of making acronyms. I think (real-word?) works by checking that a word is not a member of the list of not-real worlds. If a word is not a member of the list, it gets included in the acronym. If it is a member, it doesn’t. I forget a lot of details about the exact step-by-step operation (which I expect to refresh myself on shortly) so this is just a high level summary of what’s happening.

Below is some output from running the updated version of the acronym program on some input:

So now it handles that preposition.

This shows that the real-word? function returns a boolean value.

Example: Pig Latin

The Simply Scheme text contains an important note about this expression:

(By the way, if you’ve used other programming languages before, don’t fall into the trap of thinking that each line of the pigl definition is a “statement” and that they are executed one after the other. That’s not how it works in Scheme. The entire thing is a single expression, and what counts is the grouping with parentheses. Starting a new line is no different from a space between words as far as Scheme is concerned. We could have defined pigl on one humongous line and it would mean the same thing. Also, Scheme doesn’t care about how we’ve indented the lines so that subexpressions line up under each other. We do that only to make the program more readable for human beings.)

This note contains some important points:
1) the whole pigl program is a single big expression, not something with different parts that exist on multiple lines.
2) for the purposes of scheme, new lines and spaces are treated the same.
3) scheme does not care about indentation.

The pigl program checks if the first letter of a word is a vowel. If it is, it appends “ay” at the end of the word and returns the word. If not, the program calls itself again on a word consisting of the current word but with the first letter moved to the end. (word (butfirst wd) (first wd)) is the part that moves the first letter to the end.

You’ve seen every before, in the acronym example, but we haven’t told you what it does. Try to guess what Scheme will respond when you type this:

(every pigl '(the ballad of john and yoko))

every applies a function that follows it to each word in a sentence. So every pigl will apply pigl to each word in the sentence above, producing something like ethay alladbay ofay ohnjay anday okoyay. Let’s check:

yep 🙂

Example: Ice Cream Choices

Ok now we’ve gotten to an example that I cannot easily describe the operation of offhand. I remember being a bit fuzzy about map and reduce in particular, and being confused about lambda as well.

Lambda

Chapter 9 describes lambda as

the name of a special form that generates procedures. It takes some information about the function you want to create as arguments and it returns the procedure.

The book says that if you want to add 3 to every number in a list using the tools the book teaches you before it introduces lambda, you have to do something like this:

Every needs a function to apply to stuff, so you need to give it a function. In the above example, you define a helper function “add-three” for the purpose of having a function to use with every.

It’s slightly annoying to have to define a helper procedure add-three just so we can use it as the argument to every. We’re never going to use that procedure again, but we still have to come up with a name for it. We’d like a general way to say “here’s the function I want you to use” without having to give the procedure a name. In other words, we want a general-purpose procedure-generating procedure!

So that’s what lambda is.

Creating a procedure by using lambda is very much like creating one with define, as we’ve done up to this point, except that we don’t specify a name. When we create a procedure with define, we have to indicate the procedure’s name, the names of its arguments (i.e., the formal parameters), and the expression that it computes (its body). With lambda we still provide the last two of these three components.

Here’s an example of lambda:

So a and b are the formal parameters, and then a function is defined which multiplies a by 2 and then takes that product and adds b to it, and then 5 and 6 are provided to the function, and so the result is ((2 x 5) + 6) or 16.

Structure of Programs

I wonder if it’s actually more than “slightly annoying” to have to define a helper procedure in this case. I wonder if breaking out tiny bits of programs you only use once is a bit like having too many commas.

If you don’t have any commas and just go on and on in a long continuous unbroken stream of thought then it becomes overwhelming and that’s too little structure.

On the other hand, if, you have, say, a constant stream, of breaks, in your thoughts, using commas, then, you render the commas, kinda useless, as a structuring device, by virtue, of your, overuse.

My naive guess is that parts of programs should be broken off into a separate part according to criteria like: reaching a certain level of complexity, getting repetitively used a certain amount, and other stuff. And so a part of a program that does a simple thing a grand total of one time is the poster child for what you don’t want to breaking off into a separate function. And so structuring a function in such a way would actually be bad, objectively.

Other Functions in the Example

Let

I got a little confused trying to figure out what let does and how it’s different than lambda. I don’t wanna get stuck in the mud by jumping the gun (intentional mixed metaphor 😉 ) so I won’t worry too much about this for now. It seems like let is kind of similar to lambda, except with lambda you don’t give the temporary function a name and with let you can (or have to? Not sure).

Map

map is similar to every. See this chapter. That chapter describes an important difference between map and every, which is that map preserves nested list structures while every flattens them. every applies a function that follows it to each word in a sentence. map applies a function that follows it to each item in a list.

Reduce

reduce is similar to the accumulate function used in the Acronyms example. Accumulate “takes a procedure and a sentence as its arguments. It applies that procedure to two of the words of the sentence.” Chapter 17 of Simply Scheme says that “Reduce is just like accumulate except that it works only on lists, not on words.”

Append

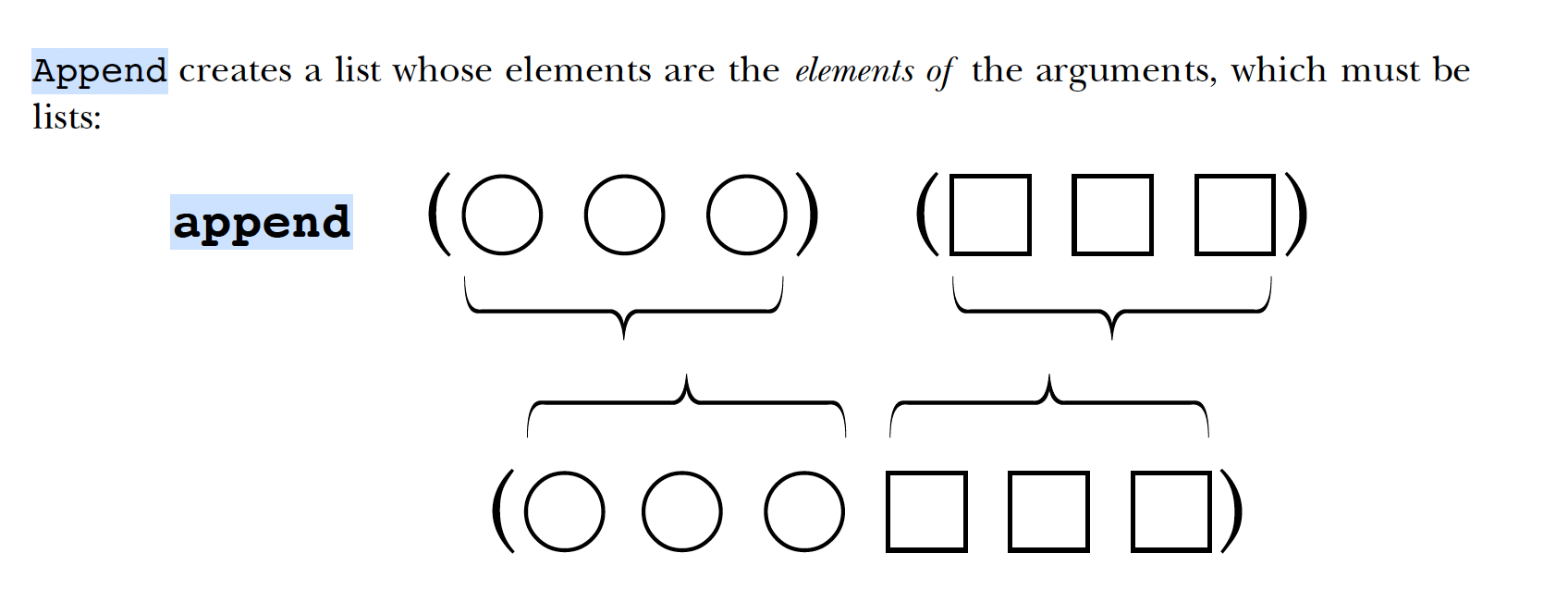
Append makes a list out of the elements of lists provided as arguments.

car & cdr

car selects the first element of a list, and cdr selects all but the first element. So they’re kind of like first and butfirst.

Looking at Ice Cream Choices Again

This part checks if the “menu” is empty and, if so, returns an empty list:

This let (I think) creates a function named “smaller” that callschoices on all but the first item in the menu:

I got pretty stuck trying to figure out what’s going on with the reduce/append/map/lambda part. It’s a lot of moving parts. I think I’ll just wait on that for now.

Running the Example

If you run the choices program with the following input:

you get:

huzzah 🍦

Example: Combinations from a Set

Here’s a more mathematical example. We want to know all the possible combinations of, let’s say, three things from a list of five possibilities. For example, we want to know all the teams of three people that can be chosen from a group of five people. “Dozy, Beaky, and Tich” counts as the same team as “Beaky, Tich, and Dozy”; the order within a team doesn’t matter.

And if you give this program the following input:

(combinations 3 '(a b c d e))

you get:

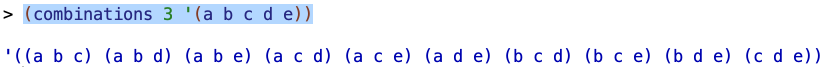
So the program is finding all the possible three-letter combinations of the letters a,b,c,d, and e.

The book says:

(If you’re trying to figure out the algorithm despite our warning, here’s a hint: All the combinations of three letters shown above can be divided into two groups. The first group consists of the ones that start with the letter A and contain two more letters; the second group has three letters not including A. The procedure finds these two groups separately and combines them into one. If you want to try to understand all the pieces, try playing with them separately, as we encouraged you to do with the pigl and acronym procedures.)

Let’s try it 🤔

Let’s look at just the prepend-every part

That worked how I expected! The name helped…
It doesn’t work if you try to append a word to just another word. It needs a whole list of words.

So prepend takes a word and appends it to each item in a sentence.

Ok let’s look at other parts of the program.

(cond ((= size 0) '(()))

cond is a special function that lets you specify what to do in a list of alternative situations. I think this first line here basically says that if the size = 0, then you return … well it looks like it’s returning an empty list within a list based on the number of parentheses. Offhand I’m not sure why it would be a list within a list. I think it’s returning something empty. I think it’s returning something empty as part of this program’s handling of the base case though, cuz we see later that the program subtracts 1 from the size at one point:

(combinations (- size 1)

And since this program recursively calls itself, I think that subtraction is something that is going to happen repeatedly, until the number gets to 0.

The other possibility that occurs to me is that the (cond ((= size 0) '(())) line is meant for handling a special case where someone happens to enter 0 initially, but I don’t think that’s the point of it.

The next line I’m going to look at is

((empty? set) '())

So this says that if set is empty, return an empty list.

This gives you an idea of how empty? works.

One part of the program is:

(combinations size (butfirst set))))))

butfirst returns all but the first item in a list:

But if the list only has one value and you call butfirst on it…

…you get an empty list. I think the point of ((empty? set) '()) is to catch when this happens.

So now let’s look at the part highlighted in blue:

(first set) gets the first item in the set (e.g. the letter “a”). prepend-every prepends that item to the result of calling

So let’s think back to (combinations 3 '(a b c d e)). the letter a would be getting prepended to combinations (3 - 1) '(b c d e). So a would be getting prepended to a bunch of 2 letter iterations of b, c, d, and e.

And then in this part of the program:

combinations calls itself with all but the first letter. And so when the resulting list '(b c d e) passes through this call to combinations, then ultimatelyb will wind up getting appended to some 2 letter iterations of c, d, and e, similar to what I describe with a above.

Okay. I think I get the general idea of how it works. Good enough for now anyways.

Example: Factorial

This one is pretty straightforward.

If n = 0 it returns 1, otherwise it multiples the value of n by the result of running factorial (- n 1)) until you get to 1.

Exercises

1.1 Do 20 push-ups.

💪

1.2 Calculate 1000 factorial by hand and see if the computer got the right answer.

No 🙂

1.3 Create a file called acronym.scm containing our acronym program, using the text editor provided for use with your version of Scheme. Load the file into Scheme and run the program. Produce a transcript file called acronym.log, showing your interaction with Scheme as you test the program several times, and print it.

The built-in DrRacket logging function gave me weird output so I just pasted the content of the interactions window into a file.

End of Chapter Review

My Prior Learning Efforts for this Chapter

I couldn’t find any work that I’d done on this chapter previously. I think that’s notable. In light of the amount of stuff I wrote here, it’s actually pretty astonishing.

Other People’s Learning Efforts for this Chapter

AnneB wrote a bunch of posts on this chapter in February of this year. I’m not actually done going through all of them, but I think the amount of effort she put into going step by step, testing things out, and sharing errors she was running into, is really great.

Learning Methodology Review

I did an okay job of writing out my thoughts and thought process for most things.

I didn’t make use of trees. I should work on that.

I got stuck trying to describe part of the ice cream choices example. A tree would have possibly helped. One thing I had an issue with was not being sure the best way to organize such a tree. If I had read through the emails early, I would have seen this tree from AnneB from which I could have drawn some inspiration.

A related thought on getting stuck on stuff – I think getting stuck is bad. On the other hand, I think that only doing exactly what the book tells you at the time that it tells you to do it is also bad. You should have some energy and should try to see how far their reason can carry them in thinking about things, and not need the permission of the book to do so. But if you’re not practiced at making your own judgments about what to try and how long to spend on it, you might waste some time while you figure that out. I don’t have a great solution to this issue at the moment.