Practicing Program Logic
Exercise 1
I made up this silly procedure to work on thinking about the logic of a program. The idea is that if x y and z are all true, you get the over 9000 message returned. If either x and y, x and z, or y and z are true, you get the 8000 message returned. If only one of x, y, or z is true, you get the 3000 message returned. If none are true, you get the message about low energy returned.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
|
(define (logical-power-level x y z)
(cond ((and x y z)'(Logical power level over 9000!))
((or
(and x y)
(and x z)
(and y z))
'(Logical power level is only 8000))
((or x y z)'(Logical power level a very weak 3000 - Sad!))
(else '(Low logical energy!))))
(logical-power-level #f #f #f)
; '(Low logical energy!)
(logical-power-level #f #t #f)
; '(Logical power level a very weak 3000 - Sad!)
(logical-power-level #f #t #t)
;'(Logical power level is only 8000)
(logical-power-level #t #t #t)
; '(Logical power level over 9000!)
|
Exercise 2 – Requirements for Amending the Constitution
This is an exercise to practice trying different ways of logically representing a procedure.
Here are requirements for amending the U.S. Constitution stated “negatively”:
You CAN’T amend the U.S. Constitution if:
1) you have fewer than 290 votes in the House, OR
2) you have fewer than 67 votes in the Senate, OR
3) fewer than 38 states have ratified the Amendment.
If any one of these numbered statements is true, an amendment fails. Any one of these things being true, independently, makes an amendment passing impossible.
Here is an implementation of the above using if with some test cases:
|
1
2
3
4
5
6
7
8
9
10
11
12
|
(define (amend-constitution1 house senate states)
(if (or (< house 290)
(< senate 67)
(< states 38))
#f #t))
(amend-constitution1 291 66 39)
;#f
(amend-constitution1 291 68 39)
;#t
|
Initially I put the parameters and the numbers in the wrong order (e.g. i had it as < 290 house) but I caught this error quickly.
This tree has logic which corresponds to the procedure above:

Another way to think of the procedure is “positively” as follows:
You can amend the U.S. Constitution if:
1) you have 290 votes or greater in the House, AND
2) you have 67 votes or greater in the Senate, AND
3) you have 38 states or greater that ratify the Amendment.
All of these must be true, together, for an amendment to succeed. If any one of them is false, the Amendment fails.
It’s a bit easier to represent the program in code by thinking of it in this way:
|
1
2
3
|
(define (amend-constitution2 house senate states)
(and (>= house 290)(>= senate 67)(>= states 38)))
|
Here is a tree for this way of doing it:
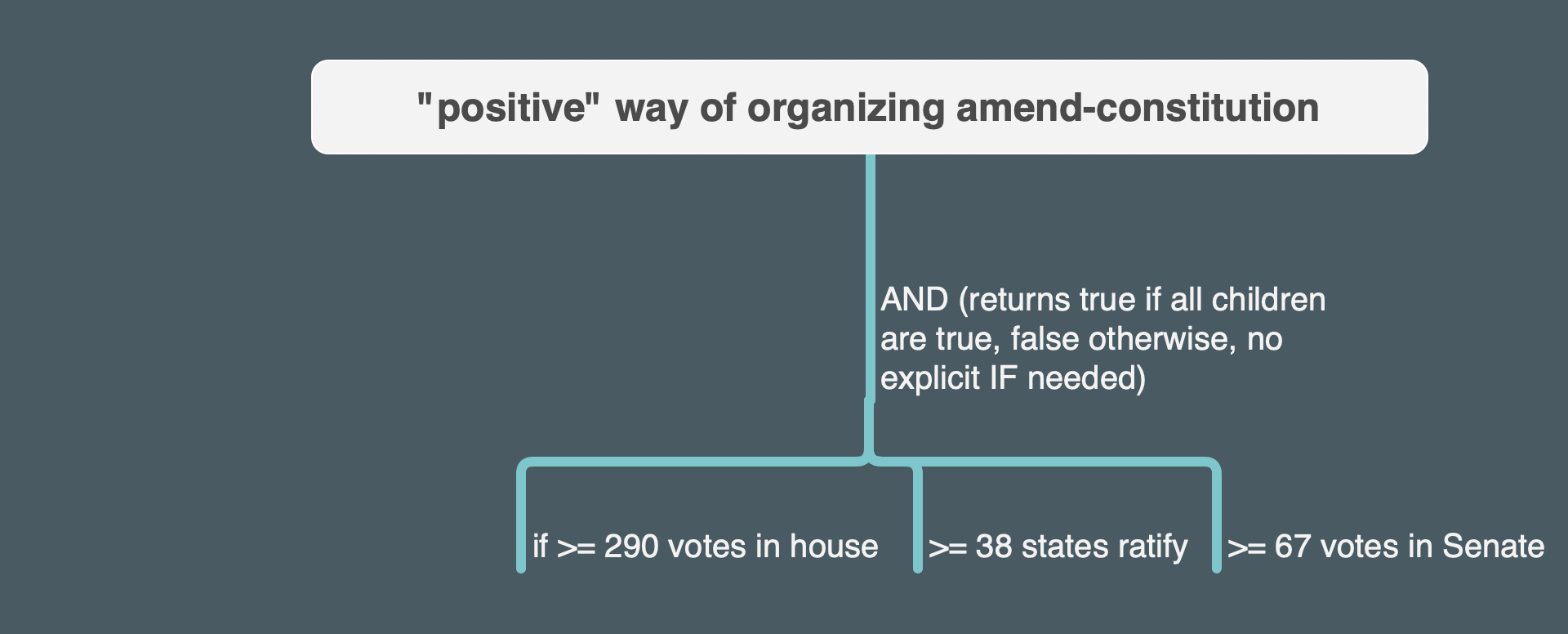
It’s easier because with this way of framing things, you can rely on the value the and returns without needing to add the complication of an if. The if was necessary in the previous version because we wanted to return false if any of the expressions that were governed by/children of the or returned true. But with this way of organizing the program, we want the expression to return true if all the expressions that are governed by/children of the and return true, and to return false otherwise. Since the output we want matches how the and works logically, we don’t need the if statement.
Thinking about different ways of organizing a program and which ways might be simpler seems like it could be quite important for effective programming.