Taking a break from the Simply Scheme book to work on some exercises of my own in order to develop some skills.
Composability of If
Exercise 1
I made up this exercise myself to work on internalizing the idea of the if procedure being composable that is discussed in chapter 6 of Simply Scheme. The program figures out whether it is election day based on user input
|
1
2
3
4
5
6
|
(define (election-day month day year)
(se 'It
(if (and (= 11 month)(= 3 day)(= 2020 year))
'(is Election Day)
'(is not Election Day))))
|
Test cases:
|
1
2
3
4
5
6
|
(election-day 11 3 2020)
It is Election Day
(election-day 11 4 2020)
It is not Election Day
|
Exercise 2
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
|
(define (bank-account-status amount)
(se '(Your account)
(if (< amount 0)
(se '(is overdrawn by) (word amount) 'dollars)
(se 'balance 'is (word "$" amount) 'dollars))))
(bank-account-status -50)
;'(Your account is overdrawn by -50 dollars)
(bank-account-status 200)
;'(Your account balance is $200 dollars)
|
Ran into an issue with this one. I initially didn’t use (se for the parts inside the if. I was thinking that I should just be able to pass multiple arguments to the se for the overall program – the one next to '(Your account). se does indeed take multiple arguments, but if does not, so if you want to use if like I do you have to group the things together. And you can’t just call procedures from inside a sentence – you can’t do e.g.
|
1
2
|
'(is overdrawn by (word '$ 500) 'dollars)
|
If I just enter that in Scheme, I get back '(is overdrawn by (word '$ 500) 'dollars). Scheme thinks the stuff inside the attempted invocation of word is just part of the sentence. So for what I want to do above, I need something that will let me call stuff like word and combine that with other stuff, grouping that into a single argument which the if can return and which the first se can take as an argument. And for my purposes se is what does that.
Nested Ifs
Exercise 1
I made a program to test my understanding of how to use nested if procedures.
Context: For U.S. Presidential elections, if no one wins a majority of electoral votes, then the incoming (newly-elected) House of Representatives selects the President, and each state House delegation from the states gets 1 vote. So the party that controls a majority of state House delegations in the incoming House of Representatives will pick the President.
There are 538 Electoral Votes up for grabs. I assume that it’s a two-man race and no votes will go to anyone else.
The program attempts to represent the following state of affairs:
– If Trump gets less than 50% of electoral votes (less than 269), that’s an outright loss. So he just loses, the end.
– If Trump gets exactly 50% of electoral votes (exactly 269), then he wins if the GOP controls a majority of the state delegations in the House. Trump loses if they do not control a majority of state House delegations.
– If Trump gets more than 50% of electoral votes (270 or higher) then he just wins.
The way I actually represented this in the program was as follows:
If Trump gets less than 269 electoral votes, he loses. Alternatively, we go to if #2.
Within if #2, if Trump has exactly 269 electoral votes, then we go to the next if statement. Otherwise, Trump wins (sine we covered \< 269 and = 269, > 269 is the only possibility left, and Trump wins in that case).
Within if #3 (where, again, Trump has exactly 269 electoral votes), if house-state-delegation-control does NOT equal gop, Trump loses. Otherwise, he wins.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
|
<br /><br />(define (election-result trump-evs house-state-delegation-control)
(if (< trump-evs 269)
'(Trump loses)
(if (= trump-evs 269)
(if (not (equal? house-state-delegation-control 'gop))
'(Trump loses)
'(Trump wins!))
'(Trump wins!))))
; test cases:
(election-result 268 'gop)
;'(Trump loses)
(election-result 269 'gop)
;'(Trump wins!)
(election-result 269 'dem)
;'(Trump loses)
(election-result 270 'dem)
;'(Trump wins!)
(election-result 270 'gop)
;'(Trump wins!)
|
I made a tree of the logic of this program. I found the tree extremely helpful.

Analysis of buntine’s Valid Date Range Checker
I liked how a github user called buntine solved one of the Scheme problems (regarding a valid date range checker). His solution is here and pasted below. I wanted to understand the program better, so i decided to try describing it in words.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
|
(define (divisible? x y)
(= (remainder x y) 0))
(define (valid-range? n bound)
(and (number? n) (> n 0) (> (+ 1 bound) n)))
(define (days-in-month m d y)
(cond
((= m 1) 31)
((= m 2)
(if (divisible? y 4)
(if (divisible? y 100)
(if (divisible? y 400)
29 28)
29)
28))
((= m 3) 31)
((= m 4) 30)
((= m 5) 31)
((= m 6) 30)
((= m 7) 31)
((= m 8) 31)
((= m 9) 31)
((= m 10) 30)
((= m 11) 30)
((= m 12) 31)
(else 0)))
(define (valid-date? m d y)
(and (valid-range? m 12)
(valid-range? d (days-in-month m d y))
(number? y)))
|
February Logic
I made a tree of the logic of the part of the program that handles February in order to help me understand it. I found it extremely helpful for this purpose.
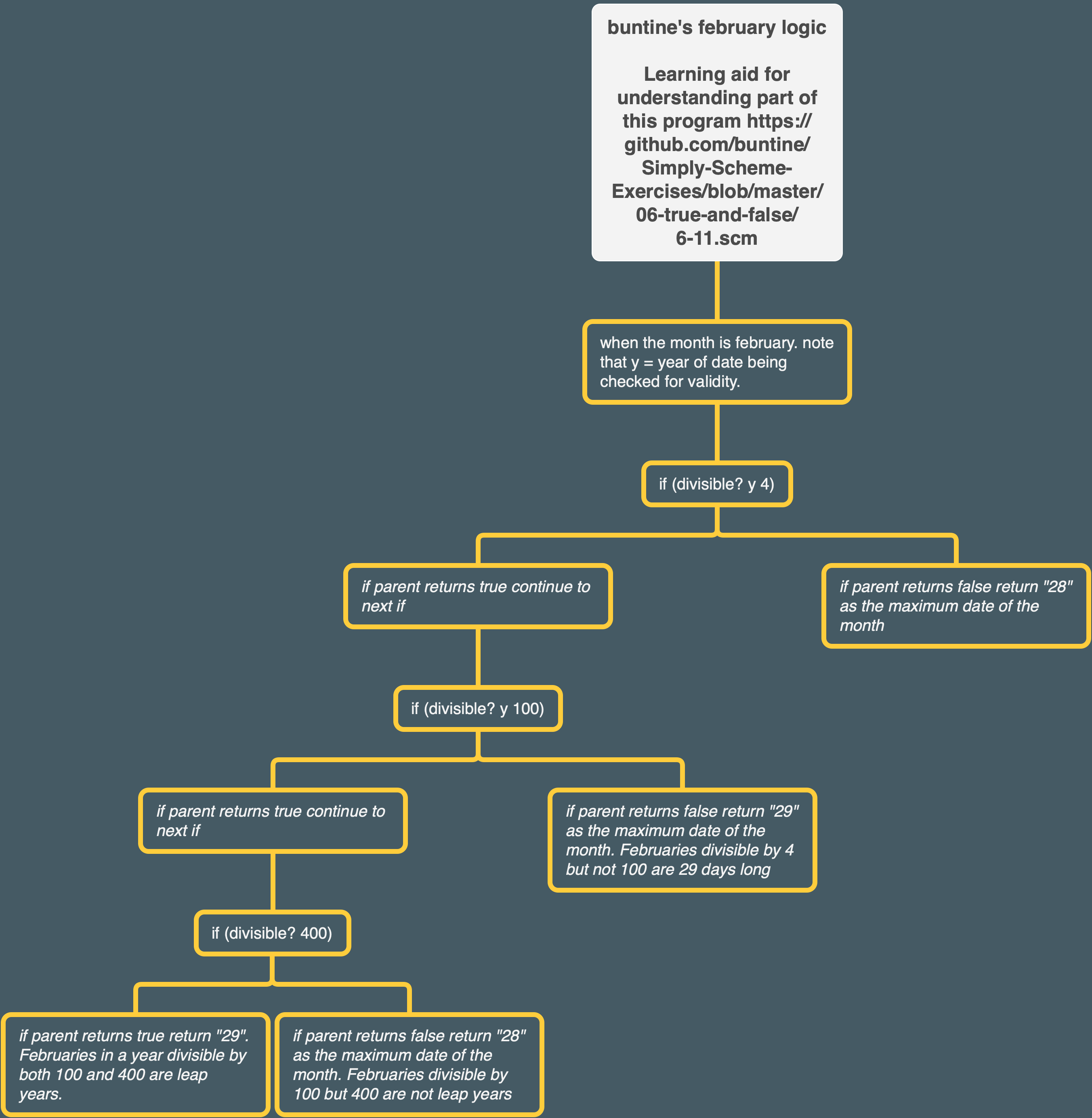
The Program Generally
Commenting on the program as I go along, skipping divisible:
|
1
2
3
|
(define (valid-range? n bound)
(and (number? n) (> n 0) (> (+ 1 bound) n)))
|
This predicate helper function offers a general solution to the problem of wanting to find whether a number is in a valid range. It checks if an argument is i) a number, and ii) greater than 0, and iii) less than a bound which is defined by the second argument passed into the program. If all these conditions are met, it returns #t. Otherwise, it returns #f.
days-in-month is a helper procedure that returns the number of days in a month depending on the month and year provided. The February logic is addressed in my tree above. If the value of the month is anything other than 1 through 12, days-in-month returns 0.
Finally, the main program:
|
1
2
3
4
5
|
(define (valid-date? m d y)
(and (valid-range? m 12)
(valid-range? d (days-in-month m d y))
(number? y)))
|
this program makes two calls to the valid-range? procedure. the first checks that the number of months is 1 through 12 (the 12 gets used as the bound). the second call to valid-range? is more interesting. the days-in-month procedure is used to generate the bound for checking the validity of the value for days d. Finally, the year is checked to ensure it is a number. If all these checks are passed, the entire procedure returns #t.