https://people.eecs.berkeley.edu/~bh/ssch16/match.html
For this chapter I judged it wise to proceed in the form of comments on selective quotes from the subsections of the chapter. I didn’t have any comments on the “Naming the Matched Text” , “Abstract Data Types”, “Backtracking and Known-Values“, or “How We Wrote It” subsections so those aren’t represented below. I did the first set of exercises at the point the book suggested. I was unable to solve one of the exercises in the second set. I was unable to find someone else who had done these exercises and posted them online and so I couldn’t check my answers. I skipped 16.22.
Problem Description
It’s time for another extended example in which we use the Scheme tools we’ve been learning to accomplish something practical. We’ll start by describing how the program will work before we talk about how to implement it.
You can load our program into Scheme by typing
|
1
2
|
(load "match.scm")
|
I managed to get this to work by using the whole path to match.scm in quotes.
A pattern matcher is a commonly used procedure whose job is to compare a sentence to a range of possibilities. An example may make this clear:
|
1
2
3
4
5
6
7
8
9
|
> (match '(* me *) '(love me do))
#T
> (match '(* me *) '(please please me))
#T
> (match '(* me *) '(in my life))
#F
|
Note that the program doesn’t actually return true and false. In a case where no pattern is found, it returns 'failed‘, which evaluates as true. I was confused by this initially.
The first argument,
(* me *), is a pattern. In the pattern, each asterisk (*) means “any number of words, including no words at all.” So the entire pattern matches any sentence that contains the word “me” anywhere within it. You can think ofmatchas a more general form ofequal?in the sense that it compares two sentences and tells us whether they’re the same, but with a broader meaning of “the same.”Our pattern matcher will accept patterns more complicated than this first example. There are four special characters that indicate unspecified parts of a pattern, depending on the number of words that should be allowed:
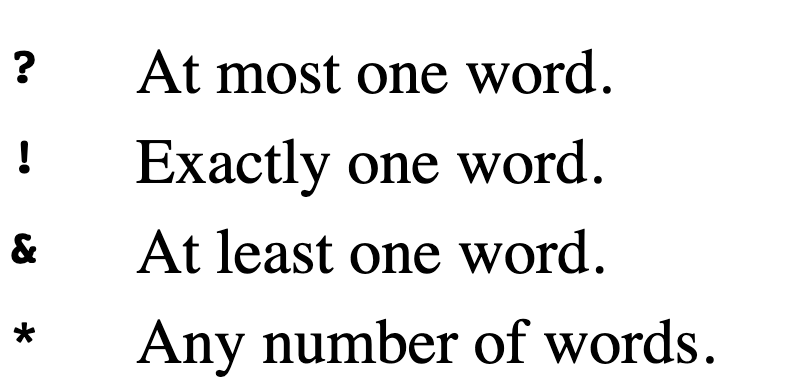
These characters are meant to be somewhat mnemonic. The question mark means “maybe there’s a word.” The exclamation point means “precisely one word!” (And it’s vertical, just like the digit 1, sort of.) The ampersand, which ordinarily means “and,” indicates that we’re matching a word and maybe more. The asterisk doesn’t have any mnemonic value, but it’s what everyone uses for a general matching indicator anyway.
We can give a name to the collection of words that match an unspecified part of a pattern by including in the pattern a word that starts with one of the four special characters and continues with the name. If the match succeeds,matchwill return a sentence containing these names and the corresponding values from the sentence:

I didn’t find the explanation about super clear but I think what’s happening here is:
The * in the first argument, at the beginning of *start*, tells match to look for any number of words in the second argument to appear before me. Since love appears before me, a pattern match is found. By putting the * at the beginning of the word start, we can see both the word we’ve embedded the * in and the words that are being matched in our return value for match, whereas otherwise the return value on a match would be empty. If we had additional words at the beginning of the second argument (before the “me”), those would be matched as well and show up in our result

And the same would be true with more words after the “me”:

In these examples [referring to the examples captioned “Four Examples”], you see that
matchdoesn’t really return#tor#f; the earlier set of examples showed a simplified picture. In the first of the new examples,
meaning this one
|
1
2
3
4
|
> (match '(*start me *end) '(love me do))
(START LOVE ! END DO !)
|
the special pattern word
*startis allowed to match any number of words, as indicated by the asterisk. In this case it turned out to match the single word “love.”Matchreturns a result that tells us which words of the sentence match the named special words in the pattern. (We’ll call one of these special pattern words a placeholder.) The exclamation points in the returned value are needed to separate one match from another.
So with (match '(* me *) '(love me do)) we get a blank return because we’ve got no special pattern words.
But with '(*start me *end) '(love me do ninjstars) we see our special pattern word, followed by the word that the * in the pattern word matched on, love. Then we get an exclamation point indicating that that “start love” represents the first special-pattern-word/matched word group. We don’t see a match for the “me” which is consistent with the previous results.We then see the special-pattern-word again, followed by the word it matched, followed by another exclamation point indicating a matching group.
(In the second example, the name
endwas matched by an empty set of words.)
|
1
2
3
4
|
>(match '(*start me *end) '(please please me))
(START PLEASE PLEASE ! END !)
|
*start* matches both copies of “please” since * matches any number of words. So the exclamation point indicating a break between matches comes after the second please. The “me” is not reflected in the result. The *end* matches on an empty set of words (not super clear on this).
In the third example, the match was successful, but since there were no placeholders the returned sentence was empty.
|
1
2
3
4
|
> (match '(mean mr mustard) '(mean mr mustard))
()
|
This one makes sense.
If the match is unsuccessful,
matchreturns the wordfailed.[1]
The footnote at the end of this paragraph notes:
Why not return the sentence if successful or
#fotherwise? That would be fine in most versions of Scheme, but as we mentioned earlier, the empty sentence()is the same as the false value#fin some dialects. In those Schemes, a successfully matched pattern with no named placeholders, for which the program should return an empty sentence, would be indistinguishable from an unmatched pattern.
Ah ok, I was wondering about returning failed instead of #f. So we’re returning failed and not #f in order to maintain a distinction between unmatched patterns and matched patterns with no placeholders in some Scheme dialects.
If the same placeholder name appears more than once in the pattern, then it must be matched by the same word(s) in the sentence each time:
|
1
2
3
4
|
> (match '(!twice !other !twice) '(cry baby cry))
(TWICE CRY ! OTHER BABY !)
|
|
1
2
3
4
|
> (match '(!twice !other !twice) '(please please me))
FAILED
|
In the first example, the same placeholder name, !twice, is paired off with the same word in the second argument, so it’s a match.
In the second example, !twice tries to match on please and me respectively, so it’s a fail.
Some patterns might be matchable in more than one way. For example, the invocation
|
1
2
|
(match '(*front *back) '(your mother should know))
|
might return any of five different correct answers:

for me it returned:
![]()
We arbitrarily decide that in such cases the first placeholder should match as many words as possible, so in this case match will actually return the first of these answers.
Before continuing, you might want to look at the first batch of exercises at the end of this chapter, which are about using the pattern matcher. (The rest of the exercises are about the implementation, which we’ll discuss next.)
Exercises About Using the Pattern Matcher
16.1
Design and test a pattern that matches any sentence containing the word
Cthree times (not necessarily next to each other).
Answer: (* c * c * c)
* matches any number of words. This includes no words at all.

![]()
and this one fails cuz it only has two c’s
16.2
Design and test a pattern that matches a sentence consisting of two copies of a smaller sentence, such as
(a b a b).
Answer: (!this !that !this !that)
![]()

16.3
Design and test a pattern that matches any sentence of no more than three words.
Answer: (! ! !)
(match '(! ! !)'(c c c))

16.4
Design and test a pattern that matches any sentence of at least three words.
Answer: (& & &)
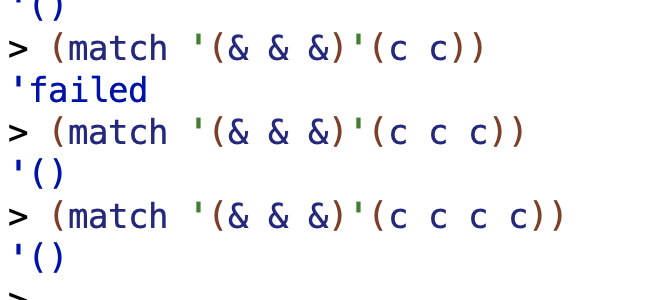
16.5
Show sentences of length 2, 3, and 4 that match the pattern
(*x *y *y *x)
For each length, if no sentence can match the pattern, explain why not.
4 words:
|
1
2
|
(match '(*x *y *y *x)'(potato tomato tomato potato))
|
![]()
From earlier, remember that “If the same placeholder name appears more than once in the pattern, then it must be matched by the same word(s) in the sentence each time”.
2 words:
|
1
2
|
(match '(*x *y *y *x)'(a a))
|

3 words won’t work. 2 words works because the two*x terms can match on the a’s, and then the two *y terms can match on nothing. But with 3 words we can’t have a value matching on nothing or an empty set or whatever. with 3 words, three of the terms in the pattern are going to correspond to words in the second argument. But this pattern requires 2 matching pairs. So 3 words won’t work.
16.6
Show sentences of length 2, 3, and 4 that match the pattern
(*x *y &y &x)For each length, if no sentence can match the pattern, explain why not.
So the (&y &x) values need to have at least one word.
Four words works:
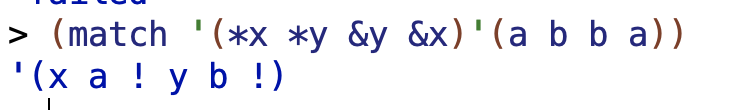
If we need to have at least one word for &y &x, we can’t match them on the empty word, so that can’t let us get away with having one of the pairs of values match on empty, which is the trick we used last time to have a sentence with a length of two words. So 2 words won’t work.
Likewise, if we need at least one word for &y &x, we’ve got to have words in those sentence which are identical for there to be a match on *x *y. So 4 words is actually the minimum size sentence that will match.
16.7
List all the sentences of length 6 or less, starting with
a b a, that match the pattern(*x *y *y *x)
The empty sentence matches (I know I’m not starting from (a b a); I just wanna list them all):
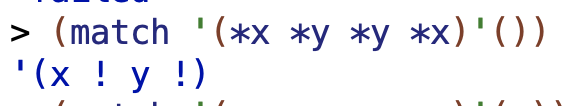
1 word won’t match.
2 words matches on a a, as described before in 16.5.
The 3 word case a b a doesn’t match, so I’m not sure why they’re bringing it up:
![]()
4 words:
the pattern matches on a b b a, as described before.
the pattern matches on '(a a a a))
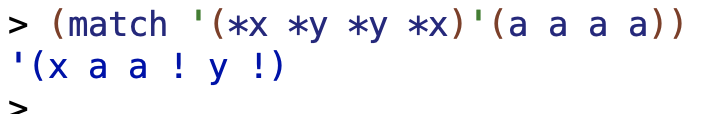
Why? The match for*x can be multiple words long, and so it matches on a a. the *y can be 0 words long, and so matches on nothing.
The pattern won’t match on five words.
6 words:
The pattern will match on '(a a a a a a)). each *x matches on a a a and the *y matches on nothing:
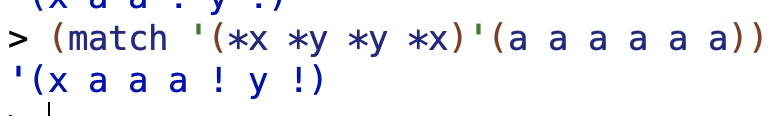
The pattern will match on '(a a b b a a). Each *x matches on a a and each *y matches on b.

The pattern will match on '(a b b b b a). Each *x matches on a and each *y matches on b b.
![]()
Implementation
When Are Two Sentences Equal?
Our approach to implementation will be to start with something we already know how to write: a predicate that tests whether two sentences are exactly equal. We will add capabilities one at a time until we reach our goal.
Suppose that Scheme’s primitive
equal?function worked only for words and not for sentences. We could write an equality tester for sentences, like this:
|
1
2
3
4
5
6
7
|
(define (sent-equal? sent1 sent2)
(cond ((empty? sent1)(empty? sent2))
((empty? sent2) #f)
((equal? (first sent1) (first sent2))
(sent-equal? (bf sent1) (bf sent2)))
(else #f)))
|
Two sentences are equal if each word in the first sentence is equal to the corresponding word in the second. They’re unequal if one sentence runs out of words before the other.
The first cond expression efficiently tests whether both sentences are empty by using the second test as the expression that gets evaluated if the first is true. Clever.
The second cond expression, which only will get evaluated if the first one is false, tests whether the second sentence is empty and returns false if so.
The third cond expression tests if the first word of the two sentences are equal, and makes a recursive call if so.
The else address the case when the first words of the sentences are not equal, returning false in that case.
Why are we choosing to accept Scheme’s primitive word comparison but rewrite the sentence comparison? In our pattern matcher, a placeholder in the pattern corresponds to a group of words in the sentence. There is no kind of placeholder that matches only part of a word. (It would be possible to implement such placeholders, but we’ve chosen not to.) Therefore, we will never need to ask whether a word is “almost equal” to another word.
When Are Two Sentences Nearly Equal?
Pattern matching is just a more general form of this
sent-equal?procedure. Let’s write a very simple pattern matcher that knows only about the “!” special character and doesn’t let us name the words that match the exclamation points in the pattern. We’ll call this onematch?with a question mark because it returns just true or false.
|
1
2
3
4
5
6
7
8
9
10
|
(define (match? pattern sent) ;; first version: ! only
(cond
((empty? pattern)(empty? sent))
((empty? sent) #f)
((equal? (first pattern) '!)
(match? (bf pattern) (bf sent)))
((equal? (first pattern) (first sent))
(match? (bf pattern) (bf sent)))
(else #f)))
|

This program is exactly the same as
sent-equal?, except for the highlightedcondclause. We are still comparing each word of the pattern with the corresponding word of the sentence, but now an exclamation mark in the pattern matches any word in the sentence. (Iffirstofpatternis an exclamation mark, we don’t even look atfirstofsent.)

Our strategy in the next several sections will be to expand the pattern matcher by implementing the remaining special characters, then finally adding the ability to name the placeholders. For now, when we say something like “the
*placeholder,” we mean the placeholder consisting of the asterisk alone. Later, after we add named placeholders, the same procedures will implement any placeholder that begins with an asterisk.
Matching with Alternatives
The
!matching is not much harder thansent-equal?, because it’s still the case that one word of the pattern must match one word of the sentence. When we introduce the?option, the structure of the program must be more complicated, because a question mark in the pattern might or might not be paired up with a word in the sentence. In other words, the pattern and the sentence might match without being the same length.
The new portion uses an if expression nested in the cond clause if ? is the first word in the pattern sentence. In that case, the if first checks if the sent is empty. If so, it makes a recursive call to match? with bf pattern and an empty sentence. This handles a case where the sentence is empty but there are more terms in the pattern to check (such as more ? values that might successfully match on an empty sentence).
If sent is not empty, the if expression tests whether one of two of the following things is true:
1. a recursive call to match? with bf pattern and bf sent returns true.
2. a recursive call to match? with bf pattern and sent returns true.
If either one of these returns true, match? will return true. Since these are recursive calls, there might be quite a number of computational steps before they actually get evaluated.
Why are we testing both bf sent and sent? More specifically, while (match? (bf pattern) (bf sent)) makes some intuitive sense based on the book so far, why do we care about (match? (bf pattern) sent))? Why do we need to test sent further (as opposed to bf sent) given that sent is what we’re testing right now? We know that ? can match on no word. So we need to see whether, if we take the ? out of the equation, the remainder of the pattern and sentence match. That’s what the (match? (bf pattern) sent)))) is for.

If we edit the procedure’s code to remove the (match? (bf pattern) sent)))), then match '(? a b) '(a b)) returns false. So this code is capturing an essential case.
Note that the new
condclause comes before the check to see ifsentis empty. That’s becausesentmight be empty and a pattern of(?)would still match it.
In that case, we want to return #t, not #f like in our empty sentence check.
But if the sentence is empty, we know that the question mark doesn’t match a word, so we just have to make sure that the
butfirstof the pattern contains nothing but question marks. (We don’t have a predicate namedall-question-marks?; instead, we usematch?recursively to make this test.)
So if the sentence is empty, we just butfirst through the pattern, not the sentence. Ultimately, if we run out of pattern cuz all the patterns are question marks, then we will hit (cond ((empty? pattern) (empty? sent)) and return true.
In general, a question mark in the pattern has to match either one word or zero words in the sentence. How do we decide? Our rule is that each placeholder should match as many words as possible, so we prefer to match one word if we can. But allowing the question mark to match a word might prevent the rest of the pattern from matching the rest of the sentence.
Compare these two examples:
|
1
2
3
4
5
6
7
8
|
> (match? '(? please me) '(please please me))
#T
> (match? '(? please me) '(please me))
#T
|
In the first case, the first thing in the pattern is a question mark and the first thing in the sentence is “please,” and they match. That leaves “please me” in the pattern to match “please me” in the sentence.
So the first case is handled by the (match? (bf pattern) (bf sent) part of the or I was just discussing.
In the second case, we again have a question mark as the first thing in the pattern and “please” as the first thing in the sentence. But this time, we had better not use up the “please” in the sentence, because that will only leave “me” to match “please me.” In this case the question mark has to match no words.
The second example is handled by the (match? (bf pattern) sent)). We treat the question mark as matching no words, and do not “use up” the “please”.
To you, these examples probably look obvious. That’s because you’re a human being, and you can take in the entire pattern and the entire sentence all at once. Scheme isn’t as smart as you are; it has to compare words one pair at a time. To Scheme, the processing of both examples begins with question mark as the first word of the pattern and “please” as the first word of the sentence. The pattern matcher has to consider both cases.
How does the procedure consider both cases? Look at the invocation oforby thematch?procedure. There are two alternatives; if either turns out true, the match succeeds. One is that we try to match the question mark with the first word of the sentence just as we matched!in our earlier example-by making a recursive call on thebutfirsts of the pattern and sentence. If that returns true, then the question mark matches the first word.
The second alternative that can make the match succeed is a recursive call tomatch?on thebutfirstof the pattern and the entire sentence; this corresponds to matching the?against nothing.[2]
Let’s tracematch?so that you can see how these two cases are handled differently by the program.

A bit tricky but I think I’ve got the idea 🙂
Backtracking
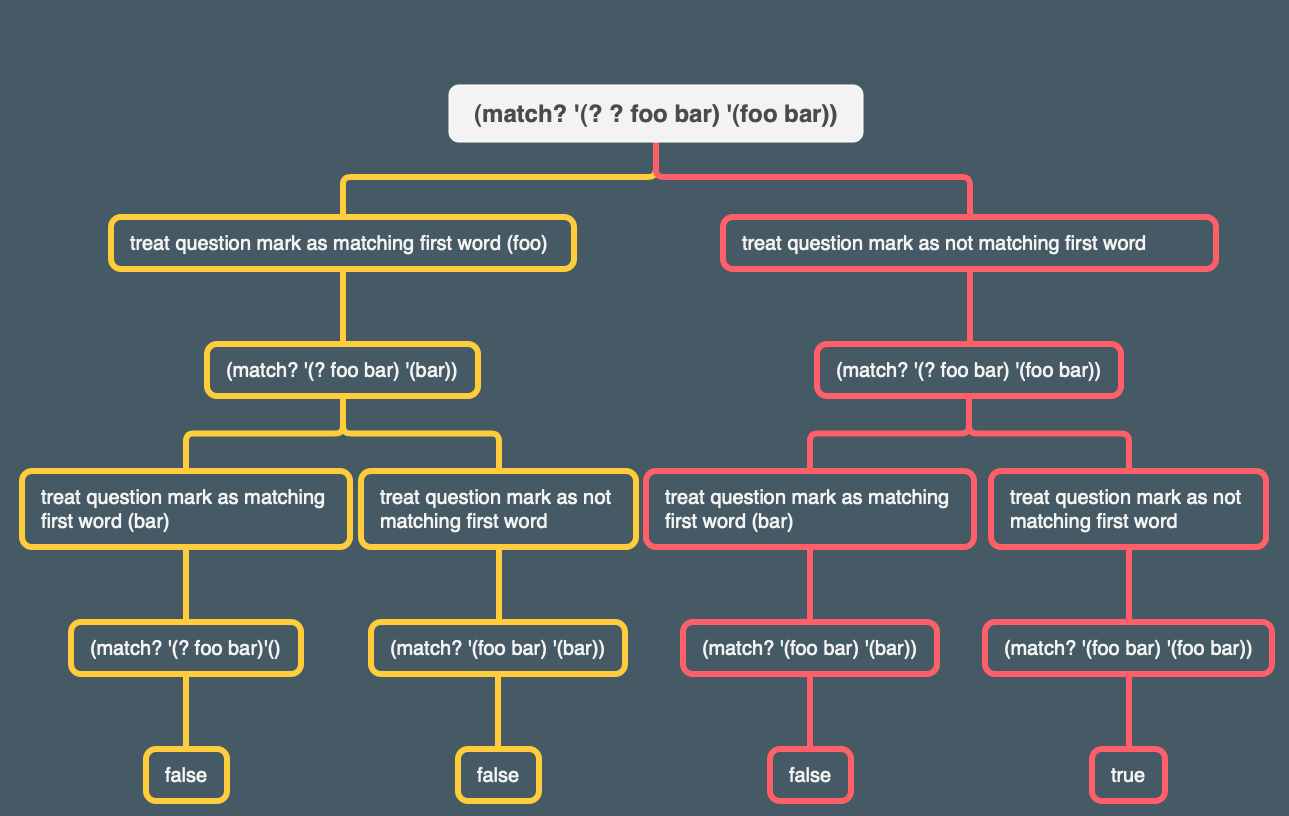
Here are some traced examples involving patterns with two question marks, to show how the result of backtracking depends on the individual problem.

In this first example, the first question mark tries to match the word
bar, but it can’t tell whether or not that match will succeed until the recursive call returns. In the recursive call, the second question mark tries to match the wordfoo, and fails. Then the second question mark tries again, this time matching nothing, and succeeds. Therefore, the first question mark can report success; it never has to try a recursive call in which it doesn’t match a word.
I made a tree to help show what’s going on (I labeled the results in boolean terms even though in retrospect that’s not quite accurate):
In our second example, each question mark will have to try both alternatives, matching and then not matching a word, before the overall match succeeds.

Another tree:
The first question mark tries to match the word
fooin the sentence, leaving the pattern(? foo bar)to match(bar). The second question mark will try both matching and not matching a word, but neither succeeds. Therefore, the first question mark tries again, this time not matching a word. The second question mark first tries matchingfoo, and when that fails, tries not matching anything. This last attempt is successful.
Yep, makes sense.
Matching Several Words
The next placeholder we’ll implement is
*. The order in which we’re implementing these placeholders was chosen so that each new version increases the variability in the number of words a placeholder can match. The!placeholder was very easy because it always matches exactly one word; it’s hardly different at all from a non-placeholder in the pattern. Implementing?was more complicated because there were two alternatives to consider. But for*, we might match any number of words, up to the entire rest of the sentence.Our strategy will be a generalization of the
?strategy: Start with a “greedy” match, and then, if a recursive call tells us that the remaining part of the sentence can’t match the rest of the pattern, try a less greedy match.The difference between
?and*is that?allows only two possible match lengths, zero and one. Therefore, these two cases can be checked with two explicit subexpressions of anorexpression. In the more general case of*, any length is possible, so we can’t check every possibility separately. Instead, as in any problem of unknown size, we use recursion. First we try the longest possible match; if that fails because the rest of the pattern can’t be matched, a recursive call tries the next-longest match. If we get all the way down to an empty match for the*and still can’t match the rest of the pattern, then we return#f.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
|
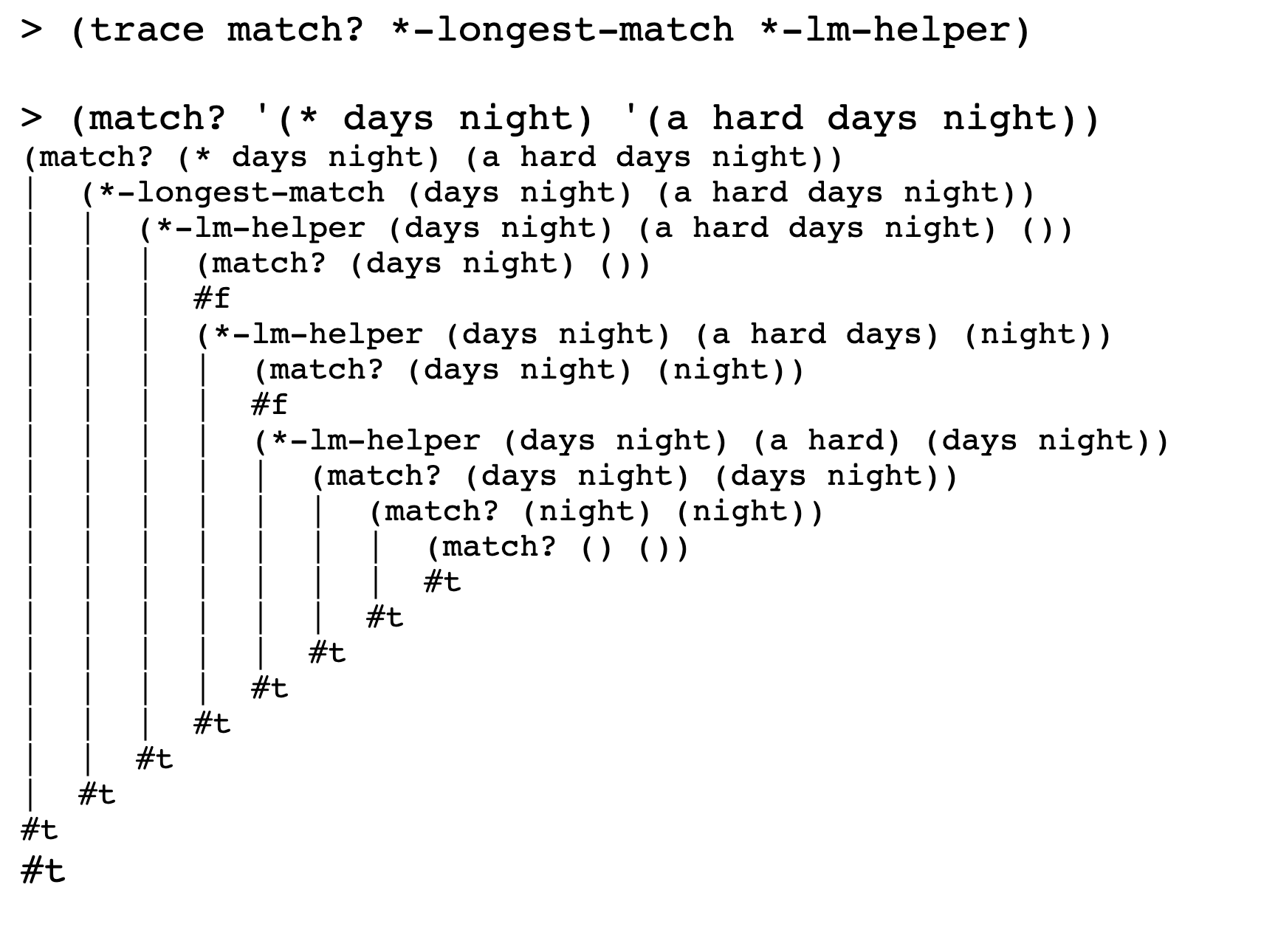
(define (match? pattern sent) ;; third version: !, ?, and *
(cond ((empty? pattern)
(empty? sent))
((equal? (first pattern) '?)
(if (empty? sent)
(match? (bf pattern) '())
(or (match? (bf pattern) (bf sent))
(match? (bf pattern) sent))))
((equal? (first pattern) '*)
(*-longest-match (bf pattern) sent))
((empty? sent) #f)
((equal? (first pattern) '!)
(match? (bf pattern) (bf sent)))
((equal? (first pattern) (first sent))
(match? (bf pattern) (bf sent)))
(else #f)))
(define (*-longest-match pattern-rest sent)
(*-lm-helper pattern-rest sent '()))
(define (*-lm-helper pattern-rest sent-matched sent-unmatched)
(cond ((match? pattern-rest sent-unmatched) #t)
((empty? sent-matched) #f)
(else (*-lm-helper pattern-rest
(bl sent-matched)
(se (last sent-matched) sent-unmatched)))))
|
So in the match? procedure we have a new cond clause that checks whether or not the first word of pattern is equal to *. If so, we invoke *-longest-match with bf pattern and sent.
*=longest-match invokes a helper procedure with the remainder of the pattern (excluding the * we already butfirst-ed past), sent and an empty sentence. The empty sentence
*-1m-helper is where the action happens:
The real work is done by
*-lm-helper, which has three arguments. The first argument is the still-to-be-matched part of the pattern, following the*placeholder that we’re trying to match now.Sent-matchedis the part of the sentence that we’re considering as a candidate to match the*placeholder.Sent-unmatchedis the remainder of the sentence, following the words insent-matched; it must matchpattern-rest.
Since we’re trying to find the longest possible match,*-longest-matchchooses the entire sentence as the first attempt forsent-matched.
This represents the “greedy” match.
Since
sent-matchedis using up the entire sentence, the initial value ofsent-unmatchedis empty.
That’s why the first value we provide for sent-unmatched is the empty sentence.
The only job of
*-longest-matchis to invoke*-lm-helperwith these initial arguments. On each recursive invocation,*-lm-helpershortenssent-matchedby one word and accordingly lengthenssent-unmatched.
Here’s an example in which the*placeholder tries to match four words, then three words, and finally succeeds with two words:
No tree here cuz I think I’ve got the idea.
Combining the Placeholders
We have one remaining placeholder,
&, which is much like*except that it fails unless it can match at least one word. We could, therefore, write a&-longest-matchthat would be identical to*-longest-matchexcept for the base case of its helper procedure. Ifsent-matchedis empty, the result is#feven if it would be possible to match the rest of the pattern against the rest of the sentence. (All we have to do is exchange the first two clauses of thecond.)
Whereas with *, you can match on zero words, with &, you need at least one word. If the sent we give to the helper procedure is empty, then no match is going to be possible. sent being empty decides the issue of whether or not there is a match definitively for &, so we want to check that first, whereas for *, a match was still possible on an empty sentence (if, for example, all the remaining values in the pattern were also *.)
|
1
2
3
4
5
|
(define (&-longest-match pattern-rest sent) (&-lm-helper pattern-rest sent '()))
(define (&-lm-helper pattern-rest sent-matched sent-unmatched) (cond ((empty? sent-matched) #f) ((match? pattern-rest sent-unmatched) #t) (else (&-lm-helper pattern-rest (bl sent-matched) (se (last sent-matched) sent-unmatched)))))
|
When two procedures are so similar, that’s a clue that perhaps they could be combined into one. We could look at the bodies of these two procedures to find a way to combine them textually. But instead, let’s step back and think about the meanings of the placeholders.
The reason that the procedures
*-longest-matchand&-longest-matchare so similar is that the two placeholders have almost identical meanings.*means “match as many words as possible”;&means “match as many words as possible, but at least one.” Once we’re thinking in these terms, it’s plausible to think of?as meaning “match as many words as possible, but at most one.” In fact, although this is a stretch, we can also describe!similarly: “Match as many words as possible, but at least one, and at most one.”
We’ll take advantage of this newly understood similarity to simplify the program by using a single algorithm for all placeholders.
How do we generalize*-longest-matchand&-longest-matchto handle all four cases? There are two kinds of generalization involved. We’ll write a procedurelongest-matchthat will have the same arguments as*-longest-match, plus two others, one for for the minimum size of the matched text and one for the maximum.
We’ll specify the minimum size with a formal parametermin. (The corresponding argument will always be 0 or 1.)Longest-matchwill pass the value ofmindown tolm-helper, which will use it to reject potential matches that are too short.
Unfortunately, we can’t use a number to specify the maximum size, because for*and&there is no maximum. Instead,longest-matchhas a formal parametermax-one?whose value is#tonly for?and!.
Our earlier, special-case versions oflongest-matchwere written for*and&, the placeholders for whichmax-one?will be false. For those placeholders, the newlongest-matchwill be just like the earlier versions. Our next task is to generalizelongest-matchso that it can handle the#tcases.
Think about the meaning of thesent-matchedandsent-unmatchedparameters in thelm-helperprocedures.Sent-matchedmeans “the longest part of the sentence that this placeholder is still allowed to match,” whilesent-unmatchedcontains whatever portion of the sentence has already been disqualified from being matched by the placeholder.
To try to be more precise, I think sent-matched is the longest part of the sentence that the placeholder might yet potentially match, depending on the outcome of further computations. Or to put it a different way, sent-matched represents the portion of the sentence that we haven’t yet refuted as a match for the placeholder.
Consider the behavior of
*-longest-matchwhen an asterisk is at the beginning of a pattern that we’re trying to match against a seven-word sentence. Initially,sent-matchedis the entire seven-word sentence, andsent-unmatchedis empty. Then, supposing that doesn’t work,sent-matchedis a six-word sentence, whilesent-unmatchedcontains the remaining word. This continues as long as no match succeeds until, near the end oflongest-match‘s job,sent-matchedis a one-word sentence andsent-unmatchedcontains six words. At this point, the longest possible match for the asterisk is a single word.
This situation is where we want to start in the case of the?and!placeholders. So when we’re trying to match one of these placeholders, our initialization procedure won’t use the entire sentence as the initial value ofsent-matched; rather, the initial value ofsent-matchedwill be a one-word sentence, andsent-unmatchedwill contain the rest of the sentence.
That makes sense.
I’ve analyzed how longest-match handles the empty sentence (in its first cond clause) in my response to question 16.8 below, so I won’t talk about that here.
For the second cond clause, longest-match checks if max-one? if true. If so, as the book says, “the initial value of sent-matched [when passed into lm-helper] will be a one-word sentence, and sent-unmatched will contain the rest of the sentence.” max-one? will be true for ? and !. Since these symbols can match on at most one word, having the initial value of sent-matched be a one-word sentence makes sense, since the other words will be irrelevant to the result in terms of matching.
For the else clause, which will cover non-empty sentences for the * and & values, the invocation is as it was in the earlier special case helper procedures.
For the lm-helper procedure, the first cond checks to see if the length of sent-matched is less than min. if so, it returns false. ! and & have a min of 1 and * and ? have a min of 0. If the length of the part of the sentence that could potentially match the symbol/placeholder falls below the min for that symbol, then no match can occur, and so lm-helper should return false.
Earlier versions of longest-match and lm-helper were for * and &, which have no maximum size.
For & we put the empty sent check before trying to match the rest of pattern to the rest of sentence.
![]()
For *, we tried to match the rest of pattern/rest of sentence first.
![]()
For our new combined procedure, we try to match before checking for the empty sentence, consistent with the previous pattern for *; however, before either of those, we check to see that the length of sent-matched is not less than min.

If sent-matched is 0 when we are matching for &, then that is less than &‘s min of 1, and so lm-helper will return false. In this case, where min is 1 and the length of sent-matched is decreasing by one as the match? procedure goes along, testing for an integer less than 1 is effectively testing for an empty sent-matched. This conforms to the pattern of cond clauses for the special case procedure for &.
On the other hand, if min is 0, as it is with *, then the first cond won’t return true for an empty sentence, because the length of sent-matched would actually need to equal -1 in order to be less than the min of 0. So in that case, the cond clause that tests for a match on the rest of pattern/rest of sentence comes before the test for the empty sentence, as was true in the special case * lm-helper procedure before. So by the use of different values for min, we can have a general procedure that achieves the same results as our multiple special case procedures.
Now we can rewrite
match?to uselongest-match.Match?will delegate the handling of all placeholders to a subprocedurematch-specialthat will invokelongest-matchwith the correct values forminandmax-one?according to the table.
|
1
2
3
4
5
6
|
(define (match? pattern sent) ;; fourth version (cond ((empty? pattern) (empty? sent)) ((special? (first pattern)) (match-special (first pattern) (bf pattern) sent)) ((empty? sent) #f) ((equal? (first pattern) (first sent)) (match? (bf pattern) (bf sent))) (else #f)))
(define (special? wd) ;; first version (member? wd '(* & ? !)))
(define (match-special placeholder pattern-rest sent) ;; first version (cond ((equal? placeholder '?) (longest-match pattern-rest sent 0 #t)) ((equal? placeholder '!) (longest-match pattern-rest sent 1 #t)) ((equal? placeholder '*) (longest-match pattern-rest sent 0 #f)) ((equal? placeholder '&) (longest-match pattern-rest sent 1 #f))))
|
The Final Version
We’re now ready to show you the final version of the program. The program structure is much like what you’ve seen before; the main difference is the database of placeholder names and values. The program must add entries to this database and must look for database entries that were added earlier. Here are the three most important procedures and how they are changed from the earlier version to implement this capability:
match-using-known-values, essentially the same as what was formerly namedmatch?except for bookkeeping details.
match-special, similar to the old version, except that it must recognize the case of a placeholder whose name has already been seen. In this case, the placeholder can match only the same words that it matched before.
longest-matchandlm-helper, also similar to the old versions, except that they have the additional job of adding to the database the name and value of any placeholder that they match.Here are the modified procedures. Compare them to the previous versions.
Let’s compare match? to its replacement, match-using-known-values:
|
1
2
3
4
5
6
7
8
9
10
|
(define (match? pattern sent) ;; fourth version
(cond ((empty? pattern)
(empty? sent))
((special? (first pattern))
(match-special (first pattern) (bf pattern) sent))
((empty? sent) #f)
((equal? (first pattern) (first sent))
(match? (bf pattern) (bf sent)))
(else #f)))
|
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
|
(define (match pattern sent)
(match-using-known-values pattern sent '()))
(define (match-using-known-values pattern sent known-values)
(cond ((empty? pattern)
(if (empty? sent) known-values 'failed))
((special? (first pattern))
(let ((placeholder (first pattern)))
(match-special (first placeholder)
(bf placeholder)
(bf pattern)
sent
known-values)))
((empty? sent) 'failed)
((equal? (first pattern) (first sent))
(match-using-known-values (bf pattern) (bf sent) known-values))
(else 'failed)))
|
match-using-known-values has some changes to its first cond consequent. Instead of returning a boolean depending on the result of empty? sent like in match?, it has an if statement that returns known-values if sent is empty? and returns failed otherwise. So basically, if we run out of pattern and we run out of sent, known-values gets returned. On the other hand, if we run out of pattern but sent is not empty, we get 'failed.
Then we have a new way of handling looking for special placeholder characters. The condition is the same, but the consequent makes use of a let and also passes in known-values to match-special, which is different than what was done before.
Everything else in match-using-known-values is similar to match? but with the required adjustments for returning failed instead of #false and for passing the known-values definition as necessary.
For match-special, here’s the previous version:
|
1
2
3
4
5
6
7
8
9
10
11
|
<br />(define (match-special placeholder pattern-rest sent) ;; first version
(cond ((equal? placeholder '?)
(longest-match pattern-rest sent 0 #t))
((equal? placeholder '!)
(longest-match pattern-rest sent 1 #t))
((equal? placeholder '*)
(longest-match pattern-rest sent 0 #f))
((equal? placeholder '&)
(longest-match pattern-rest sent 1 #f))))
|
and the final version:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
|
(define (match-special howmany name pattern-rest sent known-values)
(let ((old-value (lookup name known-values)))
(cond ((not (equal? old-value 'no-value))
(if (length-ok? old-value howmany)
(already-known-match
old-value pattern-rest sent known-values)
'failed))
((equal? howmany '?)
(longest-match name pattern-rest sent 0 #t known-values))
((equal? howmany '!)
(longest-match name pattern-rest sent 1 #t known-values))
((equal? howmany '*)
(longest-match name pattern-rest sent 0 #f known-values))
((equal? howmany '&)
(longest-match name pattern-rest sent 1 #f known-values)))))
|
The final version is similar to the earlier version, save for the final version addressing the case where a placeholder has already been seen. In that case, it defines old-value using lookup invoked with the placeholder name (for example, the twice part of the expression!twice when using !twice as a pattern) and known-values. old-value represents the values matched by a previous instance of the placeholder. length-ok? uses old-value and howmany (howmany representing the special character at the start of a placeholder – the ! from !twice, for instance) to see if old-value is consistent with the howmany part of the placeholder.
For example, if the pattern is
|
1
2
|
(*stuff and !stuff)
|
and the database says that the placeholder
*stuffwas matched by three words from the sentence, then the second placeholder!stuffcan’t possibly be matched because it accepts only one word.
If this test is passed, then already-known-match tests for the following:
(1) The first words of the
sentargument must match the old value stored in the database. (2) The partialpatternthat remains after this placeholder must match the rest of thesentThe only significant change to longest-match is that it invokes add to compute an expanded database with the newly found match added, and it uses the resulting database as an argument to match-using-known-values.
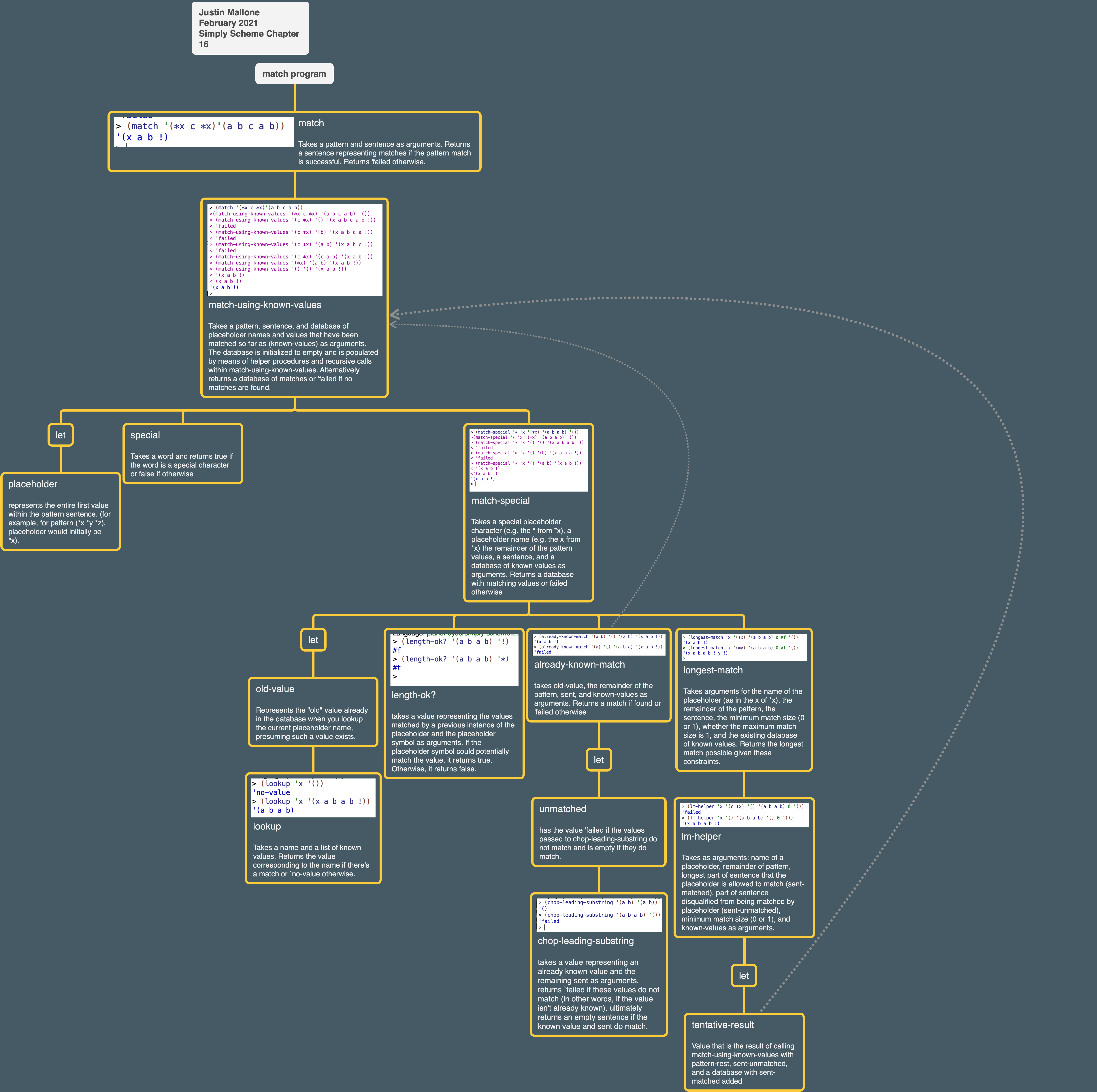
Partial Program Tree
Here’s a partial program tree I made.
Exercises about Implementation
16.8
Explain how
longest-matchhandles an empty sentence.
for longest-match, the first cond checks if sent is empty. If so, it returns true if both the following things are the case: min, which represents the minimum size of the matched text, is 0, and match? for the rest of the pattern is true. It returns false otherwise. How does this work out in practice? min will equal 0 for * and ? and 1 for ! and &. For ! and &, if we’re hitting the empty sentence without finding a match, we know we’re not returning a match, so we don’t need to worry about the possibility that those are true, which is why we only test for min being equal to 0. For * and ?, we do need to worry about the possibility of finding a match on an empty sentence, hence the call to match?.
16.9
Suppose the first cond clause in match-using-known-values were
|
1
2
|
((empty? pattern) known-values)
|
Give an example of a pattern and sentence for which the modified program would give a different result from the original.
Original:

Modified cond clause:

16.10
What happens if the sentence argument—not the pattern—contains the word * somewhere?
It seems to behave like any other word.
|
1
2
3
4
5
6
7
8
9
|
(match '(*)'(*))
;'()
(match '(*)'(* * *))
;'()
(match '(&)'(* * *))
;'()
(match '(? ?)'(* * *))
;failed
|
16.11
For each of the following examples, how many
match-using-known-valueslittle people are required?
I used trace to help me with this question.
|
1
2
|
(match '(from me to you) '(from me to you))
|

5 match-using-known-values little people for this one. The first little person gets passed the initial values from match. It goes to the ((equal? (first pattern) (first sent)) conditional and recursively invokes itself using (match-using-known-values (bf pattern) (bf sent) known-values)). This happens repeatedly until the fifth little person is handed an empty pattern, sent, and known-values. Since pattern is empty, the requirements of the first cond clause’s conditional, (empty? pattern) are met. Since sent is empty, then we return known-values per the if statement in the consequent, (if (empty? sent) known-values 'failed)). Since known-values is empty, we return the empty sentence.
|
1
2
|
(match '(*x *y *x) '(a b c a b))
|
The first match-using-known-values little person gets arguments from match and tries to match the entire sentence '(a b c a b) against *x (this is the initial “greedy” match). The program figures out (I think using already-known-match) that if it does a greedy match for the first *x it can’t have a corresponding match for the second *x, and returns 'failed. There are 3 match-using-known-values little people involved in this part of the computation.

match-using-known-values then proceeds to try matching the first *x against (a b c a) and (a b c), respectively, failing each time. There are 7 match-using-known-values little people involved in this part of the computation.

Finally, match-using-known-values attempts to match the first *x against (a b). This is successful. 5 match-using-known-values little people are involved in this stage.

So this pattern involves 15 match-using-known-values little people total.
|
1
2
|
(match '(*x *y *z) '(a b c a b))
|
This one involves 4 little people. *x greedily matches against the entire sentence, and *y and *z can match against nothing.

|
1
2
|
(match '(*x hey *y bulldog *z) '(a hey b bulldog c))
|
12 little people, with some backtracking up until the point where the procedure attempts to match *x against a. *y against b and *z against c.

|
1
2
|
(match '(*x a b c d e f) '(a b c d e f))
|
14 little people, due to an attempt at the beginning to match *x against fewer and fewer portions of the sentence before arriving at the correct solution of having *x match against nothing.

|
1
2
|
(match '(a b c d e f *x) '(a b c d e f))
|

In general, what can you say about the characteristics that make a pattern easy or hard to match?
There’s actually a slight ambiguity in the question. The standard they’re using to judge a pattern as being easy or hard to match is not obvious. Two reasonable standards could be 1) number of computational steps involved (fewer little people = easier, more little people = harder) or 2) likelihood/tendency of achieving a successful match at all (so a pattern that matches more possible sentences would be easier to match, and a pattern that matches fewer possible sentences would be harder). There is also a relationship between these two standards as described below (briefly, a pattern that matches fewer possible sentences is more likely to have to backtrack). These two standards would lead to different answers for a class of patterns where there tend to be fewer computational steps involved but the pattern will match fewer sentences. I believe such a case exists (see below). Since they just had us go through the exercise of counting up little people, I’m going to guess that they want an answer that uses number of little people as the standard, and will answer accordingly.
A pattern that has no placeholders is easy to match in terms of number of computational steps. Without placeholders there’s no need to backtrack. On the other hand, a pattern with no placeholders needs an exact match, which makes it hard to match in the sense that only one precise sequence of characters will match it.
A pattern is easy to match if the pattern’s elements are very flexible regarding what they can match. For example, '(*x *y *z) consists of elements where each element can hit on an entire group of words or no words at all. It’s not a pattern that rules much out. Because of that, it doesn’t have to do a lot of backtracking to find an acceptable pattern after hitting an unacceptable one.
'(*x *y *x) isn’t an example of a pattern where each element is flexible. This is because the final element is a duplicate of the first, which greatly constrains the sentences that might match this pattern.
A placeholder earlier in the pattern can involve more computational steps than a placeholder later in the pattern. This is because a “greedy” placeholder match has more potential matches to consider earlier on than later on. Compare, for example, '(*x a b c d e f) to (a b c d e f *x) above.
16.12
Show a pattern with the following two properties: (1) It has at least two placeholders. (2) When you match it against any sentence, every invocation of
lookupreturnsno-value.
My intuition is that if we have at least two placeholders in our pattern, there is going to be some sentence that matches the pattern. So we don’t want to try to create a pattern that doesn’t match on a sentence. Instead, we want to create a pattern that returns no-value for every invocation of lookup but matches on a sentence anyways.
Let’s step through lookup so we know something about how it actually works before we try to answer this question. Something to note is that lookup only gets invoked in match-special and itself. That’s part of the reason we have the restriction in the problem statement of having to have placeholders – because if we didn’t, then lookup wouldn’t get invoked at all, and then we wouldn’t have to say anything about it.
|
1
2
3
4
5
6
|
(define (lookup name known-values)
(cond ((empty? known-values) 'no-value)
((equal? (first known-values) name)
(get-value (bf known-values)))
(else (lookup name (skip-value known-values)))))
|
First cond: if known-values is empty, we return 'no-value.
Second cond: If the first value of known-values is equal to name, we invoke get-value on the all but the first of known-values.
Otherwise (else), we recursively call lookup with name and a procedure skip-value which is passed known-values as an argument.
So lookup is only going to return 'no-value when known-values is empty. When is known-values going to be empty? See below.
Let’s consider skip-value before moving on to looking at a specific example:
|
1
2
3
4
5
|
(define (skip-value stuff)
(if (equal? (first stuff) '!)
(bf stuff)
(skip-value (bf stuff))))
|
If the first value of stuff is !, then skip-value will return bf stuff. Otherwise, it recursively calls itself with bf stuff. So it basically keeps going through stuff until it hits a !, at which point lookup tries to find a match again at the point just past the !.
Let’s look at a specific example.
(match '(*x *y) '(a b a b))

x gets passed to lookup but there aren’t any known-values yet so it returns no-value as you might expect.
Then, we provisionally match *x against the entire sentence, and then do a lookup for y. This is the interesting part for our question. y doesn’t match the x. At this point, skip-value kicks in and starts moving through the remainder of known-values. Ultimately, we wind up with an empty known-values sentence, because we haven’t found a match. lookup tries to look y up in this empty sentence, but of course fails. So we return no-value for this case as well.
But ultimately, we do get a match despite returning no-value for every instance of lookup, because the program matches *x against the entire initial sentence and *y against nothing.
Note that if we’d had the same placeholder, as in (match '(*x *x) '(a b a b)), we would have gotten matches for lookup instead of no-value.

So what conclusions can we draw from all this? I think we can say that if we have two * placeholders with different names (as in *x and *y), we will return no-value for each instance of lookup (since lookupwon’t find a match for the different names).
16.13
Show a pattern and a sentence that can be used as arguments to match so that lookup returns (the beatles) at some point during the match.
The Simply Scheme guys really like the Beatles.
|
1
2
|
(match '(*x *x) '(the beatles the beatles))
|
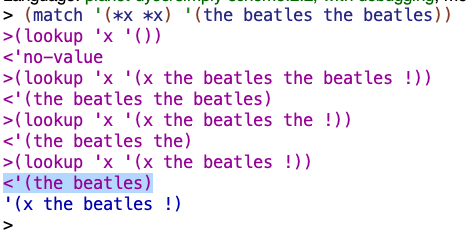
16.14
Our program can still match patterns with unnamed placeholders. How would it affect the operation of the program if these unnamed placeholders were added to the database?
Well, for example, for input like (match '(* *) '(the beatles the beatles)) we might expect to get a return value like '(* the beatles !), paralleling the '(x the beatles !) we get for (match '(*x *x) '(the beatles the beatles)). Instead, for (match '(* *) '(the beatles the beatles)) we get an empty sentence.
What part of the program keeps them from being added?
match-using-known-values and add are the key procedures. match-using-known-values assumes that placeholders are going to be named and therefore tries to pull apart the placeholder and the name for the placeholder when it passes values to match-special. This results in unnamed placeholders having an empty word for the name value of match-special, which ultimately flows down through the procedure until arriving at add. Add wants a name in order to add something to the database – otherwise add just returns known-values instead of adding an entry by running the (se known-values name value '!) line.
16.15
Why don’t
get-valueandskip-valuecheck for an empty argument as the base case?
lookup itself handles the case of an empty known-values, and known-values is the same thing that gets passed as an argument (in some form) to get-value and skip-value. Basically, neither get-value or skip-value have to worry about the empty case because they’re just helper procedures that help lookup with specialized tasks. More details below.
skip-value isn’t a self-sufficient recursive procedure. It’s job is to work with together with lookup and specifically to move to the point in known-values at which the next entry in the database in known-values begins. This is to handle the case where the name of a placeholder being looked up differs from the name of the current entry in the database. e.g. if you’re trying to lookup the value for y but the next database entry is a sentence for x:

The base case for skip-value is ! because that’s the value that demarcates a new database entry. lookup itself handles the case of an empty known-values, so that case is still covered.
Like skip-value, get-value works with lookup, and lookup handles the case of an empty known-values. get-value does a different job than skip-value, in that get-value retrieves the value for a match holding placeholder name rather than skipping the value of a non-matching name:

16.16
Why didn’t we write the first
condclause inlength-ok?as the following?
|
1
2
|
((and (empty? value) (member? howmany '(? *))) #t)
|
So the existing first cond clause is:
|
1
2
|
((empty? value) (member? howmany '(? *)))
|
With (match '(*x !x)'(a b a b)) the existing code runs fine:

With the proposed code, this happens:


With the original code, the case where value is empty gets handled by the first cond clause, since an empty value fully passes the (empty? value) conditional. Since ! isn’t a member of '(? *), length-ok? returns false.
With the new code, the case where value is empty does not get handled by the first cond clause, since the new condition requires meeting both the (empty? value) and (member? howmany '(? *)) tests, and a call to length-ok? where the value for howmany is ! will fail to meet the latter. Thus, the same case that was handled by the first cond clause in the original code instead winds up getting handled by the second cond clause, ((not (empty? (bf value))) (member? howmany '(* &))). As we’ve seen many times, taking bf of something empty leads to an error.
So we didn’t write it the way the authors suggest in order to avoid this error.
16.17
Where in the program is the initial empty database of known values established?
The very first part of the program:
|
1
2
3
|
(define (match pattern sent)
(match-using-known-values pattern sent '()))
|
The empty sentence being passed to match-using-known-values becomes known-values, which is the database.
16.18
For the case of matching a placeholder name that’s already been matched in this pattern, we said on page there that three conditions must be checked. For each of the three, give a pattern and sentence that the program would incorrectly match if the condition were not checked.
The three conditions were:
1) The first words of the
sentargument must match the old value stored in the database. (2) The partialpatternthat remains after this placeholder must match the rest of thesent. (3) The old value must be consistent with the number of words permitted by thehowmanypart of the placeholder.
The old value must be consistent with the number of words permitted by the howmany part of the placeholder.
Context
[The] third condition is actually checked first, by
length-ok?, and if we pass that hurdle, the other two conditions are checked byalready-known-match.
Some procedure code for context:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
|
(define (match-special howmany name pattern-rest sent known-values)
(let ((old-value (lookup name known-values)))
(cond ((not (equal? old-value 'no-value))
(if (length-ok? old-value howmany)
(already-known-match
old-value pattern-rest sent known-values)
'failed))
((equal? howmany '?)
(longest-match name pattern-rest sent 0 #t known-values))
((equal? howmany '!)
(longest-match name pattern-rest sent 1 #t known-values))
((equal? howmany '*)
(longest-match name pattern-rest sent 0 #f known-values))
((equal? howmany '&)
(longest-match name pattern-rest sent 1 #f known-values)))))
|
|
1
2
3
4
5
|
(define (length-ok? value howmany)
(cond ((empty? value) (member? howmany '(? *)))
((not (empty? (bf value))) (member? howmany '(* &)))
(else #t)))
|
A bunch of analysis as necessary context:
match-specialdefines old-value using lookup invoked with the placeholder name (for example, the twice part of the expression!twice when using !twice as a pattern) and known-values. old-value represents the values matched by a previous instance of the placeholder. length-ok? uses old-value and howmany (howmany representing the special character at the start of a placeholder – the ! from !twice, for instance) to see if old-value is consistent with the howmany part of the placeholder.
For example, if the pattern is
|
1
2
|
(*stuff and !stuff)
|
and the database says that the placeholder
*stuffwas matched by three words from the sentence, then the second placeholder!stuffcan’t possibly be matched because it accepts only one word.
So the way length-ok? actually works in detail in a case like this is this: first, it checks whether or not the database match for *stuff is empty. If so, it evaluates whether the ! from !stuff is a member of '(? *) and returns the appropriate truth value. * can match on any number of words, including none, and ? can match on at most one word, including none, so these are the only two symbols that can be empty, which is why we are testing for them. If value were empty but the placeholder being checked were !, which requires precisely 1 word, or &, which requires at least one word, then we would know that we can’t have a match with that placeholder, and so length-ok? should return #f.
If the first cond line is not evaluated, length-ok? evaluates whether bf value is not empty. if so, it evaluates (member? howmany '(* &) and returns the appropriate boolean. The bf of a value not being empty means that that value has at least two words (since if value just had 1 word then bf value would be empty!). * and & can match 2 (or more) words – ! and ? cannot. So we test the placeholder for membership in the sentence '(* &) on the second cond line. If it is instead ! or ?, it should return false.
If neither cond is meant, length-ok? returns true.
So, step by step with an example:

The bf of (a b a b) is not empty (so we evaluate the second cond line), but ! isn’t a member of '(* &), so we return #f. This makes sense, since ! can only match on exactly one word, but is trying to match on 4.

Similar result as before.
![]()
(a) is not empty, so this fails the first cond. bf of '(a) is empty, so this doesn’t meet the second cond line’s conditional either. We return #t. This makes sense. A one-sentence word is indeed acceptable for !, which matches on exactly one word 🙂
![]()
'() is empty, so we evaluate the first cond clause. ! isn’t a member of '(* &), so we return false. This makes sense. ! requires exactly one word, and we’re trying to match it to the empty sentence.
Ultimately, (match '(*x !x)'(a b a b)) returns 'failed.
Answer
So let’s back up to the prompt, which was to “give a pattern and sentence that the program would incorrectly match if the condition were not checked.” And let’s recall that the condition we’re checking is that “[t]he old value must be consistent with the number of words permitted by the howmany part of the placeholder.” Let’s comment out the parts of length-ok? that perform these checks so that length-ok? always returns true, which amounts to not checking for the condition being met and just assuming that it’s true.
|
1
2
3
4
5
|
(define (length-ok? value howmany)
(cond ;((empty? value) (member? howmany '(? *))) ; commented out
;((not (empty? (bf value))) (member? howmany '(* &))) ; commented out
(else #t)))
|
We know that (match '(*x !x)'(a b a b)) returns 'failed with the normal program. What about with the modified one?

Without checking for whether or not the length of value is okay given the placeholder, the procedure erroneously thinks that it’s found a match for the !x in the form of the second a b when it sees that there’s a '(x a b !)) entry in the database.
The first words of the sent argument must match the old value stored in the database.
Context
Ok onto our next condition. Some necessary procedure code and analysis follows. Keep in mind that value in already-known-match represents the old value stored in the database.
|
1
2
3
4
5
6
7
|
(define (already-known-match value pattern-rest sent known-values)
(let ((unmatched (chop-leading-substring value sent)))
(if (not (equal? unmatched 'failed))
(match-using-known-values pattern-rest unmatched known-values)
'failed)))
|
If unmatched, whose value derives from chop-leading-substring, which is described in detail below, returns some value other than 'failed, then that value is passed to match-using-known-values as the sent to match any remaining patterns against. Otherwise, 'failed is returned.
|
1
2
3
4
5
6
7
|
(define (chop-leading-substring value sent)
(cond ((empty? value) sent)
((empty? sent) 'failed)
((equal? (first value) (first sent))
(chop-leading-substring (bf value) (bf sent)))
(else 'failed)))
|
chop-leading-substring is a recursive procedure. If value is empty, it returns sent. This is the base case that occurs, for example, when an identical value and sent have been provided to chop-leading-substring and the procedure made recursive calls until running out of both value and sent at the same time. If, on the other hand, the procedure runs out of sent before running out of value, it returns 'failed. In this case, the old value from the database apparently did not match the sent argument, since there is value remaining but sent is empty, and so returning 'failed is appropriate. If the first words from both value and sent are equal, then the procedure recursively calls itself with the bf of both those respective values. Finally, in the only remaining alternative, where there are still value and sent remaining but the first of both those respective sentences do not match, we return failed, which makes sense.
So consider the case of (match '(*x *x)'(a b a b)). Let’s go step by step:

We’re trying to match the first *x against the entire sentence (the greediest match). sent is empty in chop-leading-substring, so we should expect (and get) failed, which triggers another failed in already-known-match.

another failed.

Now something interesting happens. the value and sent values match for chop-leading-substring. the procedure recursively does bf through them until arriving at empty values, and then returns the empty sent when running its cond clause ((empty? value) sent). Since this is not failed, already-known-match sends the empty sent as the sent to match any remaining patterns against.

Answer
So with the above in mind, we can proceed to edit chop-leading-substring in such a way as to not check that the first words of the sent argument are equal the old value stored in the database.
Here’s my edit:
|
1
2
3
4
5
6
7
|
(define (chop-leading-substring value sent)
(cond ((empty? value) sent)
((empty? sent) sent)
((equal? (first value) (first sent))
(chop-leading-substring (bf value) (bf sent)))
(else 'failed)))
|
This returns sent even when value is not empty but sent is (that is to say, when value and sent don’t match.
And let’s see what happens with (match '(*x *x)'(a b a b).

What I think is the most important line is highlighted. Before, for this line, we returned 'failed. Now what’s happening? This first chain of calls is a provisionally “greedy” grab that is trying to match the whole sentence against the first *x. In a correctly functioning program, we don’t want that to happen because we want there to be “enough” sentence left over for the second *x. However, when chop-leading-substring returns an empty sentence instead of 'failed, that empty sentence is passed to match-using-known-values, along with an empty pattern value and, critically, a database representing a match of the whole sentence against the first *x. Empty pattern + empty sentence is the condition under which match-using-known-values returns known-values, so our provisional database matching the entire sentence against the first *x is incorrectly returned as the result.
The partial pattern that remains after this placeholder must match the rest of the sent.
Consider the following expression:
|
1
2
|
(match '(*x *x *x *y *x)'(a b a b a b c d a b))
|
This is how it matches with a functioning program:
![]()
Now imagine that we rewrite already-known-match to remove the call to match-using-known-values that checks the remaining part of the pattern against the unmatched portion of the sentence, and just return known-values if unmatched is not equal to failed, like so:
|
1
2
3
4
5
6
|
(define (already-known-match value pattern-rest sent known-values)
(let ((unmatched (chop-leading-substring value sent)))
(if (not (equal? unmatched 'failed))
known-values
'failed)))
|
What happens?
![]()
We lose the match information for *y!
16.19
What will the following example do?
|
1
2
|
(match '(?x is *y !x) '(! is an exclamation point !))
|
It fails.
![]()
Can you suggest a way to fix this problem?
Yes!
I think the problem must be caused by using the exclamation point in this program in two roles – as a separator of database entries and as a special character/placeholder. So I changed the separator in get-value, skip-value and add to a † instead of a !:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
|
(define (get-value stuff)
(if (equal? (first stuff) '†)
'()
(se (first stuff) (get-value (bf stuff)))))
(define (skip-value stuff)
(if (equal? (first stuff) '†)
(bf stuff)
(skip-value (bf stuff))))
(define (add name value known-values)
(if (empty? name)
known-values
(se known-values name value '†)))
|
With these changes:

🙂
The ?x matches on the the first ! and the !x on the final one. The match for “is” doesn’t show up in the result, as expected. The *y matches on the remaining words.
BTW I initially tried using the vertical bar as a separator but DrRacket didn’t seem to like that.
❌ 16.20
Modify the pattern matcher so that a placeholder of the form
*15xis like*xexcept that it can be matched only by exactly 15 words.
|
1
2
3
4
|
> (match '(*3front *back) '(your mother should know))
(FRONT YOUR MOTHER SHOULD ! BACK KNOW !)
|
Couldn’t figure this one out.
Here was my first attempt. Basically what I was trying to do was break up match into a “star-number” call (the part with the *3* or whatever at the beginning of the placeholder) and the “regular” part of the match, and stitch them together at the end:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
|
(define (bln n)
(repeated bl n))
(define (bfn n)
(repeated bf n))
(define (star-number? pattern)
(if (and (> (count pattern) 0)
(> (count (first pattern)) 1)
(equal? (first (first pattern))'*)
(number? (first (bf (first pattern)))))
(first (bf (first pattern)))
#f))
(define (match pattern sent)
(cond ((star-number? pattern)
(let ((exactnum (star-number? pattern)))
(if (<= exactnum (count sent))
(se (match (se (word (first (first pattern)) (bf (bf (first pattern)))))
((bln (- (count sent) exactnum)) sent))
(match (bf pattern)((bfn exactnum) sent)))
'failed)))
(else (match-using-known-values pattern sent '()))))
|
I had some limited success with this approach:

But it was indeed limited:

I tried some other things as well but couldn’t figure the problem out.
16.21
Modify the pattern matcher so that a
+placeholder (with or without a name attached) matches only a number:
|
1
2
3
4
|
> (match '(*front +middle *back) '(four score and 7 years ago))
(FRONT FOUR SCORE AND ! MIDDLE 7 ! BACK YEARS AGO !)
|
The
+placeholder is otherwise like!-it must match exactly one word.
First thing I did was add + to the list of characters in special?
|
1
2
3
|
(define (special? wd)
(member? (first wd) '(* & ? ! +)))
|
The second thing I did was add something to handle + in match-special.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
|
(define (match-special howmany name pattern-rest sent known-values)
(let ((old-value (lookup name known-values)))
(cond ((not (equal? old-value 'no-value))
(if (length-ok? old-value howmany)
(already-known-match
old-value pattern-rest sent known-values)
'failed))
((equal? howmany '?)
(longest-match name pattern-rest sent 0 #t known-values))
((equal? howmany '+)
(if (and (not (empty? sent))
(number? (first sent)))
(longest-match name pattern-rest sent 1 #t known-values)
'failed))
((equal? howmany '!)
(longest-match name pattern-rest sent 1 #t known-values))
((equal? howmany '*)
(longest-match name pattern-rest sent 0 #f known-values))
((equal? howmany '&)
(longest-match name pattern-rest sent 1 #f known-values)))))
|
I put (not (empty? sent)) in there to make sure that my new code didn’t try to grab the first of an empty sentence. The (number? (first sent)) is of course to check whether the first value of the sentence is a number in the case where the + is the placeholder we are considering. The longest-match arguments are the same as ! under the theory that we want it to behave like ! other than only matching a number.
Some tests:

Looks good.