set?
Based on what they say in the book, I’m guessing that a set is defined as a list of atoms where no atom appears more than once. This includes the empty set.
This was my solution:
|
1
2
3
4
5
6
|
(define myset?
(lambda (lat)
(cond ((null? lat) #t)
((> (occur (car lat) lat) 1) #f)
(else (myset? (cdr lat))))))
|
This was their solution:

Their way is very similar to mine. The main difference is that I used occur for my second line to see whether there was more than 1 occurrence of the first element of the list within the entire list. So with the example (apple peaches apple plum), I’d check if apple occurred more than once. Since it does, I return false. With their approach, they check if the first element of the list is a member of the remainder of the list. So with the same example, they’d check if apple was a member of (peaches apple plum). Since it is, that indicates there are two copies of apple, and so they return false. I think both approaches are fine.
makeset

![]()
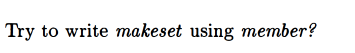
I tried but made an error:
|
1
2
3
4
5
6
7
8
9
|
(define mymakeset
(lambda (lat)
(cond
((null? lat) '())
((member? (car lat) (cdr lat))
(mymakeset (cdr lat)))
(else (cons (car lat)
(mymakeset (cdr lat)))))))
|

The output should be

The way I wrote my member? line, the first copy of an atom in a list is being thrown out, but I actually want the second copy to be the one that isn’t included.
I figured out how to get the result I wanted with the following approach:
|
1
2
3
4
5
6
7
8
|
(define mymakeset
(lambda (lat)
(cond
((null? lat) '())
((member? (car lat) (cdr lat))
(cons (car lat) (mymakeset (rember* (car lat) (cdr lat)))))
(else (cons (car lat) (mymakeset (cdr lat)))))))
|
This is similar to the earlier approach in some ways. The key difference is the use of the rember* procedure to remove all subsequent instances of an atom from a list.
They want to use multirember instead of rember*.
They also made things shorter:

With the previous way of solving the problem, we cared whether car lat was a member of cdr lat because we only wanted to “skip” consing the first element of the lat together with the rest of the list when that first element was in fact a member of the rest of the list. But with multirember, we can just call it for each car lat recursively. If there are no duplicates, then multirember just returns the whole second argument that it’s given. There’s no downside to just using it every time.
subset?
They ask for a procedure that checks whether one set is a subset of another set, and they define that as each element of the first set appearing somewhere in the second set. My solution:
|
1
2
3
4
5
6
7
|
(define mysubset?
(lambda (set1 set2)
(cond ((null? set1) #t)
((member? (car set1) set2)
(mysubset? (cdr set1) set2))
(else #f))))
|
Their shortened version of the procedure was exactly the same:

Next question:
![]()
This was my solution:
|
1
2
3
4
5
6
|
(define mysubset2?
(lambda (set1 set2)
(cond ((null? set1) #t)
(else (and (member? (car set1) set2)
(mysubset2? (cdr set1) set2))))))
|
Their solution was the same.
eqset?

They want you to write eqset?. My attempt:
|
1
2
3
4
5
6
7
8
|
(define myeqset?
(lambda (set1 set2)
(cond
((and (null? set1) (null? set2)) #t)
((member? (car set1) set2)
(myeqset? (cdr set1) (rember (car set1) set2)))
(else #f))))
|
I check if both sets are empty to make sure they have the same number of atoms.
If car set1 is a member of set2, I recursively call myeqset? with the remainder of set1 and a version of set2 with the first instance of the value of set1 removed by rember. Otherwise, I return false.
A similar simplification as was used in the subset procedure is possible here by using and:
|
1
2
3
4
5
6
7
|
(define myeqset?
(lambda (set1 set2)
(cond
((and (null? set1) (null? set2)) #t)
(else (and (member? (car set1) set2)
(myeqset? (cdr set1) (rember (car set1) set2)))))))
|
They had a different approach:

I like this approach and find it elegant.
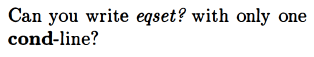
I was not sure quite what they were getting at. It was apparently this:

A shorter version (that they agree with):
|
1
2
3
4
5
|
(define myeqset2?
(lambda (set1 set2)
(and (subset? set1 set2)
(subset? set2 set1))))
|
intersect?
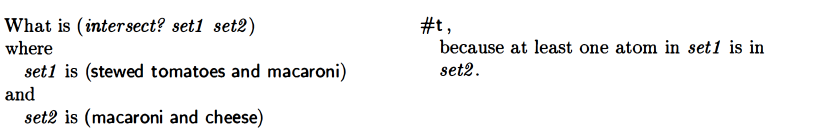
![]()
My attempt:
|
1
2
3
4
5
6
7
|
(define myintersect?
(lambda (set1 set2)
(cond
((null? set1) #f)
((member? (car set1) set2) #t)
(else (myintersect? (cdr set1) set2)))))
|
This was the same as their shorter version.
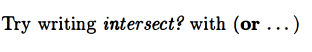
|
1
2
3
4
5
6
7
|
(define myintersect2?
(lambda (set1 set2)
(cond
((null? set1) #f)
(else (or (member? (car set1) set2))
(myintersect? (cdr set1) set2)))))
|
Their version was the same.
intersect

![]()
My attempt:
|
1
2
3
4
5
6
7
8
|
(define myintersect
(lambda (set1 set2)
(cond
((null? set1) '())
((member? (car set1) set2)
(cons (car set1) (myintersect (cdr set1) set2)))
(else (myintersect (cdr set1) set2)))))
|
Their version agrees with mine.
union
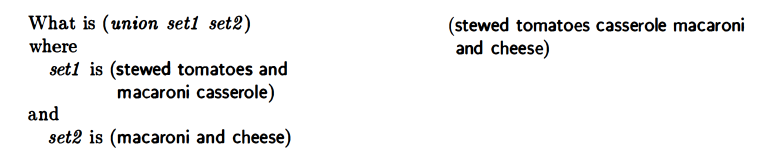
My answer:
|
1
2
3
4
5
6
7
8
|
(define myunion
(lambda (set1 set2)
(cond
((null? set1) set2)
((member? (car set1) set2)
(myunion (cdr set1) set2))
(else (cons (car set1) (myunion (cdr set1) set2))))))
|
Their solution was the same.
mystery function

It returns elements that are unique to set 1. It is very similar to union. The base case is different, though. Instead of returning the entirety of set2 like in union, this program returns the empty list. Since xxx skips over any elements from set1 that appear in set2, and only conses elements onto the new list it builds which appear only in set1 and not in set2, returning the empty list when set1 is null leads to a list being generated of only the items that are unique to set1.

intersectall
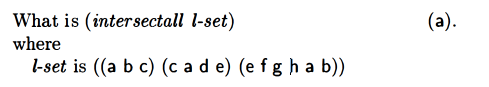


Wasn’t sure how to proceed on this one.

Gonna walk through the first example with the lists of letters in order to understand what’s happening here.
So the base case would be when we have one list left, (e f g h a b). That’s when cdr l-set would be null. In that case, we return '(e f g h a b).
So one recursive “step up”, we’d find the intersect of (c a d e) and (e f g h a b), which would be (a e). Then that value would be returned as the result of intersectall one further recursive step up, and so we’d then find the intersect of (a b c) and (a e), which is (a).
a-pair?

Here was my initial mistaken attempt at defining a-pair?:
|
1
2
3
4
5
|
(define my-a-pair?
(lambda (l)
(null? (cdr (cdr l)))))
|
I only caught one of the cases though:

If you give a-pair? a single atom (like 3), or the empty list, or an empty nested list (()), my version returns an error message, whereas their version appropriately returns false.
one-liners of pair functions

One-liners:
|
1
2
3
4
5
6
7
8
9
10
11
12
|
(define first
(lambda (p)
(car p)))
(define second
(lambda (p)
(car (cdr p))))
(define build
(lambda (s1 s2)
(cons s1 (cons s2 '()))))
|
![]()
My answer:
|
1
2
3
4
5
|
(define third
(lambda (p)
(car (cdr (cdr p)))))
|
rels and fun?

I’m not sure why the example with the question mark added isn’t a rel. It seems like it should be considered a rel, as it seems like a set of pairs.
Ok I think I figured it out. A rel is a list of pairs that is a set. A set is a list in which no value appears more than once. Since apples peaches appears more than once in the list I wasn’t sure about, that list isn’t a rel. A value can appear as part of a pair more than once (for example, the number 4 appearing more than once in a list) and the list can still be a rel, as long as the full entry isn’t duplicated (e.g. as long as (4 2) doesn’t appear twice).

a function for our purposes is a rel for which no first value in a pair appears more than once.
![]()
My attempt:
|
1
2
3
4
|
(define myfun?
(lambda (rel)
(set? (firsts rel))))
|
They agree.
revrel
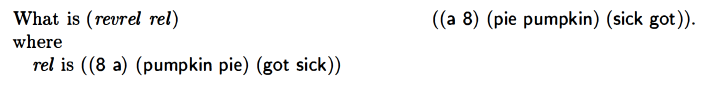
|
1
2
3
4
5
6
7
8
9
|
(define myrevrel
(lambda (rel)
(cond ((null? rel)'())
(else (cons (cons
(car (cdr (car rel)))
(cons (car (car rel)) '()))
(myrevrel (cdr rel))
)))))
|
Their version was cleaner.

They also did my version, but they maintain that their version is more readable. I agree.

My solution:
|
1
2
3
4
5
6
7
|
(define myrevrel
(lambda (rel)
(cond ((null? rel)'())
(else (cons (myrevpair (car rel))
(myrevrel (cdr rel))
)))))
|
Their solution was the same.
fullfun?
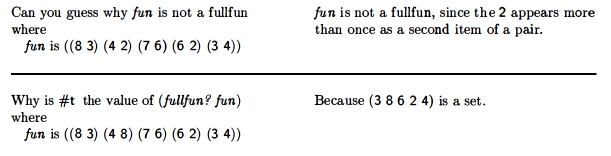
So they want you to write fullfun?. I discovered that seconds was a function while doing this.
|
1
2
3
4
|
(define myfullfun?
(lambda (fun)
(set? (seconds fun))))
|
They agreed 🙂
seconds
They want you to define seconds.
My approach:
|
1
2
3
4
5
6
7
|
(define myseconds
(lambda (l)
(cond ((null? (cdr l))
(cdr (car l)))
(else (cons (second (car l))
(myseconds (cdr l)))))))
|
We cons the second value of the first pair/sublist onto the value of the recursive call to myseconds with the rest of l. Then when we get to the case where there’s only one pair left, we get the cdr (car l) of that list, which returns the second value as a list. We actually want it as a list so we can cons onto it.
