Getting Started
This chapter has us start off by loading a “functions.scm” file which can be downloaded here. You want to load the file by typing (load "functions.scm") in the Interactions window of DrRacket, and not in the Definitions window. If you try loading it in Definitions window, you may get an error message like I did.
Once the file is loaded, the program does not automatically start; you need to type (functions) to start the program. The functions program creates a special way of entering functions that is different than the normal way that scheme operates. It gives you a prompt to enter a function and then prompts you to enter arguments. The number of arguments you can enter varies. For example, sqrt only lets you enter one argument, which makes sense. OTOH, + and se let you enter two arguments. It’s worth noting that the number of arguments does not necessarily correspond to what the “real” Scheme function lets you enter – for instance, you can enter (+ 1 2 3 4 5 6) in Scheme no problem and get an answer, but the functions program does not let you do that. You can exit the functions.scm program by typing exit instead of typing the name of a function.
Playing With Functions
Math Functions
I tried performing some of the operations suggested by the chapter:

If I enter 1 ÷ 987654321987654321 in a calculator program, I get this

So I was expecting something similar to that for the / function.
The math functions don’t like words:

Some playing around with the odd? function, which tests whether a number is odd. Note the message related to not being in the domain for the argument 3.5.

remainder
Remainder:
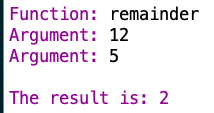
A book-suggested example:
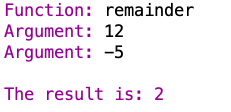
another example:
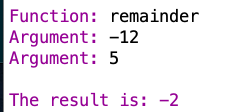
And another:

The sign of the result is the same as the sign of the first argument, which is the dividend. So I think remainder gives the remainder that results when both arguments are non-negative, and then makes the remainder negative if the first argument is negative.
Yeah this seems to be the case.
The remainder function doesn’t seem to like decimals:

expt
The book says:
Some two-argument functions have complicated domains because the acceptable values for one argument depend on the specific value used for the other one. (The function expt is an example; make sure you’ve tried both positive and negative numbers, and fractional as well as whole-number powers.)
Some experiments with expt
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
|
Function: expt
Argument: 2
Argument: 2
The result is: 4
Function: expt
Argument: 2
Argument: -2
The result is: 1/4
Function: expt
Argument: 2
Argument: -1/2
The result is: 0.7071067811865476
Function: expt
Argument: -2
Argument: 3
The result is: -8
Function: expt
Argument: -2
Argument: -1/2
Argument(s) not in domain.
Function: expt
Argument: -1/2
Argument: 1/3
The result is: 0.39685026299205+0.6873648184993013i
Function: expt
Argument: 2
Argument: 0
The result is: 1
Function: expt
Argument: 0
Argument: -1
. . definitions/simply_redef.scm:813:29: expt: undefined for 0 and -1
|
So you can see that with -2 and -1/2 as arguments I managed to get something that was outside the domain.
AnneB says:
I think the domain rule for expt is:
- the first argument can be any real number
- if the first argument is positive, the second argument can be any real number
- if the first argument is 0, the second argument can be a non-negative real number
- if the first argument is negative, then the second argument can be 0 or it can be a real number with absolute value greater than or equal to 1
Let’s try some more, with an eye towards seeing if AnneB is right!
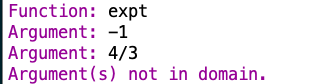
That’s a negative number for the first argument, and a real number with an absolute value greater than 1 for the second argument, but this set of arguments appears to not be in the domain. So that appears to contradict AnneB’s final claim re: domain (though I could be wrong).
If the first argument is negative, it doesn’t seem like the expt function treats fraction or decimal values for the second argument as being within the domain. You can enter negative integer numbers for the second value, though (along with 0 and positive integers). So it is possible that Anne’s final claim should be redrafted as: “if the first argument is negative, then the second argument can be any integer.”
Rounding Mystery 🔍🧐
Another book example:
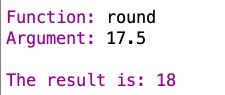
This is the result of my playing with the round function a bit:
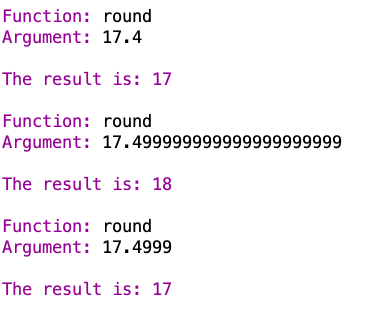
Very interesting. So at some point in between 17.4999 and 17.499999999999999999999 something happens. My wild guess is that DrRacket/Scheme only keeps track of numbers to a certain level of precision regardless of how many digits you enter, and then rounds the number off internally (to whatever level of precision it keeps track of the numbers), and that if use a number that happens to be long enough to run into this issue and then try to feed that number into a function that rounds the number off, you basically get two levels of rounding, leading to the result of 17.499999999999999999999 getting rounded off to 18.
Hey I thought of a way to test this. Since Scheme returns the number you give it back to you, if what I’m saying is actually true, then normal Scheme should give me back a rounded-off number once I hit a certain number of digits.
Let’s see 🖥🧐
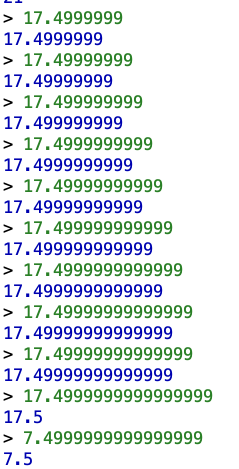
Yep. It looks like it’ll do 14 digits of precision after the decimal point, but once it hits that 15th digit, Scheme is like “nah” and rounds the number off to 17.5. And the final line there is just testing to make sure the threshold is digits after the decimal point (which it appears to be).
I vaguely remember running into an issue like this before in a previous run through Scheme or SICP or something. Maybe I’ll come across it as a I review my old work.
Word Functions
Some more book suggestions:
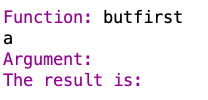
butfirst returns all but the first letter of a word. So if you give it a one-letter word, you get nothing. But if you give it a multi-letter word:

butfirst treats numbers in the same way it treats words:
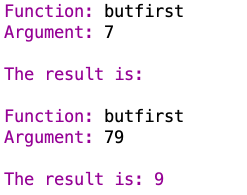
and first behaves similarly

butfirst won’t count arguments with multiple words in them:
![]()
![]()
![]()

Apparently the following version is supposed to work:
![]()
But I and other people are having trouble with the functions.scm functions not accepting sentences in our versions of Scheme.
word takes 2 arguments and doesn’t respect spaces:

And you can’t use quotes (this seems to be true in general for the functions in functions.scm)
Whereas in the normal Scheme version of word, you can use spaces by putting a word in quotes and having a space at the end or by quoting a space separately:

both functions.scm word and normal Scheme word treat numbers as strings of characters:

![]()
Count
Now onto count:
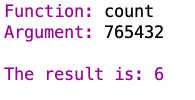
count is counting up the number of digits in the argument you give it, and it does that for sequences of numbers as well as for words.
The regular Scheme version of count handles this numerical sequence the same way:
![]()
count doesn’t like spaces in words:

count could conceivably just treat the whole thing as a third-character sequence, one of which is a space, but it doesn’t.
The normal Scheme version of count handles this situation differently than the functions.scm count. It thinks the “United” is trying to refer to some definition for “United” that it can’t find:

Normal scheme count has the same behavior just for “United”

whereas the functions.scm count can handle “United” by itself and produce the result that you would expect:

Normal Scheme count can, of course, deal with “United” if you indicate that it is a word/string by putting a ‘ mark before the “United”:

Whereas the functions version of count actually treats a ‘ as part of the sequence of characters that it attempts to count up:

Ifs and Booleans
if takes 3 arguments:


If the first argument returns true, then the second argument gets returned. If the first argument returns false, then the third argument gets returned.
Functions
The book provides some examples of functions that take other functions:
|
1
2
3
4
5
|
Function: number-of-arguments
Argument: equal?
The result is: 2
|
The range of number-of-arguments is nonnegative integers. But its domain is functions. For example, try using it as an argument to itself!
Heh okay.

As expected 🙂
If you’ve used other computer programming languages, it may seem strange to use a function—that is, a part of a computer program—as data. Most languages make a sharp distinction between program and data. We’ll soon see that the ability to treat functions as data helps make Scheme programming very powerful and convenient.
Ah okay, so this is a notable feature of Scheme in particular.
The book suggests trying this example:
|
1
2
3
4
|
Function: keep
Argument: vowel?
Argument: constantinople
|

So the keep function is taking the vowel? function and a word as arguments and keeping the vowels.
Another example of this kind of thing:

Some functions that take other functions aren’t defined in the functions program:

Domain and Range
Simply Scheme Chapter 2 says:
So far most of our functions fall into one of two categories: the arithmetic functions, which require numbers as arguments and return a number as the result; and the word functions, which accept words as arguments and return a word as the result. The one exception we’ve seen is
count. What kind of argument doescountaccept? What kind of value does it return? The technical term for “a kind of data” is a type.
count takes strings of characters (could be letters, numbers, both) which we might call a “word” and returns a number.
The technical term for “the things that a function accepts as an argument” is the domain of the function. The name for “the things that a function returns” is its range. So the domain of
countis words, and the range ofcountis numbers (in fact, nonnegative integers). This example shows that the range may not be exactly one of our standard data types; there is no “nonnegative integer” type in Scheme.
Right okay. A function’s range doesn’t have to be something Scheme knows about.
How do you talk about the domain and range of a function? You could say, for example, “The cos function has numbers as its domain and numbers between −1 and 1 as its range.” Or, informally, you may also say “Cos takes a number as its argument and returns a number between −1 and 1.”[3]
For functions of two or more arguments, the language is a little less straightforward. The informal version still works: “Remainder takes two integers as arguments and returns an integer.” But you can’t say “The domain of remainder is two integers,” because the domain of a function is the set of all possible arguments, not just a statement about the characteristics of legal arguments.[4]
Yeah okay that makes sense. For example, the regular Scheme version of + can take no arguments or a ton of arguments. You can’t say “the domain of + is two arguments” just because 2 is a permissible number of arguments. The domain is supposed to be a generally true statement about the things that a function accepts as an argument.
I am getting “Argument(s) not in domain.” errors when I’m not supposed to when a sentence is an argument. I haven’t figured out how to resolve this as of yet. Fortunately, the issue appears to only affect the functions.scm functions and that file is only used for Chapter 2, so I don’t think this is a huge deal.
Exercises
Use the
functionsprogram for all these exercises.
For some of these, I ran into the problem with sentences not being in the domain of functions.scm functions, so I tested them out in regular Scheme. I had to define vowel? in regular Scheme – for that, I just stole code from Chapter 8.
For the purpose of answering these questions, i’m going to assume that if a function takes a number as an argument but treats it like a word, that the type of the number-as-word counts as “word” and not “number.”
Also, the data types I’m focusing on in my answers are words, numbers, booleans, and functions. I don’t care so much about data subtypes like “positive integers” though I may mention them. Sentence-handling is a bit broken in the functions used in this chapter, as mentioned above.
Exercise 2.1
In each line of the following table we’ve left out one piece of information. Fill in the missing details.
I just made up a word for the eieio line 🙂
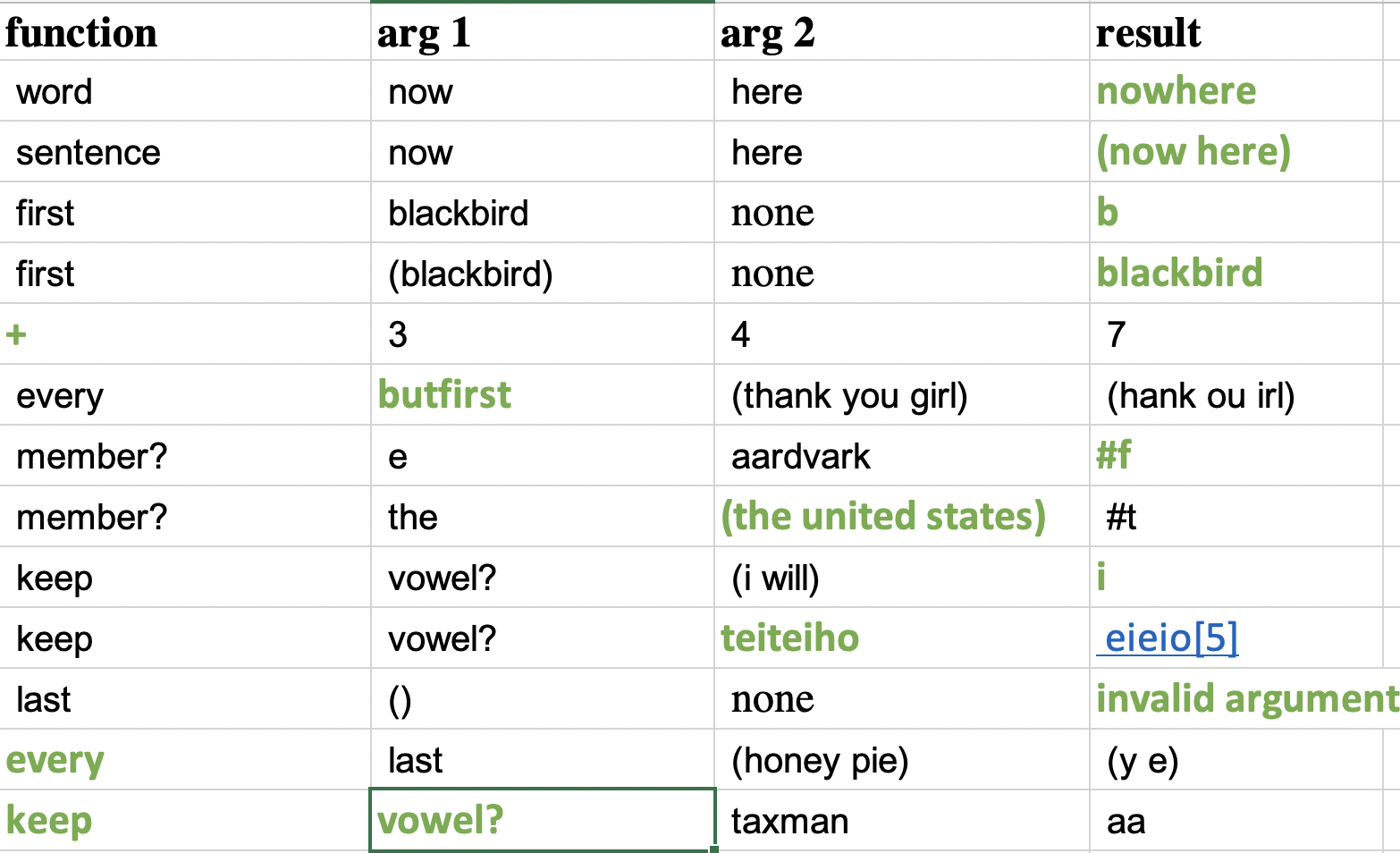
Exercise 2.2
2.2 What is the domain of the vowel? function?
vowel? accepts words, sentences, booleans, functions, and numbers as arguments (in the sense that it won’t reject these as outside its domain). Its range is a boolean value – it returns true if you give it a single letter vowel, and false if you give it anything else.
AnneBfound a couple of examples of things outside vowel‘s domain.
Exercise 2.3
2.3 One of the functions you can use is called
appearances. Experiment with it, and then describe fully its domain and range, and what it does. (Make sure to try lots of cases. Hint: Think about its name.)
Note: Correction below
appearances takes two arguments and appears to return the number of times that the first argument appears in the second argument if the first argument is a single digit letter, number, or punctuation mark.
If the first argument is a multi-character sequence, appearance returns zero, regardless of whether or not the sequence provided as the first argument appears in the second argument.
appearances says that sentences are outside its domain but that may be related to the technical issue described earlier. appearances will accept sentences as arguments in normal Scheme but does not appear to actually function as you might guess it would on sentences, as it will return 0 (instead of 1) even if passed identical sentences for both arguments.
The domain appears to be sequences of alphanumeric characters and punctuation marks (which we can generalize as “words”), and the range is positive whole numbers.
Some tests:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
|
Function: appearances
Argument: 7
Argument: potato7potato7potato7
The result is: 3
Function: appearances
Argument: 34
Argument: potato34potato34potato34potato3
The result is: 0
Function: appearances
Argument: 343434
Argument: 343434
The result is: 0
Function: appearances
Argument: 34
Argument: 3434
The result is: 0
Function: appearances
Argument: 9
Argument: 89989
The result is: 3
Function: appearances
Argument: 9
Argument: potato9potato9potato9
The result is: 3
Function: appearances
Argument: 7
Argument: wordword7word
The result is: 1
Function: appearances
Argument: p
Argument: pppp
The result is: 4
Function: appearances
Argument: '
Argument: '''
The result is: 3
Function: appearances
Argument: ''
Argument: ''''
The result is: 0
Function: appearances
Argument: ()
Argument: ()
Argument(s) not in domain.
Function: appearances
Argument: (potato)
Argument: (potato)
Argument(s) not in domain.
Function: appearances
Argument: 1.2
Argument: 1.2
The result is: 0
Function: appearances
Argument: 1/3
Argument: 1/3
The result is: 0
|
CORRECTION: AnneB shows that appearances takes sentences as the second argument if the first argument is a single character, and will find instances of the first argument in a sentence provided as the second argument, e.g.:
|
1
2
3
4
5
6
7
8
9
10
|
Function: appearances
Argument: d
Argument: (d d)
The result is: 2
Function: appearances
Argument: d
Argument: (dd d)
The result is: 1
|
I thought this example was interesting. appearances seems to work differently on sentences than on words. With words, it will count each instance of a character separately within a word. With sentences, appearances seems to want the characters to be spaced apart in order to register them as being an appearance.
|
1
2
3
4
5
6
7
8
9
10
11
12
|
Function: appearances
Argument: a
Argument: potato
The result is: 1
Function: appearances
Argument: a
Argument: (potato)
The result is: 0
|
So even if the same letter appears twice in a row in a sentence, it won’t count that, but it will count letters on their own:
|
1
2
3
4
5
6
|
Function: appearances
Argument: d
Argument: (d d d d d)
The result is: 5
|
|
1
2
3
4
5
6
7
8
9
10
11
12
|
Function: appearances
Argument: a
Argument: (a ah a ah a potato)
The result is: 3
Function: appearances
Argument: d
Argument: dd
The result is: 2
|
So a more correct statement is that appearances takes sequences of letters, numbers, and punctuation marks for the first argument, and all that plus sentences for the second argument, and returns a positive integer.
Exercise 2.4
One of the functions you can use is called
item. Experiment with it, and then describe fully its domain and range, and what it does.
What it does: After some testing (see below) it seems that item takes a number for the first argument, and a sentence or word (or a number treated as a word) as the second argument. Then it returns a character of the second argument, or word in the sentence, that corresponds to the number of the first argument. Specifically, it returns the character of the second argument or word in a sentence that you get if you start counting characters/words from the left side of the second argument until you get to the [first argument] character. For example, if the first argument is “3” and the second argument is “654”, then item will return the third character (counting from the left) of the second argument, which is 4. Or if the first argument is 5 and the second argument is Liberty, then item will return the fifth character of the second argument (counting from the left) which is r. Or if the first argument is “4” and the second argument is “(we the people of the united states)”, then item will return “of”.
Domain: the first argument has to a positive number less than or equal to the total number of characters (if a word) or words (if a sentence) of the second argument. The second argument has to be a word (including a number which is treated as a word) or sentence.
Some tests. Format is:
Arg1, Arg2: Result.
(I did a different format cuz i did tons of testing on this one, wanted it to be more compact)
0, 0: Argument(s) not in domain.
1, 0: 0.
2, 0: Argument(s) not in domain.
0, 1: Argument(s) not in domain.
0, 2: Argument(s) not in domain.
1, 0: 0.
1, 1: 1.
1, 2: 2.
1, 3: 3.
1, 4: 4.
1, 5: 5.
2, 0: Argument(s) not in domain.
2, 1: Argument(s) not in domain.
2, 2: Argument(s) not in domain.
2, 4: Argument(s) not in domain.
2, 23: 3.
2, 32: 2.
2, 33: 3.
2, 22: 2.
2, 57: 7.
2, 75: 5.
3, 654: 4.
3, 456: 6.
1, 456: 4.
2, 456: 5.
-1, -1: Argument(s) not in domain.
w, ww: Argument(s) not in domain.
15, 12345678901234567890: 5.
9, 123456789012: 9.
4, potato: a.
5, Liberty: r.
1, (grilled cheese and tomato sammich): Argument(s) not in domain. This appears to be an issue with functions.scm
0, potato: Argument(s) not in domain.
1, potato: p.
-1, potato: Argument(s) not in domain.
the ability to handle sentences as arguments is broken in functions.scm, as mentioned before. However, I tried the regular Scheme version of item to test how it handles sentences:
1, (potato tomato): potato.
2, (potato tomato): tomato.
Note for Exercises 2.5 through 2.9
The following exercises ask for functions that meet certain criteria. For your convenience, here are the functions in this chapter: +, -, /, \<=, \<, =, >=, >, and, appearances, butfirst, butlast, cos, count, equal?, every, even?, expt, first, if, item, keep, last, max, member?, not, number?, number-of-arguments, odd?, or, quotient, random, remainder, round, sentence, sqrt, vowel?, and word.
number? does not appear to be defined in my functions.scm file.
I made a (somewhat incomplete) list of data types of various functions as an aid to answering the questions.
List of functions by number of arguments
This section lists functions by number of arguments permitted for the argument within the functions.scm file used for this chapter. I made these lists cuz it seemed like they would be useful for answering the questions that follow.
List of one-argument functions
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
|
butfirst
butlast
cos
count
even?
first
last
not
number-of-arguments
odd?
random
round
sqrt
vowel?
|
List of two-argument functions
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
|
+
-
/
<=
<
=
>=
>
and
appearances
equal?
every
expt
item
keep
max
member?
or
quotient
remainder
sentence
word
|
List of three-argument functions
|
1
2
|
if
|
Exercise 2.5
List the one-argument functions in this chapter for which the type of the return value is always different from the type of the argument.
-
counttakes numbers but i guess it doesn’t treat them as numbers but as a string of characters. so it treats “666” just like “aaa”. it returns numbers. so I thinkcountalways returns things with a type different than the type of argument it takes. -
even?only has integers in its domain and only returns boolean values, so it would count as an example of such a function. -
number-of-argumentsonly has functions within its domain and only returns positive integers. -
odd?only has integers in its domain and only returns boolean values, so it would count as an example of such a function.
Exercise 2.6
List the one-argument functions in this chapter for which the type of the return value is sometimes different from the type of the argument.
-
vowelaccepts boolean values as an argument and returns boolean values. So if you provide it a boolean value and it returns a boolean value, then the type of the argument and the type of the return are the same. OTOH, if you provide it with a letter or word and it returns a boolean value, then the data types are different. So they are sometimes different.
NOTE:
So there seems to be a big difference in answers between me and AnneB. I think this may be an issue of how we interpreted the question but let’s see. AnneB says:
The ones for which the type of the return value is sometimes different from the type of the argument are:
count can take a word as an argument and return a number.
This one I can see as arguable. count seems a bit tricky to me. It takes numbers but seems to deal with them as any other character, and not as numbers. I’m not quite sure how to think about that issue, so I’ll focus on what I regard as the less ambiguous cases.
even?, number?, odd? can take a number as an argument and return a boolean.
my number? was broken so we’ll leave that aside.
re: even? and odd?, I think I am reading the question as asking “Which one-argument functions have return values of a type that is sometimes different from the type of the argument, and sometimes not” and AnneB is perhaps reading it in a different way.
even? and odd? take only numbers but return only booleans. They never return the same value as they take. So I think they always return a value different from the type of argument, not only sometimes.
number-of-arguments can take a function as an argument and return a number.
Similar logic here as with even? and odd? – number-of-arguments only takes functions and always returns numbers. So it always returns a type different than the type that it accepts.
vowel? can take a word as an argument and return a boolean.
we agree that vowel? is an answer.
Exercise 2.7
Mathematicians sometimes use the term “operator” to mean a function of two arguments, both of the same type, that returns a result of the same type. Which of the functions you’ve seen in this chapter satisfy that definition?
I read this to be asking for a function that always returns a result of the same type as the two arguments.
|
1
2
3
4
5
6
7
8
9
10
11
|
+
-
/
and
expt
max
or
quotient
remainder
word
|
NOTE: AnneB’s list is almost the same as mine, except that I have expt in my list and she does not.
Exercise 2.8
An operator f is commutative if f(a,b)=f(b,a) for all possible arguments A and B. For example,
+is commutative, butwordisn’t. Which of the operators from Exercise 2.7 are commutative?
|
1
2
3
4
5
|
+
and
max
or
|
Exercise 2.9
An operator f is associative if f(f(a,b),c)=f(a,f(f(b,c)) for all possible arguments A, B, and C. For example, * is associative, but not /. Which of the operators from Exercise 2.7 are associative?
I made a table to help me figure out whether OR was associative
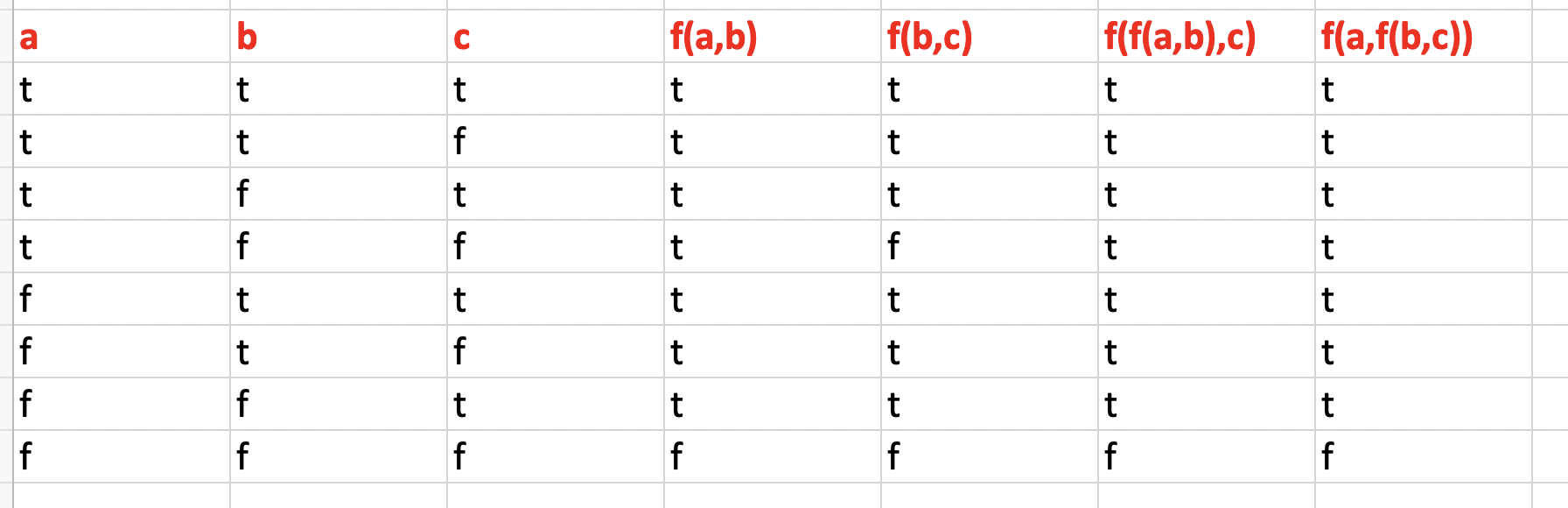
❌INCOMPLETE:
|
1
2
3
4
5
|
+
and
max
or
|
✅CORRECTION: AnneB lists word as associative and I think she is right. It does not matter whether you join words a and b first and then join ab with c, or join words b and c first and then join a with bc. The word order and result is going to come out the same in either case.
End of Chapter Review
Felt pretty solid on my development of the “testing things out” skill this chapter. I think that’s kind of the point of this chapter.
Trying to think somewhat rigorously about the domain and range of functions seems valuable.
Questions
What is the correct way to describe the domain of count, given that it takes numbers as arguments but treats them as words?
My Prior Learning Efforts
As with Chapter 1, there appear to be none to speak of.
Other People’s Learning Efforts
AnneB’s notes were super helpful to refer to. It’s hard to find much stuff to refer to for Chapter 2. You start seeing stuff for Chapter 3 and later.