This is how my initial definitions file looks like for this chapter:
|
1
2
3
4
5
6
|
#lang racket
(require "little_schemer.rkt")
(#%require racket/trace)
|
Note that with the (#%require racket/trace) line I can use trace 🙂
I’m requiring this file in order to deal with an issue described later.
Note that they specify for purposes of this chapter we’re focused on non-negative integers.
Commandments



Selected Portions of Exercises
+ (addition)
![]()
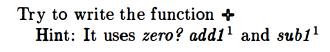
I named mine plus in order to avoid any issues with the existing + function:
|
1
2
3
4
5
6
7
|
(define plus
(lambda (a b)
(cond
((zero? b) a)
(else
(plus (add1 a)(sub1 b))))))
|
So basically, I recursively call plus while adding 1 to the first value and subtracting 1 from the second value until the second value is 0, at which point I return the first value. I kinda use the computer like an abacus that moves one bead at a time from b to a until b is zero, at which point a is returned.

This was their solution:

I found their approach slightly more complex than mine.
Basically what they do is add 1 to the result of calling their plus function with n and the result of running sub1 on m.
So suppose the initial values for n and m are 4 and 3. After you evaluate sub1 m, you have a 4 and a 2 to evaluate so that you can add 1 to them. When you try to evaluate that + with the 4 and 2, first you check whether m is equal to zero. Since it’s not, you have a further recursive call to +, this time with 4 and 1. This keeps going until you reach 4 and 0, and all the while, you are building up a recursive chain of add1‘s that are waiting to get evaluated.
When you get to the point where m is zero, you finally return 4 and can evaluate the chain of add1‘s you’ve built up:


Seems like these Commandments are going to have a lot of nuance 😉
– (subtraction)
My attempt at a subtraction function:
|
1
2
3
4
5
6
|
(define minus
(lambda (a b)
(cond
((zero? b) a)
(else (minus (sub1 a)(sub1 b))))))
|
I recursively call minus while subtracting 1 from each of a and b until b is zero, at which point I return a.

This is their solution:
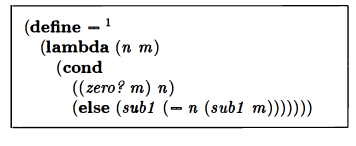
This works similarly to their addition function, in that they build up a chain of sub1‘s until the second value is 0. Then they evaluate their chain of sub1‘s using the first value.
I had some hesitancy around the idea of having two sub1‘s in the same expression. I think maybe I had an intuition that that’d be too much subtraction. But you need both for it to work. The first sub1, right after the else, becomes part of the chain of sub1‘s by which we reduce the first number. The second sub1, which actually gets evaluated as we go “down” in the steps of recursive calls, reduces the second number. If we didn’t reduce the second number as we tried to build up our chain of recursive calls, we’d get an infinite loop.
addtup (add a tup up)
A tup is a list of numbers. It includes the empty list. We can do operations on tups.


|
1
2
3
4
5
6
|
(define addtup
(lambda (tup)
(cond
((null? tup) 0)
(else (+ (car tup) (addtup (cdr tup)))))))
|
x (multiplication)

![]()
My answer:
|
1
2
3
4
5
|
(define x
(lambda (n m)
(cond ((zero? m) 0)
(else (+ n (x n (sub1 m)))))))
|
This method builds up a chain of (+ n... calls until m hits 0. Then we return 0. (x 3 0) is 0. But we add 0 to 3 and then keep moving up the chain of recursive calls until we’re done adding.


Good point. Equations are another way to think about recursive functions.
tup+ (combine tups)

For the initial version below, the tups have to be the same length. Thus the questions we need to worry about are (and (null? tup1)(null? tup2)) and else.
![]()
|
1
2
3
4
5
6
7
8
|
(define tup+
(lambda (tup1 tup2)
(cond
((and (null? tup1)(null? tup2)) '())
(else
(cons (+ (car tup1)(car tup2))
(tup+ (cdr tup1)(cdr tup2)))))))
|
The book then wants a variant that will work even if one tup is shorter than another.
|
1
2
3
4
5
6
7
8
9
10
|
(define tup+
(lambda (tup1 tup2)
(cond
((and (null? tup1)(null? tup2)) '())
((null? tup2) tup1)
((null? tup1) tup2)
(else
(cons (+ (car tup1)(car tup2))
(tup+ (cdr tup1)(cdr tup2)))))))
|
This works because, at the point one of the tups “runs out” of values, the entirety of the remaining part of the non-empty list is returned, without further use of car or cdr.
You can actually remove the ((and (null? tup1)(null? tup2)) '()) at this point. If both tups are the same length, then when null? tup2 goes to check if the second tuple is null, and it is null, then it’ll return the (also empty) tup1 as an empty list, which is what we want to return when both tups are null anyways…
|
1
2
3
4
5
6
7
8
9
|
(define tup+
(lambda (tup1 tup2)
(cond
((null? tup2) tup1)
((null? tup1) tup2)
(else
(cons (+ (car tup1)(car tup2))
(tup+ (cdr tup1)(cdr tup2)))))))
|
> (greater than)
The book calls this > but I used my own name
|
1
2
3
4
5
6
7
8
|
(define greaterthan
(lambda (n m)
(cond
((zero? n) #f)
((zero? m) #t)
(else (greaterthan (sub1 n) (sub1 m))))))
|
< (less than)
The procedure for < is pretty similar
|
1
2
3
4
5
6
7
|
(define lessthan
(lambda (n m)
(cond
((zero? m) #f)
((zero? n) #t)
(else (lessthan (sub1 n) (sub1 m))))))
|
If the second number is 0, and given that we’re not worrying about the possibility of negative numbers, then the first number has to be at least 0 as well, which would be a tie between m and n, not a case where n is less than m. (n could also be greater than m). So we’d return false. OTOH, if we know m isn’t zero, but n is zero, then that means n is less than m, so we return true.
= (equal)

My solution (I only used <):
|
1
2
3
4
5
6
|
(define equal
(lambda (n m)
(cond ((< m 1)(< n 1))
((< n 1) #f)
(else (equal (sub1 n)(sub1 m))))))
|
Given that we’re not worried about negative numbers, if m is less than 1 it has to be 0. If m is 0, then if n is also less than 1 (0), the function should return true. OTOH, if m is 0, but n is not 0, then the function should return false. That’s what happens with ((< m 1)(< n 1)). First we test for the value of m. Then if m is 0, we test for the value of n, and get true or false back depending on the value of n.
OTOH, if we get to the second cond clause, ((< n 1) #f), then we know that m isn’t 0. If we know that, and then we also know that n is less than 1 (so zero), then we know that n and m aren’t equal, and thus we should return false.
Otherwise we recurse.
Their solution is actually more straightforward. I think I was trying to follow the previous definition of = or something when I came up with mine:

But yeah. This solution kind of speaks for itself 🙂
↑ (exponents)
![]()

|
1
2
3
4
5
6
|
(define powerof
(lambda (n m)
(cond
((zero? m) 1)
(else (* n (powerof n (sub1 m)))))))
|
÷ (division)
This is how they do division

length (length of a list of atoms)


My answer, same as theirs:
|
1
2
3
4
5
6
|
(define length
(lambda (lat)
(cond
((null? lat) 0)
(else (add1 (length (cdr lat)))))))
|
pick (nth value of a list)
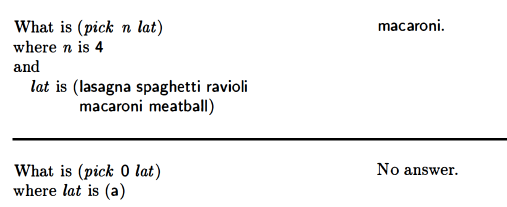

Mine was a little different than theirs:
|
1
2
3
4
5
|
(define pick
(lambda (n lat)
(cond ((= n 1) (car lat))
(else (pick (sub1 n)(cdr lat))))))
|
I used =. Seemed like fair game since it had been introduced.
Theirs was:

Totally valid solution, but I think ((zero? (sub1 n)) is a bit less straightforward than mine. I get that their version is compatible with the First Commandment though.
rempick (remove value from a list)

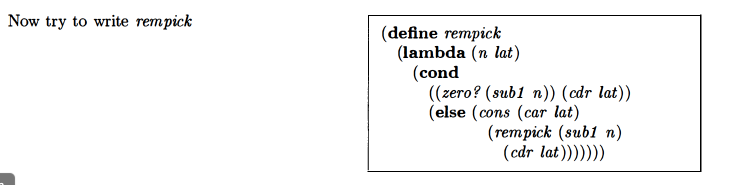
Mine was close, except I also had a null check for the lat:
|
1
2
3
4
5
6
7
|
(define rempick
(lambda (n lat)
(cond ((null? lat) '())
((zero? (sub1 n)) (cdr lat))
(else (cons (car lat) (rempick (sub1 n) (cdr lat))))
)))
|
I wasn’t sure whether the null? was necessary when I wrote it, I had the idea that it might come up when the n was out of range of the values in the lat.
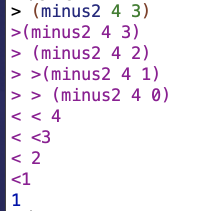
Trace results for my version:

And trace results for their version:

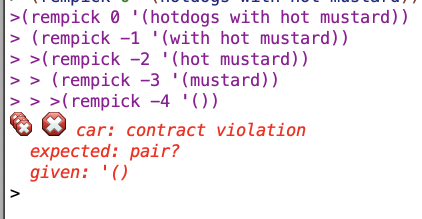
So basically for my version, if the n is out of range, the whole lat winds up getting returned, which I think makes sense (since the value you specified to remove is not in the range of the lat). Whereas with theirs you get an error message. I don’t think this is a huge deal but mine seems better.
no-nums (return everything but numbers)

My answer:
|
1
2
3
4
5
6
|
(define no-nums
(lambda (lat)
(cond ((null? lat) '())
((number? (car lat)) (no-nums (cdr lat)))
(else (cons (car lat) (no-nums (cdr lat)))))))
|
Theirs was basically the same but they did the cond/else structure that they like:

all-nums (return only the numbers)
My answer, same as theirs:
|
1
2
3
4
5
6
|
(define all-nums
(lambda (lat)
(cond ((null? lat) '())
(else (cond ((number? (car lat)) (cons (car lat) (all-nums (cdr lat))))
(else (all-nums (cdr lat))))))))
|
eqan? (eq? for atoms and numbers)
This was my first attempt:
|
1
2
3
4
5
6
7
|
(define eqan?
(lambda (n m)
(cond ((and (number? n)(number? m))
(= n m))
(else (cond ((eq? n m) #t)
(else #f))))))
|
This is theirs:

The eq? in my Racket takes numeric arguments for eq?. Therefore, my procedure works to handle some input like (eqan? 3 'potato). When that gets to the ((eq? n m) part, it evaluates as true. Whereas with their version of eq?, if you tried to evaluate that I guess you would get an error. That’s why, after they test whether both a1 and a2 are numbers, they test whether either one is. And only after that test do they try to use eq?.
Also now that I think about it, I think the last line of my version may be redundant. Maybe it’s better as:
|
1
2
3
4
5
6
|
(define eqan?
(lambda (n m)
(cond ((and (number? n)(number? m))
(= n m))
(else (cond ((eq? n m) #t))))))
|
Anyways, it seems like I should get my functions on the same page as the Little Schemer definitions in order to avoid future confusion. So I’m now using this file to do so.

hurrah
occur (count occurrences)

Mine:
|
1
2
3
4
5
6
7
8
9
|
(define occur2
(lambda (a lat)
(cond
((null? lat) 0)
(else
(cond
((eqan? a (car lat))(add1 (occur2 a (cdr lat))))
(else (occur2 a (cdr lat))))))))
|
theirs is basically the same except they use eq? instead of eqan?.
one? (is the value 1?)
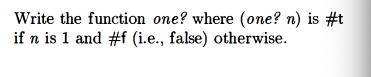
Mine:
|
1
2
3
4
5
|
(define myone?
(lambda (n)
(cond ((number? n)(= n 1))
(else #f))))
|
Their two options:

My version handles non-numbers without an error message cuz of the check for number?.

If you’re not worried about non-numeric input, you could do:
|
1
2
3
4
|
(define myone?
(lambda (n)
(= n 1)))
|
They agree.
rempick rewrite

My answer:
|
1
2
3
4
5
6
|
(define rempick
(lambda (n lat)
(cond ((one? n) (cdr lat))
(else (cons (car lat) (rempick (sub1 n) (cdr lat))))
)))
|
Their answer was the same.