The Little Schemer Chapters 2 & 3

I started making my own flash cards for exercises that I had doubts about or got wrong. I’m making them using the Mochi app, which you can easily paste images and markdown text into. I looked at the flashcards I mentioned in my last post but they seemed pretty minimal so I decided to make my own.

I didn’t have a lot to say about Chapter 2 since it was mostly about going through a chain of recursive calls with some specific examples and I followed it easily.

Oh, one thing I’m not sure I mentioned last time is that you’ve got to quote lists and words with either the (quote) function or the abbreviation ' for them to be recognized properly as data by DrRacket.

I’m only discussing some of the book content – in particular the parts that I had to think about more or made mistakes on – which is why I describe the stuff below as “Selected” exercises. If you actually go through the book, you will get a better idea of their method of asking tons of questions and going very step by step. Don’t be misled by the parts I’m posting here.

Chapter 2 – Do It Again

I found another The Little Schemer github. In it, I found how to define a function introduced in this chapter – the (lat?) function. I wanted to test my guesses. But it turns out figuring out how to define lat? is an exercise early on in the chapter. Whoops, spoiler! Anyways the lat? from that github is:

You can see that lat? recursively goes through a list, checking 1) if the list is null? in which case it returns true, or 2) checking if the car of the list is an atom, in which case it recursively calls lat? with cdr of the list, or 3) else returns false.

The style is a bit different than I am used to. But as was discussed in Simply Scheme Chapter 9, define‘s basic function is to give a name to some value as in (define pi 3.141592654). When we write something like define (square x) (* x x)) this is actually shorthand for (define square (lambda (x) (* x x))). That said, it’s shorthand I’ve been using constantly so it’s a bit weird to see things written out all the way.

Anyways I’d write lat? as:

Commandments

Well that’s pretty absolute.

Selected Exercises

I don’t think I’d thought of else as being a question that asks if else is true. I thought of it more as a fallback if all the other questions asked by a cond turn out to be false.

---

Chapter 3 – Cons the Magnificent

Commandments

Selected Exercises

rember

rember is a procedure that removes the first instance of an atom in a list.

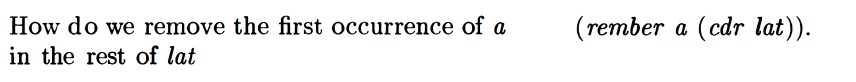
This makes sense but wasn’t immediately intuitively obvious to me for some reason. Since (rember a lat) removes the first instance anywhere in list lat, (rember a (cdr lat)) will remove the first occurrence anywhere in the rest of the list.

The book takes a stab at defining the rember procedure. This is a mistaken definition:

How it works:

If lat is null? return the empty list. Otherwise, if (car lat) is equal to a, return the rest of the list (or in other words return (cdr lat).) Otherwise, call rember with a and (cdr lat). This works only if the member being removed is the first atom in the list:

This is the fixed version:

And this is a version that is further simplified:

(You could make it even shorter with if but they haven’t introduced if in this text yet).

I think they’re saying that the (fixed) initial version better corresponded to the structure of the argument or reasoning underlying it. In the previous version you first checked for null? lat, and if that wasn’t the case you checked something else, and if that wasn’t the case you checked something else.

firsts

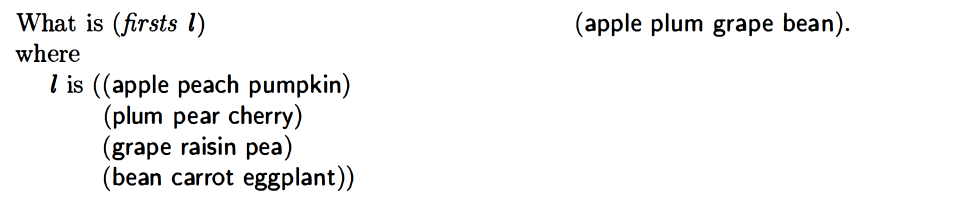
I got it after a couple of tries. At first I forgot to include else which resulted in returning an empty list, lol. Then I did (cons (car l)) instead of (cons (car (car l))), which just resulted returning the entire list of lists…

Anyways this was my working solution:

The book goes into a detailed discussion of firsts with the example (firsts '((a b)(c d)(e f)).

I thought this was good. It shows three different perspectives on what’s happening. Often you only think of one perspective. I think I mostly do something like either I or III, and do II way less.

insertR

My initial guess here was that it’d be ice cream with topping for dessert, but 1) that doesn’t make a ton of sense as a statement (like it’s replacing a more specific topping fudge with a vague topping) and also that’d be more of a replace and not an insert.

First occurrence is important qualifier. I left that out of my own description that I thought of mentally.

I tried to write the whole thing:

I needed to think about how to do the cons‘ing together of the old and new values with the remaining list. I also again weirdly omitted else the first time.

If car lat is equal to old, then….

(cons new (cdr lat))))

cons together the new value and the remainder of the list…

(cons (car lat) (cons new (cdr lat))))

…then cons the old value onto that new list.

Otherwise, cons the current car lat onto the value returned by a recursive call to insertR with cdr lat as the new lat.

I actually solved it differently than they wanted. I also didn’t follow the commandments. I’ll try doing it their way.

My new answer:

Their first attempt at an answer:

It gives erroneous output:

That’s because, while my version uses cons to combine all the relevant values together in the case where (eq? (car lat) old), they just return the rest of the list, which is insufficient to solve the problem. They go through a couple of steps to fix this – first trying to cons new onto cdr lat, and then separately trying to cons old onto (cons (cdr lat)). I like their method to approaching problems in general and this is a good example – they are very much trying to not skip steps.

insertL

I had some issues with making errors due to copy-pasting over some stuff from insertR to get started – like I accidentally left a recursive call to insertR in, heh. But I wound up with this:

Since we’re adding the new value to the left of the old value, things are actually simpler. We can just cons the new value onto the existing list once we determine that the old value is at the beginning of that list.

They recognize that you can solve the way I did but do a similar solution as before (with two cons invocations) but with flipping the new and old around.

subst

subst replaces the first occurrence of old with new. They want us to try writing such a procedure.

Here’s my answer:

subst2

Now they want something that replaces either the first occurrence of some old value o1 or the first occurrence of some old value o2 with a new value. My solution:

multirember

Now they want rember but where it removes all the instances of the value being removed. My solution:

After the null? check, we check if car lat is equal to a. If so, we recursively call multirember with cdr lat in the lat place. This effectively “skips over” the instance of a that is currently car lat. Otherwise, we cons together car lat with the value produced by calling multirember with cdr lat in the lat place. The cons‘ing effectively “retains” the value as opposed to skipping it.

multiinsertR

Now they want mutliinsertR. Here’s mine:

After the null? check, if we find that (car lat) is eq? to old, we cons the old value onto the cons of the new value and a recursive call to multiinsertR with (cdr lat) as the new lat. This consing inserts the new value and then we proceed to evaluate the rest of lat. Otherwise we cons the car of lat together with the value of a recursive call to multiinsertR with (cdr lat) as the new lat. This “saves” (car lat) as part of the resulting value of the procedure but does no insertion.

multiinsertL

The book asks if the following is correct:

At first glance it looked okay to me but I saw they said no so I looked closer. They forgot to do cdr lat on the first recursive call! They just did lat instead.

Here’s the correct answer:

mutlisubst

Now they want me to write multisubst:

Similar pattern as we’ve been seeing. After the null? check, if we find the old value we want to replace, we cons together the new value with the value produced by a recursive call to multisubst with (cdr lat) as the new lat. Otherwise, we cons together (car lat) with the value of mutlisubst with (cdr lat) as the new lat.