My work on http://people.eecs.berkeley.edu/~bh/ssch15/poker.html
The idea of this project is to invent a procedure
poker-valuethat works like this:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
|
> (poker-value '(h4 s4 c6 s6 c4))
(FULL HOUSE - FOURS OVER SIXES)
> (poker-value '(h7 s3 c5 c4 d6))
(SEVEN-HIGH STRAIGHT)
> (poker-value '(dq d10 dj da dk))
(ROYAL FLUSH - DIAMONDS)
> (poker-value '(da d6 d3 c9 h6))
(PAIR OF SIXES)
|
Counting The Distribution of Cards Among Suits
|
1
2
3
4
5
6
|
(define (count-suit suit hand)
(appearances suit (accumulate word hand)))
(define (count-suits hand)
(every (lambda (suit) (count-suit suit hand)) '(s h c d)) )
|
count-suits takes the hand as an argument. It returns a sentence of numbers representing the number of cards in a suit, with the digits of the sentence representing spades, hearts, clubs, and diamonds, respectively

count-suits uses count-suit to achieve its output. count-suit takes a suit and a hand as input and returns the number of times that suit appears in the hand.

|
1
2
3
4
5
6
7
8
|
(define (get-flush-suit suit-counts)
(cond ((= (first suit-counts) 5) 'spades)
((= (second suit-counts) 5) 'hearts)
((= (third suit-counts) 5) 'clubs)
((= (fourth suit-counts) 5) 'diamonds)
(else '())))
|
get-flush-suit takes the output of count-suits as an argument and returns the name of the suit if there is a flush, and an empty word otherwise.

|
1
2
3
|
(define (flush? flush-name)
(not (empty? flush-name)))
|
flush? takes the output of get-flush-suit as an input, and returns true if it’s not empty and false otherwise.
Counting the Number of Times a Rank Appears in a Hand
|
1
2
3
4
5
|
(define (compute-ranks hand)
(computed-ranks-to-sent
(compute-ranks-helper hand)
'(a 2 3 4 5 6 7 8 9 10 j q k)))
|
compute-ranks takes the hand as an argument and outputs a sentence containing the ranks that appear in that hand in the format of a spelled-out number representing the number of appearances followed by the rank (see image for example). compute-ranks invokes two procedures to help do the job.

|
1
2
3
4
|
(define (compute-ranks-helper hand)
(every (lambda (rank) (compute-rank rank hand))'(a 2 3 4 5 6 7 8 9 10 j q k)))
|
compute-ranks-helper takes the hand as an argument. Returns a sentence where the numbers in the sentence represent the number of times a hand rank appears in the hand, going from A to K. Uses an every and a lambda to go through the entire list of possible ranks.

|
1
2
3
|
(define (compute-rank rank handranks)
(appearances rank (accumulate word handranks)))
|
compute-rank takes a given rank and a hand as arguments, and returns the number of times that rank appears in the hand.
|
1
2
3
4
5
6
7
8
9
10
|
(define (computed-ranks-to-sent computed-ranks list-of-ranks)
(cond ((empty? list-of-ranks) '())
((equal? 0 (first computed-ranks)) (computed-ranks-to-sent (bf computed-ranks) (bf list-of-ranks)))
(else (se (num-to-word (first computed-ranks)) (first list-of-ranks)
(computed-ranks-to-sent (bf computed-ranks) (bf list-of-ranks))))))
(define (num-to-word num)
(item num '(one two three four)))
|
computed-ranks-to-senttakes a sentence representing the number of times a card rank appears in a hand and a list of hand ranks as arguments. It returns a sentence containing the ranks that appear in the format of a spelled-out number representing the number of appearances followed by the rank (see image for example)
Recursively goes through the computed-ranks and list-of-ranks. The list of ranks being empty is the base case. Hand ranks that have 0 appearances in the hand are skipped over. Otherwise, num-to-word is invoked to turn the number of appearances into a word, and that is combined with the rank into a sentence, and the procedure is recursively called again.

|
1
2
3
4
5
6
7
8
|
(define (computed-ranks-names number computed-ranks)
(cond
((empty? computed-ranks) '())
((equal? number (first computed-ranks))
(se (card-rank-to-name (second computed-ranks))
(computed-ranks-names number (bf (bf computed-ranks)))))
(else (se (computed-ranks-names number (bf (bf computed-ranks)))))))
|
computed-ranks-names takes a spelled-out-number representing the number of instances a rank appears in a hand and the results of running compute-ranks on a hand as arguments. Returns sentence containing the spelled-out-name of the rank or ranks that appear a given number of instances. This is a recursive procedure in order to be able to handle the case of having a hand with two pairs – in that case, cards of different ranks (fours and sixes, for example) appear twice in the hand.

I followed the SS book’s suggestion about how to format the output of compute-ranks. It’s important to keep in mind that the output of computed-ranks-names is the spelled out names of the rank you are searching for. So e.g. if you give it 'one as the first argument, you’re looking for one in the hand. If computed-ranks-names finds one 3 in the hand, as in the last example in the above image, the procedure will output three. It takes the 3 and turns it into a three using card-rank-to-name. Given that the initial data structure is a spelled out number representing instances followed by a numeric number representing hand rank, and we’re taking that and spelling out the rank for a given number of instances, it could get confusing, so I wanted to write this note about what’s going on.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
|
(define (card-rank-to-name letter)
(cond ((member? letter '(a 1 14)) 'ace)
((equal? letter '2) 'two)
((equal? letter '3) 'three)
((equal? letter '4) 'four)
((equal? letter '5) 'five)
((equal? letter '6) 'six)
((equal? letter '7) 'seven)
((equal? letter '8) 'eight)
((equal? letter '9) 'nine)
((equal? letter '10) 'ten)
((member? letter '(j 11)) 'jack)
((member? letter '(q 12)) 'queen)
((member? letter '(k 13)) 'king)
(else 'idk)))
|
card-rank-to-name converts a card rank to a spelled out name. pretty straightforward. I don’t think the need for converting A-J-K-Q straight from letters to words actually arises in my program, but I decided to include it when I wrote this cuz it seemed trivial to do so.
Finding Straights
|
1
2
3
|
(define (sort-ranks hand)
(sort (convert-all-ranks (hand-ranks hand))))
|
sort takes a hand as input and returns a sentence consisting of the ranks converted to numbers and sorted from least to greatest. aces are represented by two numbers – 1 and 14 – in order to represent the two ways in which they might form a straight in a given hand.

Here’s sort, and its support procedures. sort is for sorting numbers from least to greatest. It is based on some work from an earlier chapter:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
|
(define (before-num? num1 num2)
(< num1 num2))
(define (remove-once wd sent)
(cond ((empty? sent) '())
((equal? wd (first sent)) (bf sent))
(else (se (first sent) (remove-once wd (bf sent))))))
(define (earliest-helper so-far rest)
; so-far refers to the earliest word at this point in our analysis
(cond ((empty? rest) so-far)
; if rest is empty, that means so-far was earliest word in sentence, so we should return it
((before-num? so-far (first rest))
(earliest-helper so-far (bf rest)))
(else (earliest-helper (first rest) (bf rest)))))
(define (earliest-word sent)
(earliest-helper (first sent) (bf sent)))
(define (sort sent)
(if (empty? sent)
'()
(se (earliest-word sent)
(sort (remove-once (earliest-word sent) sent)))))
|

|
1
2
3
|
(define (convert-all-ranks ranks)
(every convert-rank ranks))
|
convert-all-ranks takes a sentence of hand ranks as input and returns a sentence of numbers. It converts any non-numeric ranks to numbers and converts aces to both 1 and 14.

|
1
2
3
4
5
6
7
|
(define (convert-rank rank)
(cond ((equal? rank 'a) '(1 14))
((equal? rank 'k) 13)
((equal? rank 'q) 12)
((equal? rank 'j) 11)
(else rank)))
|
convert-rank takes a card rank as input. Returns a number representing the rank if the rank is non-numeric and returns the same rank if it is numeric. Returns 1 and 14 for aces.

|
1
2
3
|
(define (hand-ranks hand)
(se (every (lambda (card) (bf card)) hand)))
|
hand-ranks takes the hand as an argument and returns the ranks by calling butfirst on each card within the hand

|
1
2
3
4
5
6
|
(define (straight? sorted-ranks) ;semipredicate
(cond ((< (count sorted-ranks) 5) #f)
((five-in-a-row? ((repeated bl (- (count sorted-ranks) 5)) sorted-ranks))
((repeated bl (- (count sorted-ranks) 5)) sorted-ranks))
(else (straight? (bf sorted-ranks)))))
|
straight? takes a sorted ranking of hands as input, and returns the values that represent the subset that constitutes a straight. The values that represent a straight are not necessarily the same as identical to the hand because of how I handle aces (i.e. by giving them two values).
If the number of value in the sorted ranking of hands drops below 5, the procedure returns false, as at that point the procedure will be unable to find five values in a row to form a straight.
If the subprocedure five-in-a-row? returns true, the straight? procedure will return the (true) value of the straight hand.
Otherwise, the straight? procedure is recursively called with all but the first value of the sorted ranks.

|
1
2
3
4
5
6
7
|
(define (five-in-a-row? five-cards)
(= (item 1 five-cards)
(- (item 2 five-cards) 1)
(- (item 3 five-cards) 2)
(- (item 4 five-cards) 3)
(- (item 5 five-cards) 4)))
|
five-in-a-row? a sentence consisting of five card rankings and returns true if the five cards increase by 1 from the first card to the last (indicating a straight).

Royal Flushes and Full Houses
|
1
2
3
4
5
6
7
8
|
(define (broadway? sorted-ranks)
(and
(equal? (last sorted-ranks) 14)
(equal? (last (bl sorted-ranks)) 13)
(equal? (last (bl (bl sorted-ranks))) 12)
(equal? (last (bl (bl (bl sorted-ranks)))) 11)
(equal? (last (bl (bl (bl (bl sorted-ranks))))) 10)))
|
broadway? takes the sorted numerical hand ranks as an argument and checks whether the final five values in sorted-ranks are the ranks for 10-J-Q-K-A. Returns true if so or false otherwise. This is part of the test for finding a royal flush.

|
1
2
3
4
|
(define (full-house? 3cards 2cards)
(and (not (empty? 3cards))
(not (empty? 2cards))))
|
full-house? takes sentences containing the names of the ranks for which there are 3 cards and 2 cards present in the hand, respectively. If such ranks exist (i.e. if a full house exists within the hand), full-house? returns true. Otherwise, it returns false.
|
1
2
3
|
(define (highcard straight)
(word (card-rank-to-name (last straight)) '-high))
|
highcard takes a sentence with the hand ranks within a hand that represent a straight as an argument. Returns the spelled-out rank of the high card within the straight with “-high” appended.

The Main Procedure
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
|
(define (poker-value hand)
(let ((sorted-ranks (sort-ranks hand))
(suit-counts (count-suits hand))
(computed-ranks (compute-ranks hand))
)
(let ((flush-suit (get-flush-suit suit-counts))
(4cards (computed-ranks-names 'four computed-ranks))
(3cards (computed-ranks-names 'three computed-ranks))
(2cards (computed-ranks-names 'two computed-ranks))
(straighthand (straight? sorted-ranks)))
(cond
((and (flush? flush-suit) ;royal flush
(broadway? sorted-ranks))
(se '(royal flush -) flush-suit))
((and (straight? sorted-ranks) ;straight flush
(flush? flush-suit))
(se (highcard straighthand)
'(straight flush)))
((equal? (count 4cards) 1) ;four-of-a-kind
(se '(four of a kind -) (pf 4cards)))
((full-house? 3cards 2cards) ;full house
(se '(full house -)
(pf 3cards)
'over
(pf 2cards)))
((flush? flush-suit);flush
(se '(flush - )
flush-suit))
((straight? sorted-ranks) ;straight
(se (highcard straighthand) 'straight))
((equal? (count 3cards) 1) ;three-of-a-kind
(se '(three of a kind -) (pf 3cards)))
((equal? (count 2cards) 2) ;two-pair
(se '(two pair - )
(se (pf 2cards)
'and
(plural (second 2cards))
)))
((equal? (count 2cards) 1) ;pair
(se '(pair of) (pf 2cards)))
(else '(nothing))))))
|
poker-value takes a sentence consisting of individual cards with suit and rank information as an argument, and returns ranking information about the hand.

Defining and Using Terms
Numerous values are defined in two sets of let expressions.
The first let:
-
sorted-ranksconsists of a sentence consisting of words of card hand ranks, without any suit information The purpose of sorted-ranks is to enable the detection of straights. -
suit-countsconsists of a sentence of numbers representing the number of cards in a suit, in the following order: spades, hearts, clubs, diamonds. The purpose of suit-counts is to enable the detection of flushes. -
computed-ranksis a sentence containing the ranks that appear in the format of a spelled-out number representing the number of appearances followed by the rank, e.g.(three 2 two q)for the result of(compute-ranks '(h2 c2 s2 dq hq)). The purpose of computed-ranks is to enable me to detect hand ranks that involve the presence of multiple cards of the same rank, such as full houses, x-of-a-kind, and pairs.
The second let:
-
flush-suitis a word containing the name of the suit of a flush, if a flush is present for a given hand. if a flush is not present, flush-suit will be an empty word -
4cardsis a sentence with the names of the hand rank within a hand for which there is four copies, if any. -
3cardsis a sentence with the names of the hand rank within a hand for which there are three copies, if any. -
2cardsis a sentence with the names of the hand ranks within a hand for which there are two copies, if any. -
straighthandis a sentence representing the hand ranks within a hand that represent a straight.
The structure of poker-value is a large cond with tests for particular hands arranged in order of the ranking of hands in poker.
- Royal flushes are tested for first, using a combination of
flush?andbroadway?. - Straight flushes are tested for using a combination of
straight?andflush?. - Fours-of-a-kind are tested for using for by checking that the
countof4cardsis equal to 1. -
full-house?tests for full houses in a similar manner as fours-of-a-kind, but this time checking the count of3cardsand2cards. - Flushes and straights are tested for using the
flush?andstraight?procedures, respectively. - threes-of-a-kind, two pairs, and pairs are tested for in a similar manner as to 4 of a kind, making the appropriate adjustments in terms of looking for the correct number of instances.
Helper Procedures
here are some general “helper” procedures I used. Note in particular pf, which comes up often and which is just a shorthand for calling plural on the first element of some input.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
|
(define (plural wd)
(cond
((equal? (word (last (bl wd))(last wd)) 'is)(word (bl (bl wd))'es))
((member? (word (last (bl wd))(last wd)) '(sh ch)) (word wd 'es))
((member? (word (last (bl wd))(last wd)) '(ay ey iy oy)) (word wd 's))
((equal? (last wd) 'y) (word (bl wd) 'ies))
((member? (last wd) '(s x z)) (word wd 'es))
(else (word wd 's))))
(define (pf sent)
(plural (first sent)))
(define (second input)
(first (bf input)))
(define (third input)
(first (bf (bf input))))
(define (fourth input)
(first (bf (bf (bf input)))))
|
Tree & Closing Thoughts
While I have generally pasted full programs in one place in my blog post, for this one I’m going to link to my github for the full program since it is pretty large.
Here’s a partial tree of my program:
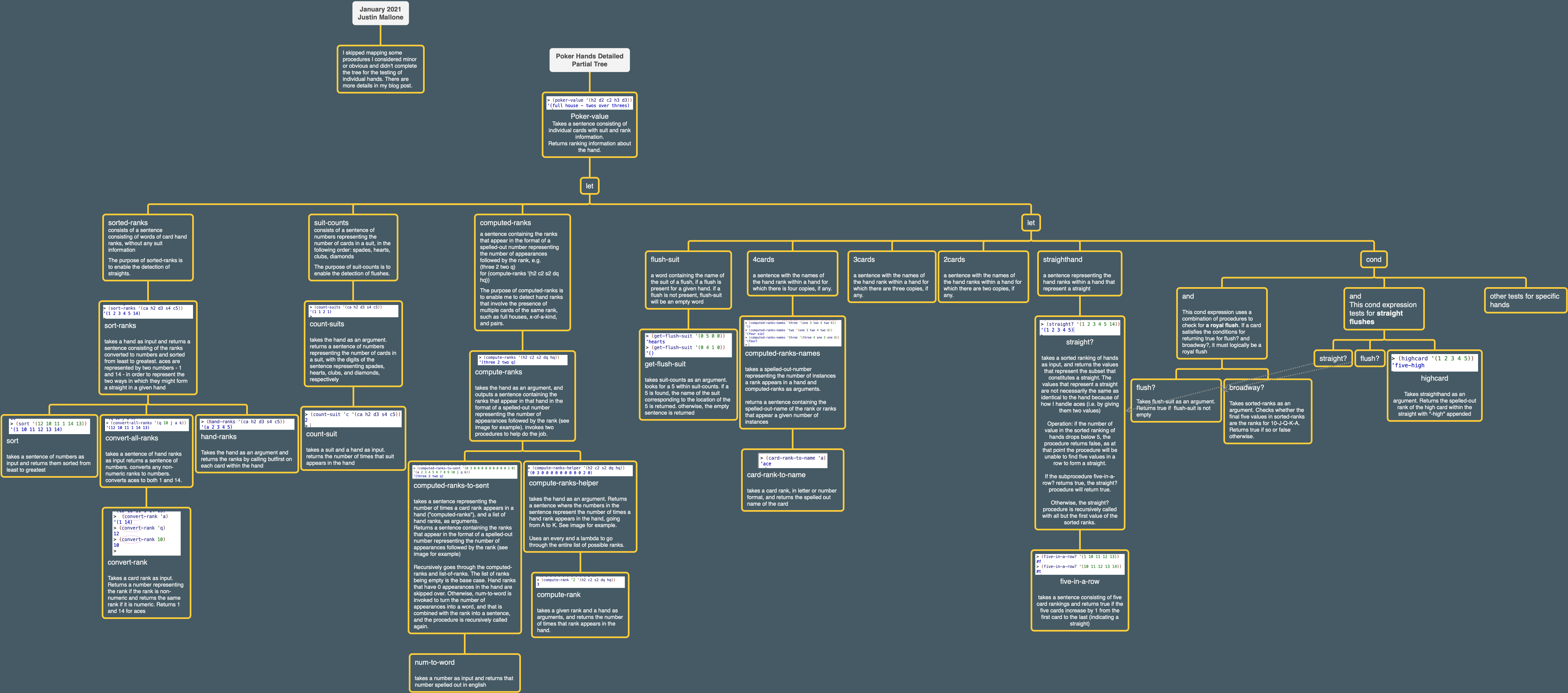
I’m skipping the “Extra Work for Hotshots” for now since I found the basic program challenging to write. One of the suggestions was to try scoring a 7 hand variant. I might try it later.
I don’t appear to have attempted the poker problem in previous Simply Scheme attempts. First time beating this level 🙂
I searched and only found one person who posted their poker hands project online, but it’s a 7 hands solution, and I don’t want to read it yet cuz I might want to try the 7 hands version later.
I thought this exercise was interesting. It caused me to mentally shift my focus a bit. Oftentimes I am just thinking about how to solve the problem in some “direct” way. With this exercise, I wound up thinking more in terms of “what format of data would be useful for solving the problem, and how do we generate the data in that format?” The book gave some guidance on that, but that was still “the hard part”. Once you had the data in the right format, actually finding the answers you want is pretty easy.
I first used the tree to help organize my program as I was writing it. I then translated my tree and program into this blog post. Both the tree-making stage and the writing stage led to me finding errors or problems which I then was able to correct. The step of writing out your thoughts explicitly helps error correct, and doing that in different formats helps you find different errors, since you notice different things. For example, the vertical structure of trees might help me figure out that the way i’m imagining data flowing through a process doesn’t make sense, while the linear format of writing might help me more with figuring out that I failed to update a procedure later in my program in light of an earlier change. So getting different angles and using different tools is useful.
There still may be errors cuz I didn’t really proofread.