Simply Scheme Chapter 13 – How Recursion Works

This chapter mostly reviewed the little people method but applied it to recursion, and also talked about trace. I didn’t find anything confusing or hard to follow so I’m going to skip straight to the exercises for this one.

Boring Exercises

✅ Exercise 13.1

Trace the explode procedure […] and invoke

This is the code they want you to use:

And this is the result:

How many recursive calls were there?

It occurs to me that I’m not sure whether the initial invocation of the procedure should be counted as a recursive call. I think maybe it only counts as a recursive call if the procedure is calling itself, and it doesn’t count as a recursive call to merely invoke a recursive procedure. Under that reasoning, there is the initial invocation of explode and three recursive calls. This is a different answer than if you ask the question (premised on the little person model of evaluating procedures) “How many explode specialists were involved in evaluating (explode 'ape)?”

What were the arguments to each recursive call?

1. the bf of ape (pe)
2. the bf of pe (e)
3. the bf of e (")

The final call hits the program’s base case, so no further calls are made.

Turn in a transcript showing the trace listing.

I basically did this already with my screenshot above.

✅ Exercise 13.2

How many pigl-specialist little people are involved in evaluating the following expression?

What are their arguments and return values, and to whom does each give her result?

pigl procedure for reference:

I think for the purposes of thinking of the little people model, you would want to include the first invocation of the recursive procedure. So my guess is there would be 4 little people involved here, because we wouldn’t get to the base case until the fourth letter.

1. piglspecialist Adam takes throughout and needs to hire someone to evaluate pigl with argument (word (bf 'throughout) (first 'throughout)) or (after a word specialist puts the results of bf and the first together) pigl hroughoutt
2. pigl specialist Bob takes hroughoutt and needs to hire someone to evaluate pigl with argument (word (bf hroughoutt) (first hroughoutt)) or (after a word specialist puts the results of bf and the first together) pigl roughoutth
3. pigl specialist Charlie takes roughoutth and needs to hire someone to evaluate pigl with argument (word (bf roughoutth) (first roughoutth)) or (after a word specialist puts the the results of bf and the first together) pigl oughoutthr
4. pigl specialist Donna takes oughoutthr and discovers she’s got the base case

And then being a recursive procedure things start again from the “bottom up”

1. Donna has a word specialist add ay to her oughoutthr, then returns the valueoughoutthray to Charlie.
2. Charlie returns the value oughoutthray to Bob.
3. Bob returns the value oughoutthray to Adam.

Let’s use trace again to confirm this story:

This seems consistent with what I said.

The throughout is transformed as it is being provided as an argument to each recursive call to pigl. Therefore, once it reaches the base case, it’s actually done being transformed, and just needs to be passed up along the chain, having already arrived at its final state in the base case. I think the lack of further transformations is why there isn’t the nesting that you see in 13.1.

I should add that at the end, Adam is the highest pigl person and reports to no one, and so at that point the value prints.

✅ Exercise 13.3

Here is our first version of downup from Chapter 11. It doesn’t work because it has no base case.

Explain what goes wrong to generate that error. In particular, why does Scheme try to take the butlast of an empty word?

downup keeps getting passed the bl of the initial word toe in each recursive call, going down to to and then t and then "". With no base case, downup tries to take bl of "", hence the error message.

You need something that tells downup to stop. In the case of downup specifically, for the functionality desired, you want the program to stop before it reaches the empty word. You want to stop when the word hits a length of 1.

✅ Exercise 13.4

Here is a Scheme procedure that never finishes its job:

Explain why it doesn’t give any result. (If you try to trace it, make sure you know how to make your version of Scheme stop what it’s doing and give you another prompt.)

It actually does finish its job in exactly one case – if you give it the argument 0. (Although really, a procedure named forever sounds like it has its job as never finishing, so maybe it succeeds at its job except when you give it 0 🙂 )

Otherwise, what happens is that you keep calling (+ 1 (forever [somenumber]. So if you use 5 as the argument, you get endless attempts to recursively call forever with 5. For the program to end, you’d need to change the value being passed in as the argument recursively. For example, if you did…

…then ultimately you wind up with a function that just adds 1 to whatever non-negative integer you put in it.

Real Exercises

✅ Exercise 13.5

It may seem strange that there is one little person per invocation of a procedure, instead of just one little person per procedure. For certain problems, the person-per-procedure model would work fine.
Consider, for example, this invocation of pigl:

Suppose there were only one pigl specialist in the computer, named Patricia. Alonzo hires Patricia and gives her the argument prawn. She sees that it doesn’t begin with a vowel, so she moves the first letter to the end, gets rawnp, and tries to pigl that. Again, it doesn’t begin with a vowel, so she moves another letter to the end and gets awnpr. That does begin with a vowel, so she adds an ay, returning awnpray to Alonzo.
Nevertheless, this revised little-people model doesn’t always work. Show how it fails to explain what happens in the evaluation of

With the revised little people model, pigl is easy to explain because “prawn” is being transformed as it is being passed in to each recursive invocation of pigl and then finally in the base case. pigl doesn’t follow a procedure model where you go all the way down to the base case and then work your way back up to the top, combining the results of each nested invocation until you get to a final result. pigl is instead more like an assembly line where one thing gets changed at each step.

In an assembly line, it can be way way more efficient to have a bunch of workers doing something, but it is easy to imagine one worker doing all the steps.

downup is different than pigl. It does follow a procedure model where you go all the way down to the base case and then work your way back up to the top, combining the results of each nested invocation until you get to a final result.

At the first step, when we’re dealing with smile, little person Anna knows that the “bookends” of the expression that gets returned will be smile, cuz that’s what she’s responsible for. But there’s this thing in the middle, (downup (bl 'smile)), that needs to get figured out. And I think maybe you could still imagine this as one little person but it is not as intuitive as with pigl. Like you can imagine that Anna starts her part of the procedure, dealing with smile, and then realizes she can’t go further until she figures out (downup (bl 'smile)). So then she switches tasks and tries to figure that out, and gets part of the way and figures out that she’ll have two smil‘s inside her two smile‘s, but then realizes she needs to figure out another step to move forward, and so on. In this model, what Anna is doing is less like an assembly line and more like switching tasks a bunch so she can move forward in her project.

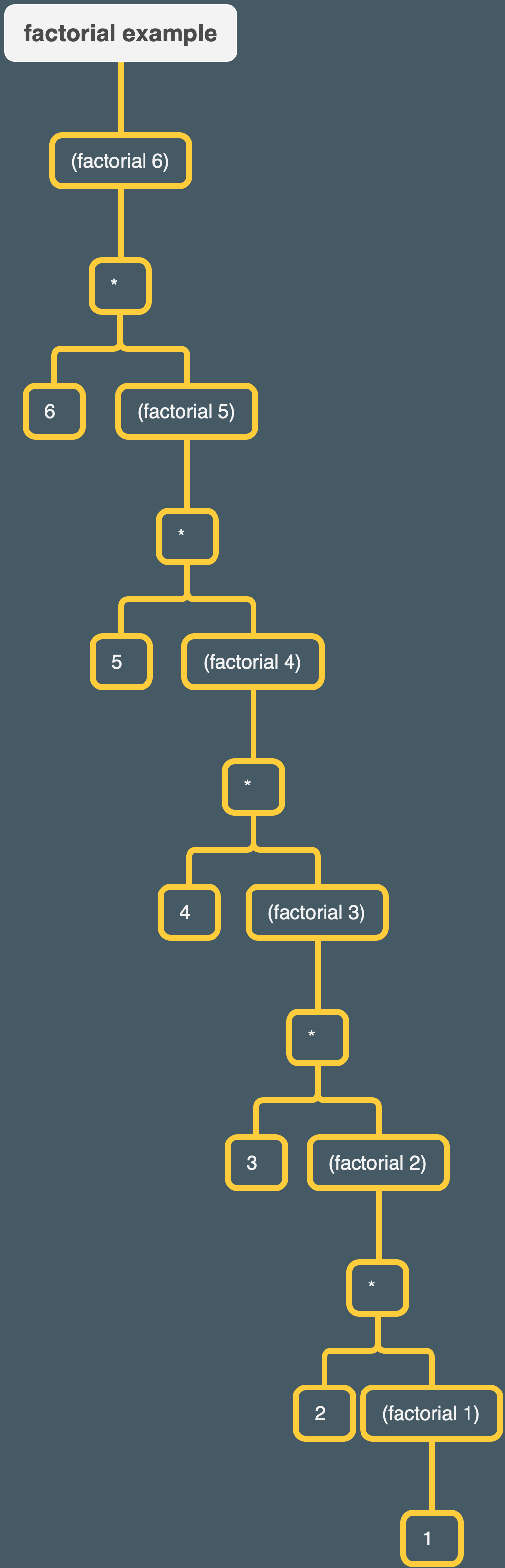
✅ Exercise 13.6

As part of computing (factorial 6), Scheme computes (factorial 2) and gets the answer 2. After Scheme gets that answer, how does it know what to do next?

The factorial program for reference:

I made a tree to help answer this. The structure is a bit of a hybrid – I kept factorial together with its argument, in order to help show the hierarchy and show what procedures “make up” a given invocation of factorial, but otherwise kept the structure standard, placing arguments to procedures as children underneath their procedure-parents:

To complete the evaluation of (factorial 2), Scheme needs to evaluate (factorial 1). It does so (returning 1 as our factorial program requires) and then proceeds to evaluate (factorial 2), returning (* 2 1). The same process repeats itself for (factorial 3). Scheme needed to know the answer to (factorial 2) in order to calculate (factorial 3). It temporarily put aside (factorial 3) in order to find the answer to (factorial 2), but the answer having been found, Scheme then proceeds to compute the answer.

So Scheme knows what to do next because the series of recursive invocations creates a nested tree structure in which the evaluation of a “lower level” of the recursive procedure (lower level meaning, in this case, an invocation of factorial with a smaller number closer to the base case of 1) is necessary for the evaluation of a “higher level” of the procedure. Scheme keeps track of this nested tree structure as it tries to evaluate each respective level of factorial. When the lowest level, the base case, is reached, Scheme can actually started to evaluate stuff. The evaluation then starts to “float up” the tree structure. E.g. getting the answer to the base case, (factorial 1), lets Scheme evaluate the answer to (factorial 2), and getting the answer from (factorial 2) lets Scheme evaluate (factorial 3) and so on.